一些三角函数的导数（如何直观地理解三角函数的导数）

作者 | 大小吴

来源 | 大小吴的数学课堂

学过高等数学的你是否还记得这两个式子

这里给出的是三角函数和的导数，今天大小吴就和大家来聊聊如何直观地理解它们。

我们知道，在微积分中导数是一个非常重要的概念，即函数的自变量在一点上产生一个增量时，函数值的增量与的比值在趋于0时的极限，记为

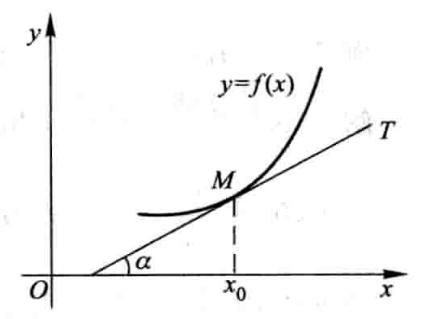
由上图也可以知道，当点无限趋近于点时，导数的几何意义便是函数所代表的曲线在点上的切线斜率。

通过导数的定义我们可以计算三角函数和的导数（以为例）：

根据两角和的正弦公式

代入以上极限，得到

由极限（证明略）

得到

即

这样我们就得到了的导数。

通过上述计算我们同样也可以得到的导数，但是你一定不想再来一遍了——因为整个过程略显繁琐与复杂。

那就让我们换一个角度——通过几何直观来看看到底什么是和的导数。

现在我们构造一个直角三角形，使其斜边长：

设其中一个锐角为，则两条直角边分别为、.

别忘了，现在我们要求的是和的导数，回忆一下导数的定义是什么，求导数需要什么？

是的，我们需要微小的增量！然后再看看和会发生什么变化。

对于角度，如果有一个微小的增量，会发生什么？想象一下（如果你想好了，就可以滑动图片查看）

<<< 左右滑动见更多 >>>

在研究函数曲线的导数时，我们可以将某一部分进行“无限放大”，从而达到“以直代曲”的目的。

同样地，在这里我们也可以对直角三角形进行无限放大，看看会发生什么（这里也可以想象一下，然后看看是否和你想得一样）。

<<< 左右滑动见更多 >>>

如果增加的角度无限趋近于0（这时记为无穷小量），则不难想象直角三角形的新的斜边与原来的斜边是无限接近平行的，如果我们在无限放大的地方再构造一个直角三角形，会得到如下图形：

我们发现，无限放大处的直角三角形和原来的直角三角形是相似的！又由于原直角三角形斜边长为1，因此我们可以认为放大处的直角三角形斜边即为，则两条直角边即为和.

因此，对于原来的直角边来说，其增量是，对于原来的直角边来说，其增量是.

因此，根据导数的定义，得到

参考文献

[1]（美）阿德里安·班纳.普林斯顿微积分读本（修订版）[M].杨爽等译.人民邮电出版社，2020.[2]（美）杰森·威尔克斯.烧掉数学书[M].唐璐译.湖南科学技术出版社，2020.