口袋妖怪什么属性最烂（口袋妖怪谁最强）

日前，Pokemon 的最新作品《Pokémon LEGENDS Arceus》发售。 在新型口袋妖怪 佐鲁亚 和 佐罗亚克 备受关注。 出乎意料的是，这两种类型都是从未出现过的 普通幽灵 。

知道《口袋妖怪》的人就不用解释了，不过这是普通类型的一个很弱的地方，禁用与鬼系的战斗技，同时禁用鬼系的鬼技，也就是鬼系的弱点，用普通型，平衡的，梦幻般的复杂型。 传闻这个 普通幽灵 可能是最强组合。

但真的是这样吗？

口袋妖怪类型相似性

口袋妖怪一共有18种，一个口袋妖怪最多可以有两种。另一方面，口袋妖怪的技能也分配了一种类型。防御口袋妖怪的伤害倍数由“使用的技术类型”和“自己的类型”的兼容性决定。

类型之间的兼容性如下图所示。

只要你玩过日本的游戏基本都知道，○表示 效果极好！ （伤害翻倍），△表示 效果不好 （伤害为0.5倍），×表示 无效果 （伤害为0倍）。不是的部分是正常效果（伤害为1倍）。拥有两种类型（复合类型）的口袋妖怪受到的伤害是由两种类型的兼容性的乘积决定的。比如草系技的伤害是2×2=4倍，水系技的伤害是0.5×2=1倍，电系技的伤害是针对“水/地”系的口袋妖怪。是 2 × 0 = 0 。

类型的另一个重要规范是 类型匹配 的概念。这意味着如果口袋妖怪使用与自己相同类型的技能，它的力量将是正常的 1.5 倍。这意味着电气型口袋妖怪释放的 10 まんボルト 普通型口袋妖怪释放的 10 まんボルト 更强。

这就是你需要知道的关于口袋妖怪战斗的全部内容。将根据这些事实进行计算。相反，关于口袋妖怪的知识将不再出现在分析阶段。也就是说，纯粹类型的实力在给出答案之前是不考虑的，比如那种类型的口袋妖怪究竟存在什么样的特性和种族价值观，什么样的技术流行或者更优秀。

类型间兼容性的制定

首先，让我们为 18 种类型中的每一种分配一个从 1 到 18 的数字。这允许口袋妖怪的类型由 (x, y) 和两个数字的组合表示。另外，如果口袋妖怪只有一种类型，我们将使用 0 编写 (0, x)，表示“无”类型。

在这里，使用的类型 x 技术对抗类型 (0, y) 口袋妖怪时的伤害乘数米xy _米x x是的会做。这对应于上一节中提到的“兼容性矩阵”的 x-by-column 分量的放大倍数。

首先要进行数据的归一化处理，此时释放x型技能对(y,z)型口袋妖怪的伤害比是f(x,(y,z))是

此外，考虑一个类型（w，x）的口袋妖怪可以对一个类型（y，z）的口袋妖怪造成多少伤害乘数。现在，type (w, x) Pokemon 将只使用其类型中包含的技巧类型（即可以通过类型匹配释放的技巧）。假设你选择了对对手更有效的技术类型，那么此时的伤害乘数就是综合伤害乘数。G( ( w , x ) 是

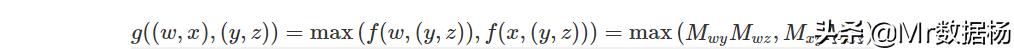
尝试计算（水，电）的（地，钢）的综合伤害率。水式技法是2×1=2，电式技法是0×1=0，所以大的“2”就是g的值。

但是，不能说（水、电）对（地、钢）有利。现在考虑（地、钢）的（水、电）的综合伤害乘数。地面型技术翻倍，钢型技术为0.5倍，g值也为2。也就是说，两人处于一种可以直面对方弱点的关系中，不能说谁更强。基于此，似乎可以通过组合损伤比之间的大小关系来确定复合类型之间的优劣关系。

目前，组合伤害乘数有多少 6 个可能的值：0,0.25,0.5,1,2,4。计算攻防切换时的综合伤害乘数，根据6个阶段相差多少来确定(w,x)相对于(y,z)的优势。从 -5 到 5 有 11 个可能的值，如果这是正值，则有利，如果是负值，则不利。

现在让我们考虑一下（水，电）相对于（火，岩石）的优势。g ((water,electric), (fire, rock)) 是“4”，因为它有四倍于水系的弱点，而 g ((water,rock), (water,electric)) ) 是“1”，因为岩石术造成的伤害是最大的。所以h的值是2-0=2，（水，电）相对于（火，岩）的优势是“2”（对应6个阶段的两次分离）。

实力对比来了

既然已经量化了类型之间的优劣关系，那么我们应该如何找到最强的类型呢？最简单的是计算相对于所有复杂类型的优势，并查看总值（分数）的大小。

包括“无”类型在内的 19 种类型中选择两种不同的类型进行统一的处理，并且创建兼容性矩阵 M。

types = ["無","ノーマル","ほのお","みず","でんき","くさ","こおり","かくとう","どく", "じめん","ひこう","エスパー","むし","いわ","ゴースト","ドラゴン","あく","はがね","フェアリー"] M =[[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0.5, 0, 1, 1, 0.5, 1], [1, 1, 0.5, 0.5, 1, 2, 2, 1, 1, 1, 1, 1, 2, 0.5, 1, 0.5, 1, 2, 1], [1, 1, 2, 0.5, 1, 0.5, 1, 1, 1, 2, 1, 1, 1, 2, 1, 0.5, 1, 1, 1], [1, 1, 1, 2, 0.5, 0.5, 1, 1, 1, 0, 2, 1, 1, 1, 1, 0.5, 1, 1, 1], [1, 1, 0.5, 2, 1, 0.5, 1, 1, 0.5, 2, 0.5, 1, 0.5, 2, 1, 0.5, 1, 0.5, 1], [1, 1, 0.5, 0.5, 1, 2, 0.5, 1, 1, 2, 2, 1, 1, 1, 1, 2, 1, 0.5, 1], [1, 2, 1, 1, 1, 1, 2, 1, 0.5, 1, 0.5, 0.5, 0.5, 2, 0, 1, 2, 2, 0.5], [1, 1, 1, 1, 1, 2, 1, 1, 0.5, 0.5, 1, 1, 1, 0.5, 0.5, 1, 1, 0, 2], [1, 1, 2, 1, 2, 0.5, 1, 1, 2, 1, 0, 1, 0.5, 2, 1, 1, 1, 2, 1], [1, 1, 1, 1, 0.5, 2, 1, 2, 1, 1, 1, 1, 2, 0.5, 1, 1, 1, 0.5, 1], [1, 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 0.5, 1, 1, 1, 1, 0, 0.5, 1], [1, 1, 0.5, 1, 1, 2, 1, 0.5, 0.5, 1, 0.5, 2, 1, 1, 0.5, 1, 2, 0.5, 0.5], [1, 1, 2, 1, 1, 1, 2, 0.5, 1, 0.5, 2, 1, 2, 1, 1, 1, 1, 0.5, 1], [1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 2, 1, 0.5, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 0.5, 0], [1, 1, 1, 1, 1, 1, 1, 0.5, 1, 1, 1, 2, 1, 1, 2, 1, 0.5, 1, 0.5], [1, 1, 0.5, 0.5, 0.5, 1, 2, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 0.5, 2], [1, 1, 0.5, 1, 1, 1, 1, 2, 0.5, 1, 1, 1, 1, 1, 1, 2, 2, 0.5, 1]]

基于此，将创建上面定义的函数 f、g、h。 例如，（水，电）对应（3,4），（火，岩石）对应（2,13）

import math import numpy as np def f(x,yz): y,z = yz return M[x][y]*M[x][z] def g(wx,yz): w, x = wx y, z = yz return max(f(w,(y,z)),f(x,(y,z))) def h(wx,yz): w, x = wx y, z = yz return int(np.round(math.log2(max(g((w,x),(y,z)),1/8))-math.log2(max(g((y,z),(w,x)),1/8))))

以简单的方式计算优势的总价值并输出排名。

result = [] for w in range(18): for x in range(w 1,19): score = 0 for y in range(18): for z in range(y 1,19): score = h((w,x),(y,z)) result.append(((w,x),score)) result.sort(key=lambda x:x[1],reverse=True) for i in range(171): wx,score = result[i] w,x = wx print(types[w],types[x],score)

top10 类型结果

じめん はがね 96 はがね フェアリー 92 ひこう はがね 90 ゴースト はがね 88 ほのお じめん 84 じめん ひこう 83 みず はがね 78 じめん フェアリー 72 かくとう はがね 71 ほのお はがね 67

前10名中有7种含钢，可见钢的卓越性。此外，排名第二的“钢铁仙子”属于“Zacian”，是使用率最高的最知名口袋妖怪之一，支持这种方法的有效性。

PageRank方法改进

这里出现了一个问题。用所有类型的优势总价值来确定最强者是否合适？即使你可以利用多种类型，但如果你只有没有出现在比赛中的弱类型对手，那也无济于事。反之，与所谓的强者进行战斗而不处于劣势的类型，可以说是真正的强者。

PageRank是一种根据网页的链接关系确定网页重要性的算法，是谷歌搜索引擎使用的技术。它不仅是从许多页面链接的重要，而且是通过考虑链接站点的重要性和链接数量来计算的。最好依靠图论的话来解释具体内容。

现在将每个网页视为一个顶点，将一个从一个页面到另一个页面的链接视为有向边的有向图，并让邻接矩阵为 A。此外，令 S 为通过将邻接矩阵的每一行除以每个顶点的度而获得的值。此时，S转置后的矩阵变成了转移概率矩阵，表示跟随链接的随机网上冲浪运动。

此外，在这里，我们将 Google 矩阵 G 定义如下。

α是一个称为阻尼因子的超参数，用于调整反向链接的重要性影响的大小。通常它似乎设置为 0.85。 T是瞬移矩阵，是一个方阵，其分量为“1/顶点数”。按顺序排列每个页面的重要性的向量λ，以下关系从重要性的递归定义中成立。

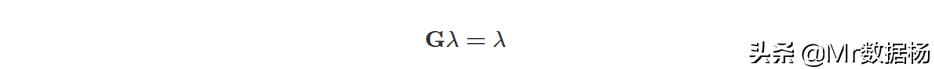
顺便一提，G也是一个转移概率矩阵（就像将每个顶点的重要性分配给链接的顶点），所以每一列的和都等于1。根据 Perron-Frobenius 定理，具有此类性质的非负矩阵“具有正特征向量，其未退化特征值为 1，并且没有更大的特征值”。

简而言之，G具有最大特征值的特征向量是我们想要的每个页面的重要性顺序。因此， PageRank 的简单而生动的主张是重要性的计算（假设特征值已知为 1）导致线性方程组的解。

最强的适配类型

在 PageRank，网站之间的链接被认为是定向的，并被用作确定其重要性的一个因素。另一方面，在口袋妖怪类型的情况下，这两种类型之间的关系已经在上一节的讨论中定量地理解了。然后，通过将每种类型放在顶点并将加权有向侧从劣势类型扩展到优势类型，就像指向“从我的角度来看这家伙很强大”（类似于链接）。我认为效果可期。

为简单起见，我们先用一个由火（ほのお）、水（みず）、地（じめん）和电（でんき）四种类型组成的图进行实验。

• 火 相对于 水 的优势是-2
• 火 相对于 地 的优势是-1
• 火 相对于 电 的优势是0
• 水 相对于 地 的优势是1
• 水 相对于 电 的优势是-1
• 地 相对于 电 的优势是 4

因此基于这些，从劣势到优势扩展“劣势程度”加权的一侧。如果优势为 0，则边不会被拉伸。

构建的加权邻接矩阵

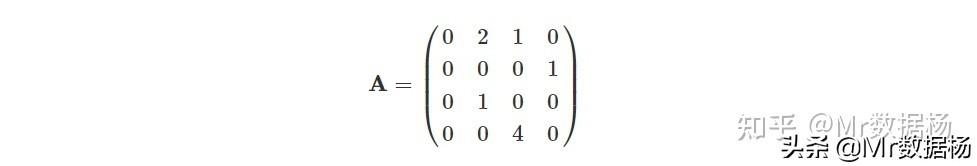
转移概率矩阵

根据公式计算的矩阵结果

使用 scipy 模块计算具有最大特征值的特征向量

from scipy.sparse.linalg import eigs S = np.array([[0,2/3,1/3,0],[0,0,0,1],[0,1,0,0],[0,0,1,0]]) T = 1/4*np.ones((4,4)) G = 0.85*S.T 0.15*T value, vector = eigs(G, 1) print(value, vector) >>>[1. 0.j] [[-0.06731985 0.j] [-0.58967561 0.j] [-0.5696563 0.j] [-0.56854412 0.j]]

由于特征向量的所有分量都是负数，所以第二个分量最大，稍有不同后，第三个和第四个分量几乎是相同的值，然后看起来第一个分量被大大分开后继续存在。这表示 水 > 地 ≒ 电 > 火，而 火 距离 水 、 地 、电 三个平衡点只有一步之遥。

如果类型数为4，则不会出现加权的含义，但如果增加边数，它肯定会起作用。

让我们对所有 171 种类型做同样的事情。就是做一个遍历循环而已。

d ={} # 对应数字字典 d_inv = {} k = 0 for i in range(18): for j in range(i 1,19): d[(i,j)] = k d_inv[k] = (i,j) k = 1 A = [[0 for _ in range(171)] for _ in range(171)] for w in range(18): for x in range(w 1,19): k = d[(w,x)] for y in range(18): for z in range(y 1,19): l = d[(y,z)] if h((w,x),(y,z)) < 0: A[k][l] = -h((w,x),(y,z)) A = np.array(A,dtype=np.float) S = np.zeros((171,171)) for i in range(171): S[i] = A[i]/sum(A[i]) T = (1/171)*np.ones((171,171)) G = 0.85*S.T 0.15*T value, vector = eigs(G, 1) vector = np.abs(vector.real) result = [] for i in range(171): w,x = d_inv[i] result.append(((w,x),vector[i][0])) result.sort(key=lambda x:x[1],reverse=True) for i in range(171): wx,score = result[i] w,x = wx print(types[w],types[x],score)

top10 类型结果

みず じめん 0.12901610166092206 じめん ひこう 0.12333336303638766 ほのお じめん 0.1230335213682247 じめん はがね 0.12253193098002743 ほのお はがね 0.11962533181338252 でんき はがね 0.11808330879585195 ひこう はがね 0.11638423434901143 はがね フェアリー 0.11133780309618507 みず フェアリー 0.11083098136702635 くさ はがね 0.11081844379517954

强大的钢铁之力依旧强大，只是后退了一点，而能够利用钢铁之力的弱点来代替它的地面部队，正在飞跃。从这种趋势的变化来看，类似PageRank的算法似乎在发挥作用，正如预期的那样，体现了“能对抗强类型的类型才是真正的强”。

让我们将其与最新的口袋妖怪使用率排名（2022/02/06）进行比较。

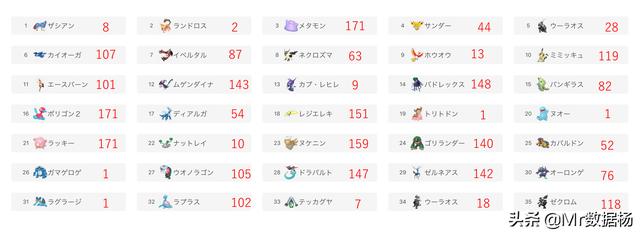
最终得出的结论 最强的口袋妖怪类型是 水/地 。

数据参考网站：https://www.pokemon.co.jp/ex/sun_moon/fight/161215_01.html 如果打不开请那个啥你们懂的。

,