几何辅助线和几何模型（逆等线几何模型）

逆等线、最值问题 (近几年中考比较流行此类题目)

等腰△ABC中，E、F分别是腰AB、AC上的动点，且AE=CF，即逆向相等，则EF称为等腰△ABC的逆等线。一般情况下题目中有两个没有首尾相连的线段相等，也归为逆等线问题。

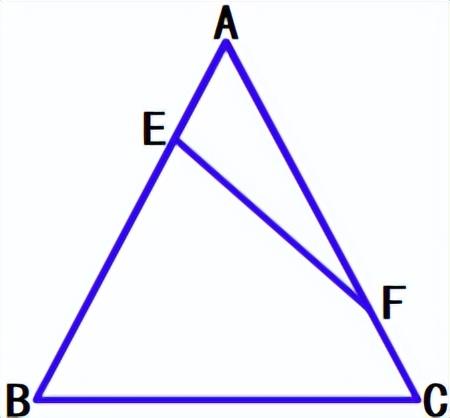
由于AE与CF没有首尾相连，所以一般通过平移、构造全等三角形等方法转移线段，使它们产生联系。

这个例题是最常见的逆等线求最值的问题

固定的△ABC中，D、E分别是AB、AC上的动点，且AD=CE，求BE CD的最小值。

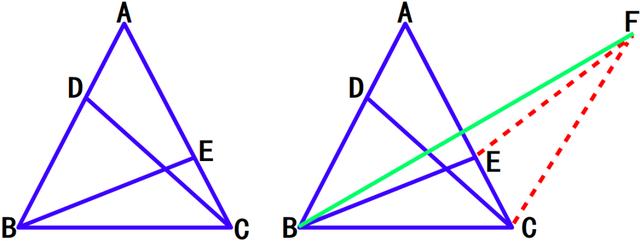
如图，通过构造全等三角形，△CEF≌△ADC，使D、E双动点转化成单动点，BE CD转化成BE EF，最小值就是定点B、F间的距离。具体题目中会给出一些特殊角度，便于计算BF的长度，最常见的是等边三角形，直角三角形。

下面是练习题，构造方法非常多，解析仅供参考。

①如图△ABC，AB=AC，∠BAC=90°，E、F分别在AB、AC上，且AE=CF，AD⊥EF交BC于D，求证EF=AD。

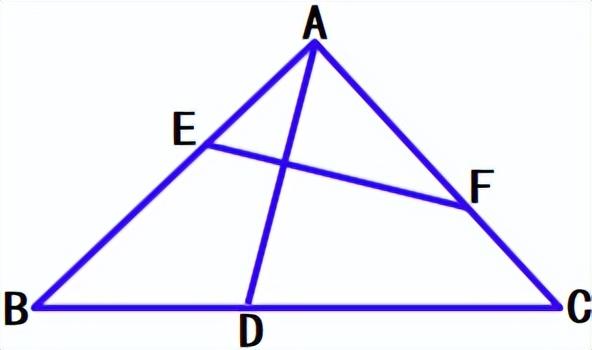
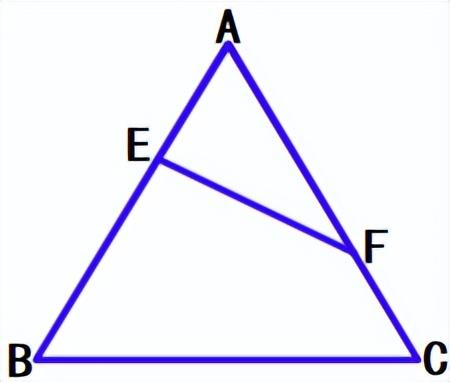
②等边△ABC的边长是6，E、F是AB、AC边上的动点，且AE=CF，求EF的最小值。

③如图△ABC，∠ABC=60°，点D、E分别在BC、AC上，且AE=CD，若AB=4，AC=5，求AD BE的最小值。

④如图△ABC，∠BAC=90°，点D、E是BC边上的动点，且BD=CE，若BC=5，求AD AE的最小值。

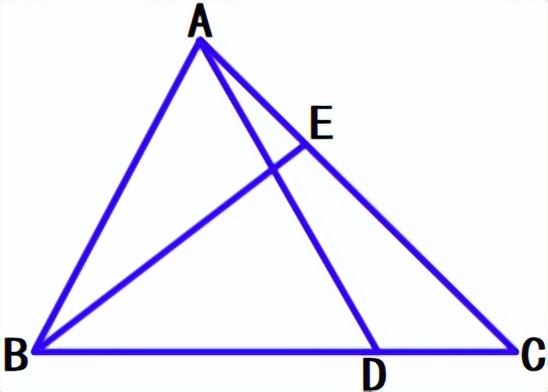
⑤如图，矩形ABCD，AB=3，AD=4，点E、F分别是线段AC、BC上的动点，且AE=CF，求DE DF的最小值。

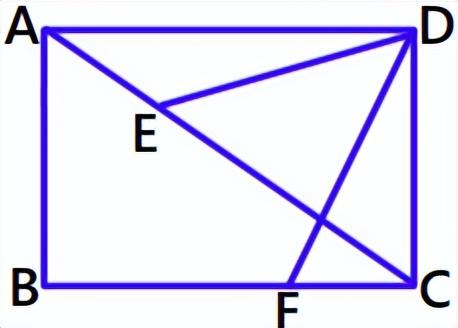
⑥如图，矩形ABCD，AB=2，AD=1，G是AB中点，E、F分别是AD、CD边上的动点，且CF=2AE，求GF 2BE的最小值。

需要PDF打印版可以找刘老师（shenyangmath）领取。

以下是练习题的答案与解析，解题方法多种多样，仅供大家参考。

①答案：简证如下

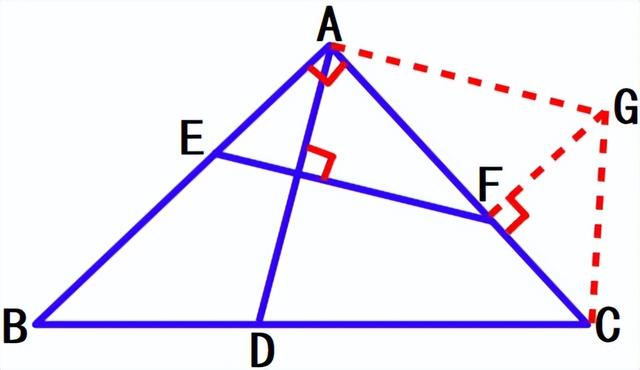
把EA平移到FG，连接CG、AG，则四边形AEFG是平行四边形，AG=EF。△FCG是等腰直角三角形，∠ACG=45°。

因为∠CAG=∠BAD，AB=AC，∠ACG=45°=∠B，所以△ACG≌△ABD(ASA)，AG=AD，所以EF=AD。

②答案：3

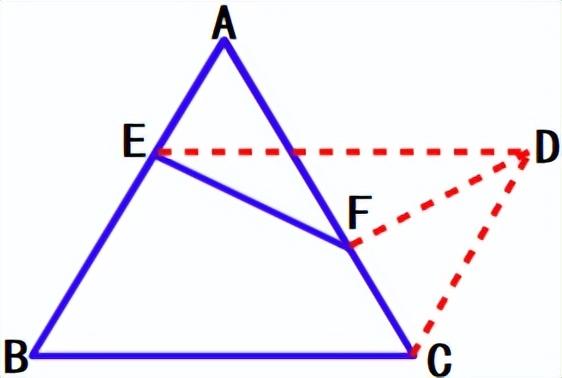
利用条件AE=CF，构造△CDF≌AFE。

如图，过C作CD∥AB，且CD=AF，则∠DCF=∠FAE，△CDF≌△AFE(SAS)，所以DF=EF。

易知四边形BCDE是平行四边形，所以DE=BC=6。

EF DF=2EF≥DE，当EFD三点共线时取等号(此时EF∥BC)。所以EF的最小值是3。

③答案：√61

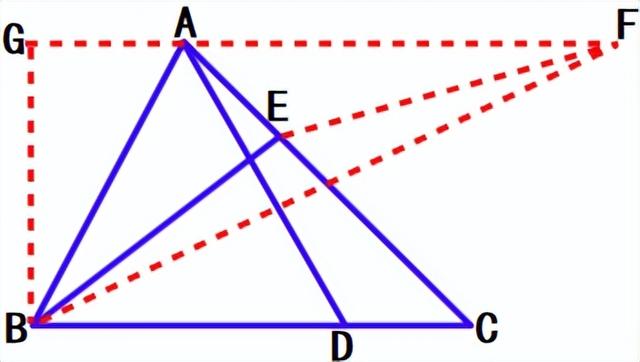
利用AE=CD，构造△AEF≌CDA，把AD转移到EF，则与BE相连。

过点A作AF∥BC，且AF=AD。则∠EAF=∠C，所以△AEF≌△CDA(SAS)，所以AF=AC=5。

转化成BE EF的最小值，且B、F都是定点，BE EF≥BF

接下来求出BF即可。延长FA，过B作BG⊥FA于点G，则∠ABG=30°，AG=2，GF=7，BG=2√3。

BF²=BG² GF²=12 49=61，所以BF=√61，即AD BE的最小值是√61。

④答案：5

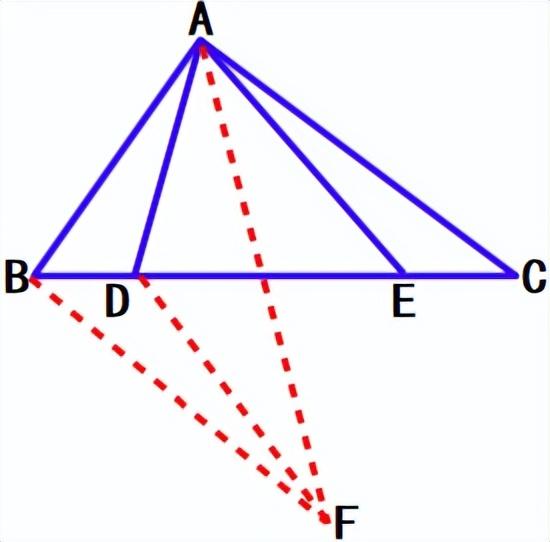
利用BD=CE，构造△BDF≌CEA，把AE转移到DF，则与AD相连。

过B作BF∥AC，BF=AC，则∠DBF∠C，所以△BDF≌△CEA(SAS)，所以BF=AC，DF=AE。

AD AE=AD DF≥AF。

接下来求出AF即可。易知△ABF≌△BAC(SAS)，所以AF=BC=5，即AD AE的最小值是5。

⑤答案：√985 / 5

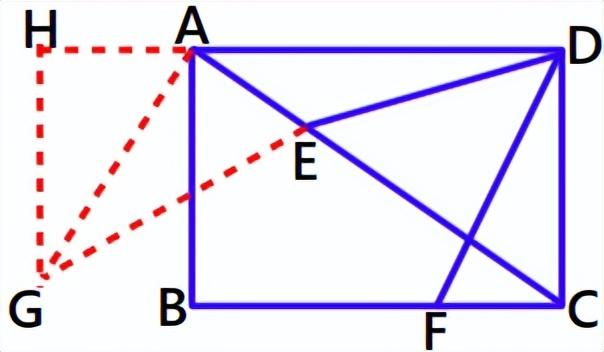
利用AE=CF，构造△AGE≌CDF，把DF转移到EG，则与DE相连。

过点A作AG⊥AC，且AG=CD。则△AGE≌△CDF(SAS)，所以AG=CD=3。

转化成DE EG的最小值，且G是定点，DE EG≥DG

接下来求出DG即可。延长DA，过G作GH⊥DA于点H，则△GAH∽△ACD(一线三垂直)，AC=5，容易求出AH=9/5，GH=12/5，所以DH=29/5，直角△DHG中根据勾股定理求出DG=√985 / 5。

⑥答案：√26

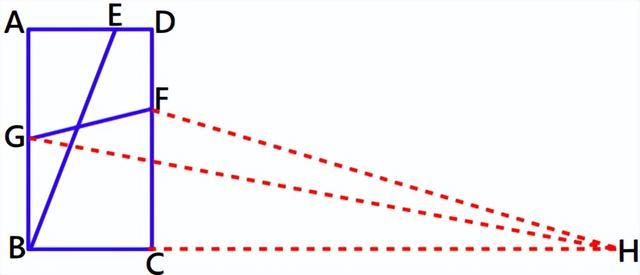
此题给的是线段的2倍关系，不能构造全等，但是可以构造相似。

利用CF=2AE，构造△CHF∽△ABE，把2BE转移到FH，则与GF相连。

延长BC至H，使CH=2AB，则△CHF∽△ABE，所以FH=2BE。

GF 2BE≥GH。

接下来求出GH即可。GB=1，BH=BC CH=1 4=5，根据勾股定理可得GH=√26。

♡♡♡感谢大家的支持♡♡♡

,