pac设计法（高效率PA设计从ClassA到Class）

在以上材料中，我们讨论到：PA设计中可以依靠“简单功率合成”来进行功率的合并，也可以利用“特殊功率合成”，达到高效率、负载不敏感等设计需求。材料推出去之后，一些朋友发来问题：提升效率只能依靠架构上的改变吗？一些PA没有用到Doherty等复杂的架构，依然取得了不错的效率，是怎么做的呢？

这些问题没有一个简单的答案可以回答。于是我们想，那就不如把PA在高效率设计中的考量讨论的再细节一些：不止是定性的讨论到宏观架构，而是深入到单个PA设计的思考取舍中。

在PA设计的细节考量中，最重要的一个概念就是PA的“类”别了，也即PA的Class。比如我们经常提到的Class A、Class AB、Class E及Class F等。不同Class的PA有不同的特点，我们这份材料就以PA的Class为线，讨论手机射频PA的“高效率（High Efficiency）”设计。

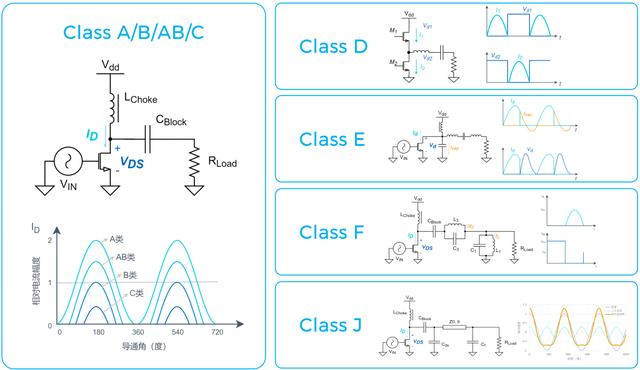
图：PA设计的“类”别分类

PA设计的重要指标

在讨论PA的类别之前，首先将PA设计中的重要指标做一个探讨。

PA是用来将直流能量转化射频信号的器件。PA通常工作在大信号状态，其工作状态与偏置点、负载阻抗、谐波控制、功率的过驱动等都有关系，设计和分析起来非常复杂。

尽管一款性能优异的PA设计复杂，但PA的评价指标却相对简单，最重要的两个指标就是：线性度，效率。

线性度

在现代PA设计中，线性度反应输出信号的失真程度，是一个重要指标。

在衡包络通信系统中，如FM，FSK，GMSK，信号包络并不承载信息，所以并不需要信号的线性放大，“线性度”并不是一个重要指标。但在现代通信系统中，为了最大化的利用频谱资源，出现了如高阶QAM等非等幅信号调制方法，也诞生出了CDMA及OFDM等多工方式，其幅度不再恒定不变，而是承载通信信号信息。下图为带有幅度调制信号的OFDM信号在时域的波形构成。

图：OFDM信号在时域的波形构成，幅度不再恒定

在这些信号中，为了表征信号幅度变化的大小，信号“功率峰均比”的概念被引入了进来。峰均比的英文是Peak to Average Power Ratio，简称PAPR，是指信号峰值功率与均值功率的比值。一般线性信号的PAPR在3~9dB之间。下图为某典型OFDM信号能量谱分布，可以看到信号幅度在0~11.55dB之间呈现概率分布。

图：典型信号的概率分布

由于这些高阶调制方式的信号中的幅度与相位均带有信息，这时必须要对信号进行线性放大，才能使幅度信息不失真的进行传递。若PA本身存在非线性，则PA对不同大小信号展现出不同的响应，就会产生非线性失真，使ACLR、EVM等指标产生恶化，影响系统的通信能力。

效率

PA的本质是把直流能量转化为大功率的射频信号，PA的效率反应了转换能力的大小。所以“效率”成为PA设计中另一个重要指标。

PA的效率由两种定义方式，分别为功率转换效率（Efficiency），和功率附加效率（Power Added Efficiency）。

功率转换效率的定义是输出功率与消耗直流之比，通常用η表示，计算公式为：

PAE的定义将输入功率也考虑进来，只计算经过PA后“增加的”功率部分与直流耗散之间的比值，所以被称作功率“附加”效率。PAE的计算公式为：

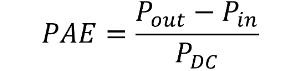
当PA增益足够大时，Pout将远大于Pin。比如当PA增益为30dB左右时，Pin只有的千分之一。这时PAE与功率转换效率的计算结果基本相同。

PA的效率和线性度之间是一对折中。在PA设计中，不断的对这两个指标进行优化或者取舍。

效率优化的理念

根据效率定义的公式可以看出，如果直流能量PDC被完全转化为了基波射频能量Pou，则PA将达到梦寐以求的100%的效率，能量一点也不被浪费。

但这个100%的效率是不可达成的，因为在实际电路中，一定会有一部分直流能量转换为谐波射频能量Pout,nf以及直流耗散能量Pdiss。三种能量与直流能量的关系如下公式所示：

高效率PA的设计理念就是：尽量使得以上公式的后两项：直流耗散能量、谐波耗散能量，趋近于零。

• 直流耗散能量（Pdiss）趋向于0

直流耗散能量的计算方法为流过晶体管的电压与电流的乘积对时间的积分，其公式可以表示为：

若使此能量等于零，则时域表现为二者之间在时域尽量少的交叠。以上设计观念在高效率PA中经常被采用，尤其是在F类、E类等开关类PA设计中。

• 谐波能量（Pout,nf）趋于0

PA是一个大功率工作器件，一般PA都会工作在带有一定非线性的工作状态，这时就会产生谐波能量。

对于n次谐波，其能量可以表示为：

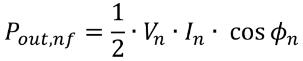
以上公式中，Vn与In分别为n次谐波的电压与电流摆幅幅值，Φn为其相位。

为了达到100%的效率，需要控制能量不被谐波能量所消耗。如果有谐波能量，即使直流消耗为0，也无法达到100%的效率。一个典型的例子是当PA的电压与电流均是完美方波的情况下，电压与电流无交叠，直流耗散Pdiss为0。但此时电压与电流均存在奇次谐波能量，奇次谐波能量不为0。通过傅里叶展开可计算，此时PA的最大效率只有：

即在电压电流均是完美方波的情况下，谐波部分抢走了近1/5的能量。下图为此时电压与电流的时域波形，以及能量在频域的分布。

图：电压与电流均为方波时，时域波形与频域能量分布

为了减少直流耗散能量、谐波耗散能量这两大损耗，在高效率PA中不断要考虑电压与电流波形之间的关系，对波形进行塑造，提升PA效率。这种工作在PA设计中被称为“波形工程（Waveform Engineering）”。

PA Class的分类

为了优化PA的线性度和效率，在射频PA先驱者过去100多年的工作中，根据工作类型的不同，将PA分为不同的类型（Class）进行分析和设计。

射频PA设计中所涉及的主要类别有：

• A类

• B类

• AB类

• C类

• D类

• E类

• F类

• J类

线性与开关类PA

以上类别中，可以根据工作方式的不同，分为线性PA类与开关PA类。

线性PA类是指利用晶体管线性区特性，实现功率放大的放大类型。在这个工作区域内，晶体管的输入和输出成大致线性的转移关系，输出信号幅度的大小可以反应输入信号幅度的大小。

需要注意的是，对于BJT与FET的工作原理不同, 二者 “线性区域”有不同的称呼方法。在BJT器件中，这个区域被称为线性放大区，或线性区；而在FET器件中，这个区域被称作饱和区。

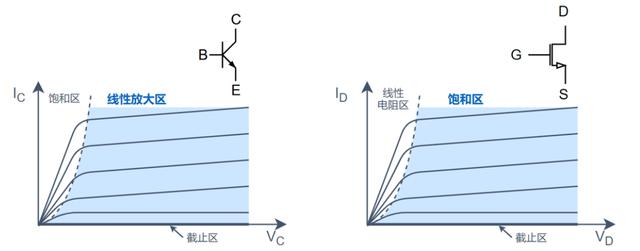
图：BJT与FET器件用于实现线性PA的工作区域

线性PA的主要类型有A类、B类、AB类和C类等。

需要说明的是，线性PA并不是完全没有非线性。对于除A类外的AB类、B类和C类线性放大器，因为波形的非完整周期导通，输出均存在非线性分量。即使对于全周期导通的A类放大器来说，由于晶体管输入和输出的非线性转移关系（指数或者二次方关系），输出也会出现非线性分量。但这些非线性分量的存在，不影响晶体管工作在线性工作区的实质，也不影响输出信号幅度与输入信号幅度呈正向比例的相对关系，所以这些PA都属于线性PA。

图：晶体管的转移特性

因为理解直观，设计容易，线性PA是放大器设计中的首要选择。但线性PA很难做到高效率，于是PA设计先驱者开始将开关类PA的设计理念引入进来。

开关类PA类型主要有D类、E类、F类和J类等，其特点是晶体管工作在类似开关状态。在这些PA设计中，对PA的设计考虑不再局限于从A/B/AB/C类放大器中偏置的角度讨论，而是把输出端负载对波形的调制影响也考虑进来。

“高效率”是开关类PA的传统优势，但其线性度较差。并且，进入到高频之后，由于寄生效应的存在，并不能实现完美的开关特性，谐波控制也变的困难，这些都给开关类PA的设计带来挑战。

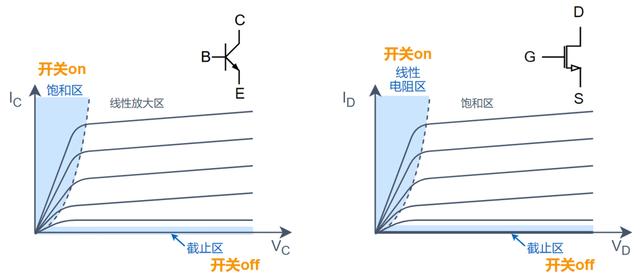
图：用于实现开关PA的工作区域

线性类PA

线性类PA简化电路如下图所示：

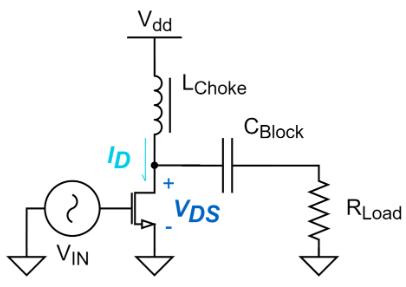
图：线性类PA简化电路示意图

根据晶体管导通角的不同，可以将线性PA分为A类、AB类、B类和C类。不同类型PA的偏置状态与导通角的关系如下图所示：

图：各类线性放大器偏置状态与导通角的关系

A类PA

A类PA的晶体管在信号的全周期导通。其电压与电流的波形如下图所示：

图：A类PA的电压与电流波形

假设A类PA的直流工作点为VDC与IDC，射频信号摆幅为VRF与IRF，则根据PA效率的定义，A类PA的效率可表示为：

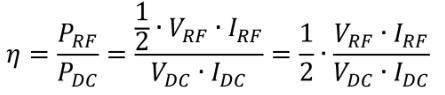
A类PA最大效率在VRF与IRF达到最大摆幅VDC与IDC时取得，为50%。

在输出功率变小时，A类PA射频功率变小，但DC功耗不变，使得其效率明显下降。在输出功率下降至最大A类输出功率的一半时，其效率也将下降一半。即在功率回退时，其效率以2倍/3dB（10倍/10dB）的速度下降。

图：A类PA功率回退时的效率特性

B类PA

B类PA的直流偏置点放置在晶体管导通开启电压附近，只有当输入信号为正向摆幅时晶体管导通，导通角只有全周期的一半。B类PA的电压与电流波形如下：

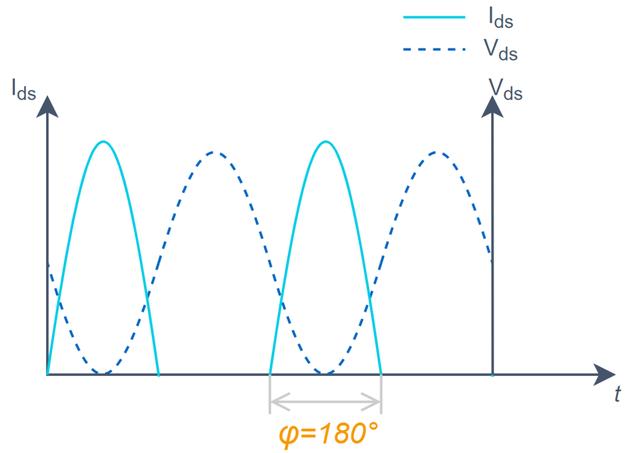
图：B类PA的电压与电流波形

虽然输出电流只有半周期导通，波形出现了强烈的失真，但由于器件仍然工作于线性工作区域，输入信号的幅度仍然基本正比于输入信号的幅度，所以B类PA仍然是线性类PA。

分别对基波和DC进行积分，可以推导得出导通角为2θ（2θ=φ）的PA最大效率表达式为：

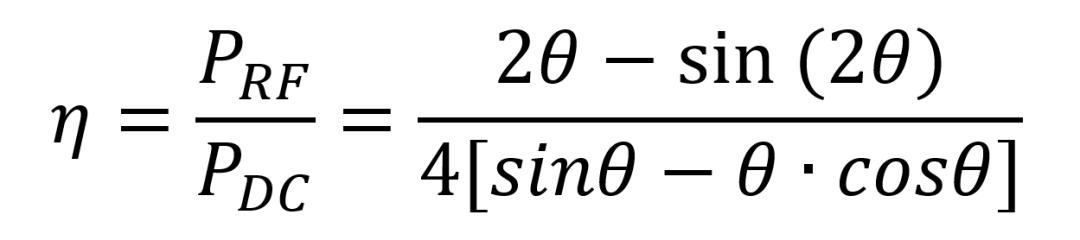
对于B类PA，2θ=π，则上式推导为：

所以相比于A类放大器50%的最高效率，B类放大器的最高效率可提高至78.5%。

AB类PA

AB类PA是指处于A类和B类之间的PA类型，导通角为在π与2π之间，其电压与电流波形如下：

图：AB类PA的电压与电流波形

AB类PA的效率根据导通角的不同而不同，处于A类的50%与B类的78.5%之间。

C类PA

通过带有导通角的效率计算公式可以看到，当导通角变小时，PA的效率提升。在B类PA的基础上继续减小导通角，全周期的导通角减少至180度以下时，就形成了C类PA。C类PA的电压与电流波形如下图所示。

图：C类PA的电压与电流波形

对于C类PA，将导通角取0为极限，可以得到PA的极限效率可达100%。

虽然理论上C类PA可以达到100%的效率，但达到100%效率时导通角为0，此时也无功率输出。所以C类PA中的100%效率是可望而不可及，无法为实际使用的PA设计提供有效帮助。

线性类PA比较

由于导通角的不同，A类、AB类、B类及C类PA在效率、基频功率，以及谐波功率上有不同的表现。采用傅里叶变换可以对几种不同类型的PA进行分析，得到几种类型的PA特性如下图所示[8]：

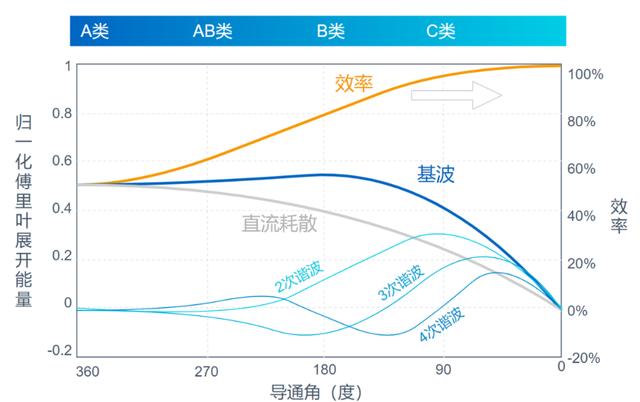
图：不同导通角下PA的能量分布及效率特性

依靠上图，可以很好的理解不同类型的线性PA的特性关系，可以看到：

1. 随着导通角变小，PA效率由50%逐渐提高至100%

2. 从A类到B类的变化中，导通角的变小并没有引起基波能量的减小

3. 从B类到C类变化中，基波输出功率迅速减小

   
   

正是由于以上特性，应用中线性PA大多设计在AB类，这时有较好的效率，较高的基波输出功率，同时也有可接受的谐波特性。

开关类PA

在理想开关类PA中，当输入电压为正，晶体管打开，电流通过晶体管，此时晶体管两端电压为0；当电压为负，晶体管关闭，此时输出电压开始建立，但流过晶体管的电流为0。

因为作为开关使用的晶体管不消耗功耗，所有的能量都可以转化为射频能量，所以理论上开关PA可以达到100%的效率。

然而在实际使用中，由于开关的非理想特性和器件的寄生效应，晶体管并不能达到理想开关状态，也就造成了电压与电流的部分交叠，造成效率的损失。另外，如果谐波能量处理不当，也会引起能量损失。

为了使开关类PA的效率不断逼近100%，PA设计先驱们采用了多种不同的设计分析方法，于是就产生出多种不同的开关PA类型。在射频PA中，最主要的有D类、E类、F类以及J类PA。

D类PA

D类PA是1959年由Baxandall教授首先提出[2]，其构成为一个成对的开关管M1及M2，以及谐振在基波频率的调谐负载。

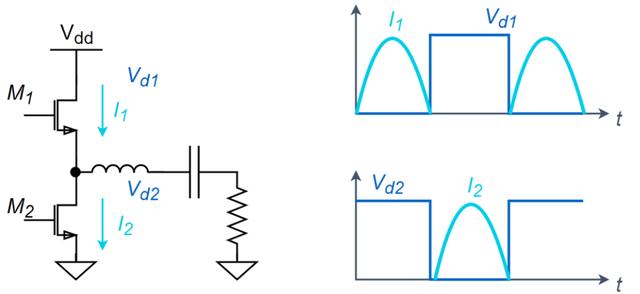
图：D类PA工作原理及波形

理想情况下，D类PA晶体管的电压与电流无交叠，使得D类PA直流功率耗散为0。

对于谐波功率耗散，D类PA的输出电压波形为方波信号；由于谐振负载的存在，输出电流波形为半正弦波。对方波信号进行傅里叶展开，所有的偶次谐波分量为0；对半正弦波进行傅里叶展开，所有奇次谐波分量为0。谐波分量中电压与电流交替为0，使得理想D类PA的无谐波功率耗散。

以上这种电压与电流分别为方波与半正弦波时，在谐波功率耗散为0的特性，在高效率PA设计中经常被使用。

由于直流功率耗散与谐波功率耗散均为0，所以理想D类放大器可以达到100%的效率。

D类PA也有一系列变形，例如可以将电流构建成方波，将电压构建成半正弦波。这种就是电流模式的D类放大器。其简化电路及波形图如下图所示。

图：电流模式的D类放大器

E类PA

D类PA看起来可以完美实现100%的转换效率，但其高度依赖两个开关管的完美切换，在高频应用时显得无能为力：感性的负载会使开关“关不断”，容性负载会使开关“打不开”。并且D类PA需要的成对推挽结构，也使得其在部分高频应用时力不从心。

为了使开关类PA可以应用在高频频率，Sokal教授在1975年发明了E类PA[3]。E类PA由工作于开关状态的单端晶体管、负载匹配网络构成。其架构如下图所示。

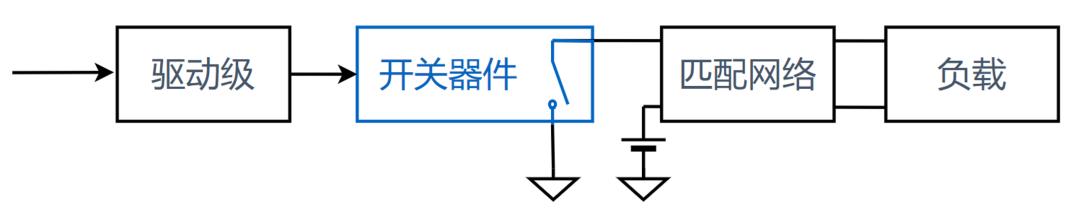
图：E类放大器框图

E类PA的架构看起来与普通的A类、AB类PA并无大的不同，但设计思路却相差很大。E类PA的设计理念是：

• 首先将晶体管的偏置和驱动功率进行合理设计

• 然后对输出波形提出一系列约束条件，这些约束条件使晶体管工作于开关状态

• 基于这些约束条件，就可以计算不同拓扑中器件取值，从而完成设计
  
  

E类PA约束条件使作为开关等效的晶体管在合适的时间进行off到on的切换，从而减小开关切换过程中带来的充放电损耗。Sokal教授提出E类PA设计的两个重要约束条件：

1. 当开关从off到on转换的瞬间，漏极电压为零（Zero voltage switching，简称为ZVS）

2. 当开关从off到on转换的瞬间，漏端电压波形的斜率为零（Zero voltage derivative switching，简称ZVDS）
   
   

E类放大器的简化等效电路与波形示意如下图所示。

图：E类放大器的简化电路，以及波形示意图

F类PA

F类PA的发明源自对过激励的B类PA的研究。

在线性PA分析中，B类放大器的最大效率为78.5%，但如果对其进行过激励驱动，其电压、电流波形出现削峰，形成类似方波的波形，这时电压电流交叠变少，从而效率得到提高。

图：理想过激励下B类放大器的电流与电压波形

过驱动的B类放大器虽然有更高的效率，但由于电压电流均都包含奇次和偶次谐波，有部分能量仍然消耗在了谐波上，所以效率无法达到100%。通过计算，过驱动的B类放大器可以达到88.6%的效率。这就是为何有些B类放大器能看到高于理论值78.5%的峰值效率的原因。

基于对过驱动的B类PA的研究，D. M. Snider教授于1967年提出F类PA的概念[4]，随后F. H. Raab等教授将F类PA的原理和设计方法进行了更进一步阐述[5][6][7]。

F类PA通过对谐波阻抗的控制，使奇次谐波阻抗为开路，偶次谐波阻抗短路，于是得到方形的电压波形，和半正弦的电流波形。由于二者分别只含有奇次和偶次谐波，谐波消耗为0，在理想情况下可得到100%的效率。下图为理想F类PA的电压电流波形。

图：理想F类PA的电流及电压波形

在实际应用中，由于谐波频率高，无法对各次谐波阻抗均进行完美控制，这在一定程度上恶化了F类PA的实际应用效果。下图为对3次谐波进行控制的F类PA简化电路[5]。

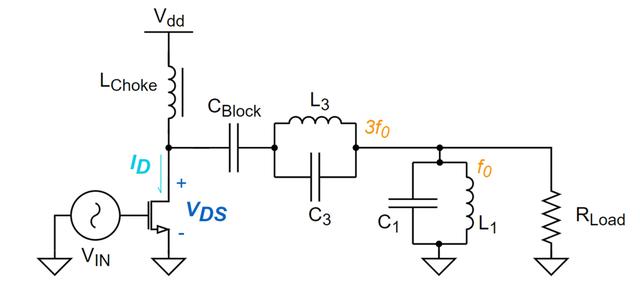
图：典型的F类PA电路

同理，也可以将电流构造成方波，电压构造成半正弦波，同样可以达到理论上100%的效率，这样就形成了逆F类PA的设计。逆F类PA设计的条件与F类放大器相反：偶次谐波阻抗需要设计成开路，奇次谐波阻抗需要设计成短路。

图：理想逆F类PA漏极电流及电压波形

虽然F类和逆F类在理论上都可以达到100%的峰值效率，但在实际应用中，二者表现还是会稍有不同。考虑晶体管Knee电压之后，F类和逆F类PA的工作区域如下图所示，从图示对比可以推导出系列F类与逆F类PA之间性能比较的关系。以上推导在本文中不再赘述。

图：F类与逆F类PA电压及电流摆幅关系比较

J类PA

J类PA是Cripps教授于2006年提出的一种高效PA设计方法，其设计思路仍然是利用谐波阻抗的控制，实现电压与电流交叠部分的减少，从而减少直流损耗，提升PA效率。下图为Cripps教授提出的J类PA的简化电路图 [8]。

图：J类PA简化电路

与F类通过控制不同次谐波的幅度来构建完美的方波与半正弦波不同，Cripps教授的想法是通过控制二次谐波的相位，使二次谐波与基波之间形成叠加，减小电压与电流之间的交叠。

图：J类PA电压波形示意图

对J类放大器进行效率计算，可以得到J类放大器的最大效率为78.5%。

虽然J类PA与B类PA的效率相同，但理想B类PA需要二次及以上谐波均短路，这在物理上不易实现。而J类PA要求二次谐波处于某一个虚部值即可，这在实际工程中实现更容易，并且有较好的宽带特性。

不同类型PA的比较

相对功率输出力

在PA设计中，评价不同结构的特点时，除了效率、功率指标，还有一个重要指标，称为“归一化功率输出能力”，英文为Normalized Output Power Capability，一般简写为PNOPC。其定义为：功率放大器的最大输出功率和最大瞬态工作电流与电压乘积之比。公式可以表示为：

归一化功率能力指标可以反应在给定的电压与电流摆幅的情况下，功率放大器输出最大功率的大小；也可以反应在给定输出功率的情况下，所需要电压与电流摆幅的大小。

对于A类放大器，其归一化功率输出能力可计算为：

同理，可计算出其他类型PA的相对功率输出能力。

不同类型PA性能对比

将以上讨论到的PA特性进行总结，得到性能对比如下图所示。

图：不同类型PA特性对比

总结

在很多人看来，PA设计像是“黑魔法”，难以捉摸。

说PA设计是“黑魔法”，是因为在很多时候，PA的状态看起来是不受控的。甚至有时PA的性能已经出来了，Designer都说不清它是怎么工作的。

PA虽然看起来这么的不可控，但它并不是“魔法”，它也是严格遵循物理规律的。在过去100多年发展中，PA设计的先驱和专家们不断想办法对它进行理解。“不同的Class”分类，是先驱专家们总结出理解PA特性的经典方法，在高效率PA设计中得到有效使用。

本文对常见射频PA的类别进行简单总结，希望对大家在高效率PA的设计和应用中有所帮助。

本文整理过程中得到众多行业专家的帮助，在此表示诚挚感谢！

---

参考文献

[1]. Anoh K, Adebisi B, Rabie K, et al. On Companding and Optimization of OFDM Signals for Mitigating Impulsive Noise in Power-Line Communication Systems[J]. IEEE Access, 2017.

[2].Baxandall P J. Transistor sine-wave LC oscillators. Some general considerations and new developments[J]. Proceedings of the IEE - Part B: Electronic and Communication Engineering, 1959,106:748-758.

[3].N. O S, A. D S. Class E-A new class of high-efficiency tuned single-ended switching power amplifiers[J]. IEEE Journal of Solid-State Circuits, 1975,10(3):168-176.

[4].Snider D M. A theoretical analysis and experimental confirmation of the optimally loaded and overdriven RF power amplifier[J]. IEEE Transactions on Electron Devices, 1967,14(12):851-857.

[5].Raab F H. Class-F power amplifiers with maximally flat waveforms[J]. IEEE Transactions on Microwave Theory and Techniques, 1997,45(11):2007-2012.

[6].Raab F H. Maximum efficiency and output of class-F power amplifiers[J]. IEEE Transactions on Microwave Theory and Techniques, 2001,49(6):1162-1166.

[7].Raab F H. Class-E, Class-C, and Class-F power amplifiers based upon a finite number of harmonics[J]. IEEE Transactions on Microwave Theory and Techniques, 2001,49(8):1462-1468.

[8].Cripps S C. Rf power amplifier for wireless communications [M]. RF power amplifiers for wireless communications /, 2014.

,