算法分析经典题型（读题技巧列表方法）

叶先玖（湖北省秭归县归州中学）

何训光（湖北省秭归县教育科研信息中心）

摘要：让每一位学生学会解答应用题，掌握解答应用题的技巧和策略，是每一位教师都渴望的.教师都知道列表分析法是一种重要方法，但在实际教学中却不能真正把这种方法用到极致。文章在读题的方法和步骤，列表的分步操作方法和技巧，以及如何建立方程模型这三个方面做了较为全面的探究，是一种帮助广大教师和学生掌握解决复杂应用问题的最佳方法.

关键词：读题技巧；列表方法；建模思想

探索具体问题中的数量关系和变化规律，掌握用代数式、方程、不等式、函数进行表述的方法，这是《义务教育数学课程标准（2011年版）》对初中阶段知识与技能板块提出的一个重要目标。在现实生活中蕴含着大量与数量有关的问题，这些实际问题需要转化成数学问题来解决，即人们常说的数学应用题.然而，现在的学生多数却害怕解应用题，就连部分教师见到相对复杂一点的应用题也是望而生畏.说轻一点，这是导致学生认为学习数学没有作用的一个重要方面，因为学生根本就不会用数学的方法解决生活问题；说得严重一点，这是导致我国学生普遍缺失应用意识和创新能力的关键.

其实，解决任何事都是会有一种好的办法的，也许是因为你暂时没有找到，或者是因为你根本就认为没有好方法，因而没有去认真研究和寻找.解答应用题就和解决其他任何问题一样，都会有好方法的，而且也许不只有一种、两种.例如，“读题—列表—建模”就能解决很多复杂的应用问题，下面笔者就以此种方法为例加以说明，希望能给读者在今后的教学或学习、生活和工作中起到帮助作用.

例1 （2014年湖北·宜昌卷）在“文化宜昌•全民阅读”活动中，某中学社团“精一读书社”对全校学生的人数及纸质图书阅读量（单位：本）进行了调查，2012年全校有1000名学生，2013年全校学生人数比2012年增加10%，2014年全校学生人数比2013年增加100人．

（1）求2014

年全校学生人数；

（2）2013年全校学生人均阅读量比2012年多1本，阅读总量比2012年增加1700本（注：阅读总量=人均阅读量×人数）.

①求2012年全校学生人均阅读量；

②2012年读书社人均阅读量是全校学生人均阅读量的2.5倍，如果2013年，2014年这两年读书社人均阅读量都

比前一年增长一个相同的百分数a，2014年全校学生人均阅读量比2012年增加的百分数也是a，那么2014年读书社全部80名成员的阅读总量将达到全校学生阅读总量的25%，求a的值.

1、初读找准数

具体方法：只读数，并快速地在题中把数字或字母标上同一种记号.

如，此题中可以要求学生解答下列问题：题中涉及有价值的数字依次有哪些？在题目中读出，并做上记号.学生很快能找出1000，10%，100，1，1700，2.5，a，a，80，25%.这里要注意纠正学生把2012，2013，2014这些对象认为是此题的“数”的错误认识.

2、再读确定量

具体方法：即在标有记号的数字部分反复阅读，读出每个数的实际意义，即读懂每个数字或字母所表示的含义.

如，师生共同研读出“10%”对应量是2013年全校学生人数比2012年增加的百分数、研究对象是2013年； 第一个“a”对应量是书社人均阅读量增长的百分数，研究对象是2013年，2014年；第二个“a”对应量是全校人均阅读量，研究对象是2014年等；引导学生在题目中用另一种相同记号把各个数对应的量做上记号.

3、细读建表格

具体方法：这一次阅读主要是仔细读做上记号的数及量，关键是读懂每个数表示的意义。边读边在草稿纸上制作表格.此题具体过程如下.

4、研读理关系

具体方法：这一步主要是填写表中空白单元格.方法是某一个空白单元格和其他单元格涉及关系较多时，也就是箭头符号所在单元格较多的空白单元格（表5中的第3行第2列），先大胆设成未知数。再仔细研读表格中各个数、量、对象之间横向、纵向的对应关系，把表格各单元格转化成代数式，快速实现“数学化”，如表6所示.再横向、纵向查看还有哪些箭头符号在这一过程中没用上，这个没用上的或许就是我们要用来列方程的等量关系.

表6

5、读表建模型

具体方法：分析表6的第2行轻松地完成第（1）问；由第4行第2，3列，建立一元一次方程，自然求得2012年全校学生人均阅读量为6本；按照表中第4列，第4行，第7行，我们就能很快地建立起一元二次方程模型了.

解：（1）由题意，得2013年全校学生人数为1000×（1 10%）=1100（人）.

则2014年全校学生人数为1100 100=1200（人）.

答：2014年全校学生人数为1200人.

（2）①设2012人均阅读量为x本，则2013年的人均阅读量为（x 1）本.

由题意，得1100（x 1）=1000x 1700.

解得：x=6．

答：2012年全校学生人均阅读量为6本.

②由题意，得2012年读书社的人均读书量为2.5×6=15本。

2014年读书社人均读书量为15（1 a）

本，2014年全校学生的读书量为6（1 a）本，则80×15（1 a）

=1200×6（1 a）×25%.

解得a

=﹣1（舍去），a

=0.5．

答：a的值为0.5．

6、读解再反思

综观解答应用题的各种方法，本质上都是在学生读懂题目的基础上寻找数量关系，再合理利用等量关系进行数学建模.阅读理解能力较强的学生也可以不列表，同样能准确找出以下三个等量关系：2012年校人均阅读量 1=2013年校人均阅读量，2012年校阅读总量 1700=2013年校阅读总量及2014年读书社阅读总量=2014年校阅读总量×25%.再通过设出上述解答中的元，利用这三个等量关系转化为方程模型1100（x 1）=1000x 1700 ，80×15（1 a）

=1200×6（1 a）×25% 也可求解.但这种方法对各个量的关系显示得不直观，学生容易出错.而用“读题—列表—建模”法进行应用题解题时，却充分利用表格的直观性，学生在审题时会“去枝叶，抓主干”，准确抓住关键语句，并用小箭头清楚地显示各个量之间关系；在分析数量关系时，只要根据箭头所示，大胆设元（含间接设元），用两种方式计算同一个量，从而得到基本的方程模型，而且不同学生对单元格处理方式的角度不同，所得方程模型也不一样，从而实现一题多解.例如，在表5中换一个单元格设未知数，或者用不同代数式去表示相互有关系的两个单元格，对小箭头指示的关系处理角度不同等，可得到不同表达形式的表格6，从而得到此题的另一种解法，达到表格灵活性与解法多样性的完美结合.

例2 （2012年湖北·宜昌卷）背景资料：低碳生活的理念已逐步被人们接受．据相关资料统计：

一个人平均一年节约的用电，相当于减排二氧化碳约18kg；

一个人平均一年少买的衣服，相当于减排二氧化碳约6kg．

问题解决：甲、乙两校分别对本校师生提出“节约用电”“少买衣服”的倡议．2009年两校响应本校倡议的人数共60人，因此而减排二氧化碳总量为600kg．

（1）2009年两校响应本校倡议的人数分别是多少？

（2）2009年到2011年，甲校响应本校倡议的人数每年增加相同的数量；乙校响应本校倡议的人数每年按相同的百分率增长．2010年乙校响应本校倡议的人数是甲校响应本校倡议人数的2倍；2011年两校响应本校倡议的总人数比2010年两校响应本校倡议的总人数多100人．求2011年两校响应本校倡议减排二氧化碳的总量.

请读者在不看下面的分析的基础上先按上面的“读题—列表—建模”方法尝试着把此题解答出来.

因篇幅有限，笔者以下不再重复上面的“读题—列表—建模”的详细过程，仅帮助读者分析解题方法.

分析：此题考查了一元二次方程的应用及二元一次方程组的应用，解题的关键是找到正确的等量关系.

解：（1）（方法1）设 2009 年甲校响应本校倡议的人数为 x 人，乙校响应本校倡议的人数为 y 人，

解得n=1，n=－2.5（舍去）.

从而得m=20.

所以2011年两校响应该校倡议减排二氧化碳的总量为2040千克.

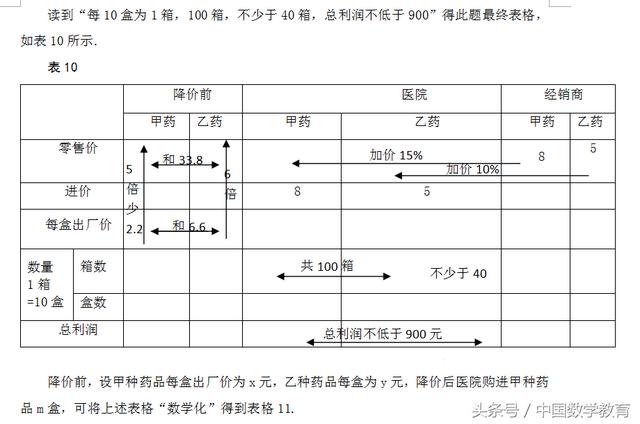
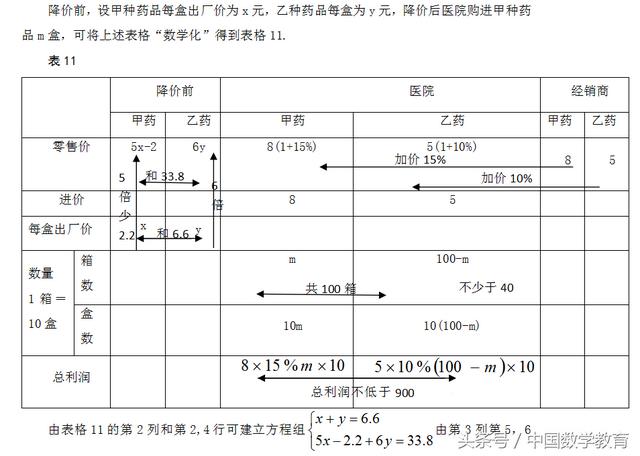
例3 （2014年江苏·盐城卷）整顿药品市场、降低药品价格是国家的惠民政策之一．根据国家《药品政府定价办法》，某省有关部门规定：市场流通药品的零售价格不得超过进价的15%．根据相关信息解决下列问题.

（1）降价前，甲、乙两种药品每盒的出厂价格之和为6.6元．经过若干中间环节，甲种药品每盒的零售价格比出厂价格的5倍少2.2元，乙种药品每盒的零售价格是出厂价格的6倍，两种药品每盒的零售价格之和为33.8元．那么降价前甲、乙两种药品每盒的零售价格分别是多少？

（2）降价后，某药品经销商将上述的甲、乙两种药品分别以每盒8元和5元的价格销售给医院，医院根据实际情况决定：对甲种药品每盒加价15%、对乙种药品每盒加价10%后零售给患者.实际进药时，这两种药品均以每10盒为1箱进行包装．近期该医院准备从经销商处购进甲、乙两种药品共100箱，其中乙种药品不少于40箱，销售这批药品的总利润不低于900元．试问购进时有哪几种搭配方案？

此题给出的信息量大，涉及厂家、医院、经销商、患者等多个对象，数量多、关系复杂，最适合用表格来分析。读“6.6”“ 5倍少2.2”“ 6”“ 33.8”得表8.

表8

“读题—列表—建模”法本质上是在数学模型思想指导下，读题时读懂数的含义，分析时借助表格揭示数量、对象之间的关系，建模时利用这些关系和代数式快速达到文字信息向符号信息转化，实现将实际问题数学化的目的.这种方法颠覆了学生传统的阅读方式和习惯，强调读题时先重点读数，后读数对应的是什么量，再读研究对象.由数找量再找对象，边读边把数、量、对象放在同一表格内，利用所得表格分析它们之间的关系并快速“数学化”，得到代数式、方程（组）、不等式（组）等数学模型.

从以上四例可以看出”读题—列表—建模”法的重点是读懂数，关键是列表，核心是找等量关系，技巧是利用表格进行推理来建立方程模型.当信息量大，一张表能清楚地反映出各种对象、数、量之间的复杂关系，给人一种思路清晰的感觉.但如何快速、熟练地建表，是需要从七年级就开始练习的，对学生长期有意识渗透这种读题习惯，培养他们边读数边列表来求解应用题的能力.否则，学生即使有这种想法，但往往苦于列不出一张表，反而对这种方法望而生畏.文章基本上能反映出我们在实际教学中的真实的做法，供大家参考，有不足之处，真诚希望得到同行的斧正.

参考文献：

[1]中华人民共和国教育部制定. 义务教育数学课程标准(2011年版)[M]. 北京：北京师范大学出版社，2012.

[2]仇锦华.小学与初中的应用题教学有何不同[J].中小学数学（初中版），2013(4)：1-2.

[3]李树臣.培养学生数学阅读能力的一般方法[J].中国数学教育（初中版），2011(4)：7-10.

[4]印冬建.应用题教学应突出建模过程的指导[J].中学数学教学参考：中旬，2013(8):35-37.

,