numpy五大函数（常用函数的内在机制）

支持大量多维数组和矩阵运算的 NumPy 软件库是许多机器学习开发者和研究者的必备工具，本文将通过直观易懂的图示解析常用的 NumPy 功能和函数，帮助你理解 NumPy 操作数组的内在机制。

矩阵操作

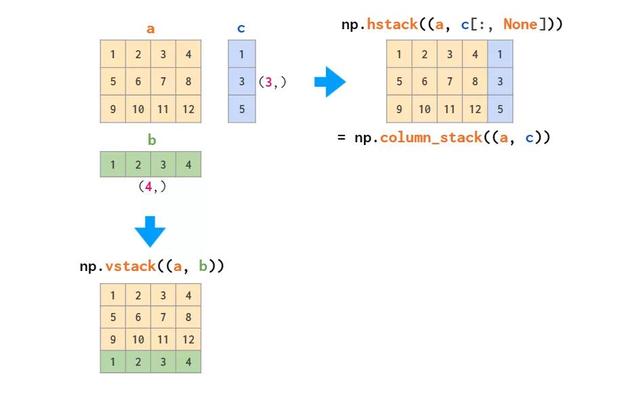
合并数组的函数主要有两个：

这两个函数适用于只堆叠矩阵或只堆叠向量，但当需要堆叠一维数组和矩阵时，只有 vstack 可以奏效：hstack 会出现维度不匹配的错误，原因如前所述，一维数组会被视为行向量，而不是列向量。针对这个问题，解决方法要么是将其转换为行向量，要么是使用能自动完成这一操作的 column_stack 函数：

堆叠的逆操作是拆分：

复制矩阵的方法有两种：复制 - 粘贴式的 tile 和分页打印式的 repeat：

delete 可以删除特定的行和列：

删除的逆操作为插入，即 insert：

append 函数就像 hstack 一样，不能自动对一维数组执行转置，因此同样地，要么需要改变该向量的形状，要么就需要增加一个维度，或者使用 column_stack：

事实上，如果你只需要向数组的边缘添加常量值，那么（稍微复杂的）pad 函数应该就足够了：

网格

广播规则使得我们能更简单地操作网格。假设你有如下矩阵（但非常大）：

使用 C 和使用 Python 创建矩阵的对比

这两种方法较慢，因为它们会使用 Python 循环。为了解决这样的问题，MATLAB 的方式是创建一个网格：

使用 MATLAB 创建网格的示意图

使用如上提供的参数 I 和 J，meshgrid 函数接受任意的索引集合作为输入，mgrid 只是切分，indices 只能生成完整的索引范围，fromfunction 只会调用所提供的函数一次。

但实际上，NumPy 中还有一种更好的方法。我们没必要将内存耗在整个 I 和 J 矩阵上。存储形状合适的向量就足够了，广播规则可以完成其余工作。

使用 NumPy 创建网格的示意图

没有 indexing=’ij’ 参数，meshgrid 会改变这些参数的顺序：J, I= np.meshgrid(j, i)——这是一种 xy 模式，对可视化 3D 图表很有用。

除了在二维或三维网格上初始化函数，网格也可用于索引数组：

使用 meshgrid 索引数组，也适用于稀疏网格。

获取矩阵统计数据

和 sum 一样，min、max、argmin、argmax、mean、std、var 等所有其它统计函数都支持 axis 参数并能据此完成统计计算：

三个统计函数示例，为了避免与 Python 的 min 冲突，NumPy 中对应的函数名为 np.amin。

用于二维及更高维的 argmin 和 argmax 函数会返回最小和最大值的第一个实例，在返回展开的索引上有点麻烦。为了将其转换成两个坐标，需要使用 unravel_index 函数：

使用 unravel_index 函数的示例

all 和 any 函数也支持 axis 参数：

使用 all 和 any 函数的示例

矩阵排序

axis 参数虽然对上面列出的函数很有用，但对排序毫无用处：

使用 Python 列表和 NumPy 数组执行排序的比较

这通常不是你在排序矩阵或电子表格时希望看到的结果：axis 根本不能替代 key 参数。但幸运的是，NumPy 提供了一些支持按列排序的辅助函数——或有需要的话可按多列排序：

1. a[a[:,0].argsort()] 可按第一列对数组排序：

这里 argsort 会返回原数组排序后的索引的数组。

这个技巧可以重复，但必须谨慎，别让下一次排序扰乱上一次排序的结果：

a = a[a[:,2].argsort()]

a = a[a[:,1].argsort(kind='stable')]

a = a[a[:,0].argsort(kind='stable')]

2. lexsort 函数能使用上述方式根据所有列进行排序，但它总是按行执行，而且所要排序的行的顺序是反向的（即自下而上），因此使用它时会有些不自然，比如

- a[np.lexsort(np.flipud(a[2,5].T))] 会首先根据第 2 列排序，然后（当第 2 列的值相等时）再根据第 5 列排序。

– a[np.lexsort(np.flipud(a.T))] 会从左向右根据所有列排序。

这里，flipud 会沿上下方向翻转该矩阵（准确地说是 axis=0 方向，与 a[::-1,...] 一样，其中三个点表示「所有其它维度」，因此翻转这个一维数组的是突然的 flipud，而不是 fliplr。

3. sort 还有一个 order 参数，但如果一开始是普通的（非结构化）数组，它执行起来既不快，也不容易使用。

4. 在 pandas 中执行它可能是更好的选择，因为在 pandas 中，该特定运算的可读性要高得多，也不那么容易出错：

– pd.DataFrame(a).sort_values(by=[2,5]).to_numpy() 会先根据第 2 列排序，然后根据第 5 列排序。

– pd.DataFrame(a).sort_values().to_numpy() 会从左向右根据所有列排序。

三维及更高维

当你通过调整一维向量的形状或转换嵌套的 Python 列表来创建 3D 数组时，索引的含义是 (z,y,x)。第一个索引是平面的数量，然后是在该平面上的坐标：

展示 (z,y,x) 顺序的示意图

这个索引顺序很方便，举个例子，它可用于保存一些灰度图像：a[i] 是索引第 i 张图像的快捷方式。

但这个索引顺序不是通用的。当操作 RGB 图像时，通常会使用 (y,x,z) 顺序：首先是两个像素坐标，最后一个是颜色坐标（Matplotlib 中是 RGB，OpenCV 中是 BGR）：

展示 (y,x,z) 顺序的示意图

这样，我们就能很方便地索引特定的像素：a[i,j] 能提供 (i,j) 位置的 RGB 元组。

因此，创建几何形状的实际命令取决于你所在领域的惯例：

创建一般的三维数组和 RGB 图像

很显然，hstack、vstack、dstack 这些函数不支持这些惯例。它们硬编码了 (y,x,z) 的索引顺序，即 RGB 图像的顺序：

NumPy 使用 (y,x,z) 顺序的示意图，堆叠 RGB 图像（这里仅有两种颜色）

如果你的数据布局不同，使用 concatenate 命令来堆叠图像会更方便一些，向一个 axis 参数输入明确的索引数值：

堆叠一般三维数组

如果你不习惯思考 axis 数，你可以将该数组转换成 hstack 等函数中硬编码的形式：

将数组转换为 hstack 中硬编码的形式的示意图

这种转换的成本很低：不会执行实际的复制，只是执行过程中混合索引的顺序。

另一种可以混合索引顺序的运算是数组转置。了解它可能会让你更加熟悉三维数组。根据你决定使用的 axis 顺序的不同，转置数组所有平面的实际命令会有所不同：对于一般数组，它会交换索引 1 和 2，对 RGB 图像而言是 0 和 1：

转置一个三维数据的所有平面的命令

不过有趣的是，transpose 的默认 axes 参数（以及仅有的 a.T 运算模式）会调转索引顺序的方向，这与上述两个索引顺序惯例都不相符。

最后，还有一个函数能避免你在处理多维数组时使用太多训练，还能让你的代码更简洁——einsum（爱因斯坦求和）：

它会沿重复的索引对数组求和。在这个特定的例子中，np.tensordot(a, b, axis=1) 足以应对这两种情况，但在更复杂的情况中，einsum 的速度可能更快，而且通常也更容易读写——只要你理解其背后的逻辑。

如果你希望测试你的 NumPy 技能，GitHub 有 100 道相当困难的练习题：https://github.com/rougier/numpy-100。

你最喜欢的 NumPy 功能是什么？请与我们分享！

,