初一数学下册平行线知识点（初一数学下册相交线基础知识）

一、相交线

1.邻补角与对顶角

两直线相交所成的四个角中存在几种不同关系的角，它们的概念及性质如下表：

注意点：

⑴对顶角是成对出现的，对顶角是具有特殊位置关系的两个角；

⑵如果∠α与∠β是对顶角，那么一定有∠α=∠β；反之如果∠α=∠β，那么∠α与∠β不一定是对顶角

⑶如果∠α与∠β互为邻补角，则一定有∠α ∠β=180°；反之如果∠α ∠β=180°， 则∠α与∠β不一定是邻补角。

⑶两直线相交形成的四个角中，每一个角的邻补角有两个，而对顶角只有一个。

2.垂线

⑴定义：当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直， 其中的一条直线叫做另一条直线的垂线，它们的交点叫做垂足。

符号语言记作：

如图所示：AB⊥CD，垂足为 O

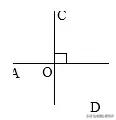
⑵垂线性质 1：过一点有且只有一条直线与已知直线垂直 (与平行公理相比较记)

⑶垂线性质 2：连接直线外一点与直线上各点的所有线段中，垂线段最短。简称：垂线段最短。

3.垂线的画法：

⑴过直线上一点画已知直线的垂线；

⑵过直线外一点画已知直线的垂线。

注意：①画一条线段或射线的垂线，就是画它们所在直线的垂线；②过一点作线段的垂线，垂足可在线段上，也可以在线段的延长线上。

画法：⑴一靠：用三角尺一条直角边靠在已知直线上，⑵二移：移动三角尺使一点落在它的 另一边直角边上，⑶三画：沿着这条直角边画线，不要画成给人的印象是线段的线。

4.点到直线的距离

直线外一点到这条直线的垂线段的长度，叫做点到直线的距离。应该结合图形进行记忆。

如图，PO⊥AB，同 P 到直线 AB 的距离是 PO 的长。PO 是垂线段。PO 是点 P 到直线 AB所有线段中最短的一条。 现实生活中开沟引水，牵牛喝水都是“垂线段最短”性质的应用。

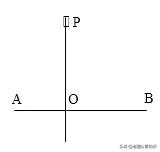
5.如何理解“垂线”、“垂线段”、“两点间距离”、“点到直线的距离”这些相近而又相异的概念。分析它们的联系与区别。

⑴垂线与垂线段

区别：垂线是一条直线，不可度量长度；垂线段是一条线段，可以度量 长度。

具有垂直于已知直线的共同特征。(垂直的性质)

⑵两点间距离与点到直线的距离

区别：两点间的距离是点与点之间，点到直线的距离 是点与直线之间。

都是线段的长度；点到直线的距离是特殊的两点(即已知点与 垂足)间距离。

⑶线段与距离

距离是线段的长度，是一个量；线段是一种图形，它们之间不能等同。

声明：本文来自“初中数学哥”，若涉及版权问题，请尽快联系删除！

,