等腰直角三角形中最值问题（直角三角形中利用等角三角函数值等比相似更方便实用）

73.在矩形PQRS中，PS=4PQ，点T是AD边上的动点，将△TPQ沿TQ翻折得△TWQ，作WX⊥PW，WX交PS于X，设PS=nPT.

（1）当W落在QR边上时，求n的值；

（2）当W落在矩形PQRS内部且△WXR为直角三角形时，求n的值.2

图1

翻折＝＞全等、垂直平分

（1）当W落在QR边上时，正方形PQWT＝＞n=4

（2）当W落在矩形PQRS内部＝＞∠XRW＜∠QRS=90°＝＞∠XRW＜90°（排除∠XRW=90°）

当△WXR为直角三角形时＝＞分两种讨论 ∠RWX=90°或∠WXR=90°

（1）如图2，当W落在QR边上时，∠PQW=∠PQR= 90°，

翻折＝＞∠QPT=∠QWT= 90°且PQ=QW

∴正方形PQWT＝＞PT=PQ＝＞PS=4PQ=4PT＝＞n=4

图2

（2）当W落在矩形PQRS内部＝＞∠XRW＜∠QRS=90°＝＞∠XRW＜90°

当△WXR为直角三角形时＝＞两种可能∠RWX=90°或∠WXR=90°

如图3，若∠RWX=90°，WX⊥PW＝＞∠PWR=180°＝＞W在对角线PR上

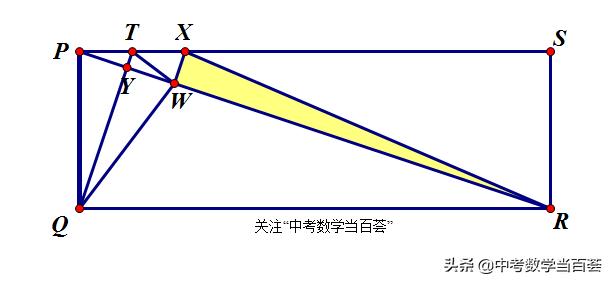
图3

矩形PQRS＝＞∠SPR＋∠QPR=90°且SR=PQ

翻折＝＞∠PQT＋∠QPR=90°

∴∠SPR=∠PQT＝＞tan∠SPR = tan∠PQT

＝＞SR：PS=PT：PQ＝＞PT=1/4PQ

PS:PT=4PQ: 1/4PQ=16＝＞PS=16PT＝＞n=16

设PQ=x，则PQ=4x，翻折＝＞TQ垂直平分PW

TY⊥PW，Y为PW中点，又XW⊥PW＝＞T为PX中点，设PT=m＝＞PX=2m

SX=4x－2m，SR=PQ=x

如图4，若∠WXR=90°，WX⊥PW＝＞PW∥XR＝＞∠XPW=∠SXR

图4

矩形PQRS＝＞∠XPW＋∠QPW=90°

翻折＝＞∠TQP＋∠QPW=90°

∴∠TQP=∠XPW=∠SXR＝＞tan∠TQP = tan∠SXR

＝＞PT:PQ=SR:XS＝＞m：x=x：（4x－2m）

＝＞x^2－4mx=－2m^2＝＞x^2－4mx＋4m^2=2m^2

＝＞（x－2m）^2=2m^2＝＞x－2m=√2m＝＞x=（2＋√2）m

＝＞4x=4（2＋√2）m＝＞PS=4（2＋√2）PT

＝＞n=4（2＋√2）=8＋4√2

（1）本题中，利用矩形性质:直角，对边平行且相等；利用翻折即轴对称，全等，垂直平分；

（2）主动点T在边PS上的特殊位置，决定从动点W相对于矩形PQRS的位置；

（3）利用特殊时刻，发现特殊位置关系：垂直或平行，角相等；

（4）在直角三角形中，利用等角的相应三角函数值相等，列比例式比利用相似对应边成比例更为方便。