中心极限定理成立的条件（中心极限定理的理解与证明）

图1

再进一步：

图2

注意，这里已经是将

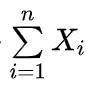
即随机变量之和作为一个变量看待。对图1中的分子分母都除以n之后，定理变成：

图2

图2中的变量又变成了样本的均值。

举例：假如现在要调查某个学校学生的政治成绩，要计算学生政治的平均成绩。要是去收集每个学生的成绩，然后加总，再除以学生总数，整个工作力度很大，成本也高。这时候中心极限定理就派上用场了，可以先从校园中随机的抽取50个人，然后计算这50个人的平均成绩，每个学生记为Xi,计算平均成绩;然后再随机的抽取的50个人，再计算平均成绩;一直这样随机的抽取，到最后进行了m次，一共得到m个平均成绩，中心极限定理说的就是这m个平均成绩的分布是正态分布，它们的均值就是该校学生政治的平均成绩。这里假设每个学生的成绩服从【0-100】间的均匀分布。

图3 m个不同平均成绩的概率分布

中心极限定理还有一点要注意，就是不管Xi 服从的是何种分布，只要它们相互独立且分布相同，只要样本量足够大，其均值最终都会服从正态分布。

再比如：从指数分布中提取样本

图4

从图4的指数函数曲线上每次随机抽取200个数据点，计算样本的均值，并将其绘制在直方图上。计算1000个这样的样本的均值，并将其画在直方图上，样本均值还是正态分布。所以，

中心极限定理意味着即使数据分布不是正态的，从中抽取的样本均值的分布也是正态的。

那么，中心极限定理如何证明呢？

首先要用到特征函数：

中心极限定理的证明：

图5

上面的变化用到了下面两个推导：

则图5中