碰撞追及问题（专题7.5碰撞爆炸）

一、碰撞过程研究

1. 碰撞过程的特征：“碰撞过程”作为一个典型的力学过程其特征主要表现在如下两个方面：

（1）碰撞双方相互作用的时间t一般很短；通常情况下，碰撞所经历的时间在整个力学过程中都是可以初忽略的；

（2）碰撞双方相互作用的力作为系统的内力一般很大。

2.“碰撞过程”的规律

正是因为“碰撞过程”所具备的“作用时间短”和“外力很小”（甚至外力为零）这两个特征，才使得碰撞双方构成的系统在碰撞前后的总动量遵从守恒定律。

3. 碰撞分类

从碰撞过程中形变恢复情况来划分：

（1）形变完全恢复的叫弹性碰撞；

（2）形变完全不恢复的叫完全非弹性碰撞；

（3）而形变不能够完全恢复叫非完全弹性碰撞。

从碰撞过程中机械能损失情况来划分：

（1）机械能不损失的叫弹性碰撞；

（2）机械能损失最多的叫完全非弹性碰撞；

（3）而一般的碰撞其机械能有所损失。

4. “碰撞过程”的特例

弹性碰撞作为碰撞过程的一个特例，它是所有碰撞过程的一种极端的情况：形变能够完全恢复；机械能丝毫没有损失。弹性碰撞除了遵从上述的动量守恒定律外，还具备：碰前、碰后系统的总动能相等的特征，即

讨论：当碰前物体2的速度不为零时

完全非弹性碰撞作为碰撞过程的一个特别，它是所有碰撞过程的另一种极端的情况：形变完全不能够恢复；机械能损失达到最大。正因为完全非弹性碰撞具备了“形变完全不能够恢复”。所以在遵从上述的动量守恒定律外，还具有：碰撞双方碰后的速度相等的特征，即

由此即可把完全非弹性碰撞后的速度

5. 制约碰撞过程的规律。

（1）碰撞过程遵从动量守恒定律

（2）碰撞后系统动能不增原则：碰撞过程中系统内各物体的动能将发生变化，对于弹性碰撞，系统内物体间动能相互转移？没有转化成其他形式的能，因此总动能守恒；而非弹性碰撞过程中系统内物体相互作用时有一部分动能将转化为系统的内能，系统的总动能将减小．因此，碰前系统的总动能一定大于或等于碰后系统的总动能

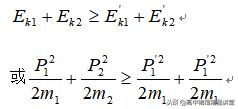
（3）碰撞前后的运动情况要合理

①若碰前两物体同向运动，则应有v后＞v前，碰后原来在前的物体速度一定增大，若碰后两物体同向运动，则应有v前′≥v后′。

②碰前两物体相向运动，碰后两物体的运动方向不可能都不改变。

【典例1】如图两滑块A、B在光滑水平面上沿同一直线相向运动，滑块A的质量为m，速度大小为2v0，方向向右，滑块B的质量为2m，速度大小为v0，方向向左，两滑块发生弹性碰撞后的运动状态是( )

A．A和B都向左运动 B．A和B都向右运动

C．A静止，B向右运动 D．A向左运动，B向右运动

【典例2】(多选)如图12所示，动量分别为pA＝12 kg·m/s、pB＝13 kg·m/s的两个小球A、B在光滑的水平面上沿一直线向右运动，经过一段时间后两球发生正碰，分别用ΔpA、ΔpB表示两小球动量的变化量。则下列选项中可能正确的是( )

A.ΔpA＝－3 kg·m/s、ΔpB＝3 kg·m/s

B.ΔpA＝－2 kg·m/s、ΔpB＝2 kg·m/s

C.ΔpA＝－24 kg·m/s、ΔpB＝24 kg·m/s

D.ΔpA＝3 kg·m/s、ΔpB＝－3 kg·m/s

E.ΔpA＝－1 kg·m/s、ΔpB＝1 kg·m/s

【典例3】两球A、B在光滑水平面上沿同一直线、同一方向运动，mA＝1 kg，mB＝2 kg，vA＝6 m/s，vB＝2 m/s.当A追上B并发生碰撞后，两球A、B速度的可能值是( )

A．vA′＝5 m/s，vB′＝2.5 m/s

B．vA′＝2 m/s，vB′＝4 m/s

C．vA′＝－4 m/s，vB′＝7 m/s

D．vA′＝7 m/s，vB′＝1.5 m/s

【典例4】如图在足够长的光滑水平面上，物体A、B、C位于同一直线上，A位于B、C之间。A的质量为m，B、C的质量都为M，三者均处于静止状态。现使A以某一速度向右运动，求m和M之间应满足什么条件，才能使A只与B、C各发生一次碰撞。设物体间的碰撞都是弹性的。

[方法规律]

碰撞问题解题策略

(1)抓住碰撞的特点和不同种类碰撞满足的条件，列出相应方程求解。

(2)可熟记一些公式，例如“一动一静”模型中，两物体发生弹性正碰后的速度满足：

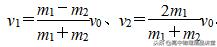
(3)熟记弹性

正碰的一些结论，例如，当两球质量相等时，两球碰撞后交换速度；当m1≫m2，且v20＝0时，碰后质量大的速率不变，质量小的速率为2v。当m1≪m2，且v20＝0时，碰后质量小的球原速率反弹。

【典例5】如图甲所示，物块A、B的质量分别是mA=4.0kg和mB=3.0kg. 用轻弹簧栓接，放在光滑的水平地面上，物块B右侧与竖直墙相接触. 另有一物块C从t=0时以一定速度向右运

动，在t=4s时与物块A相碰，并立即与A粘在一起不再分开，物块C的v-t图像如图乙所示.求：

（1）物块C的质量mC；

（2）墙壁对物块B的弹力在4 s到12s的时间内对对B的冲量I的大小和方向；

（3）B离开墙后的过程中弹簧具有的最大弹性势能Ep。

方法概述 对于以速度图像给出解题信息的问题，首先要在读懂图像的基础上，从速度图像中得出碰撞前后物体的速度， 然后利用动量守恒定律和相关物理规律列方程解答。

【典例6】一列火车共有n节车厢，各车厢之间间隙相等，间隙长度的总和为s。第一节车厢以速度v向第二节车厢运动，碰撞后两车厢不分开，直到n节车厢全部运动。忽略碰撞的时间，求：

（1）火车最后的速度和整个过程中损失的机械能；

【典例7】如图甲所示，ABC为一固定在竖直平面内的光滑轨道，BC段水平，AB段与BC段平滑连接。质量为m1的小球从高为处由静止开始沿轨道下滑，与静止在轨道BC段上质量为m2的小球发生碰撞，碰撞后两球的运动方向处于同一水平线上，且在碰撞过程中无机械能损失。求碰撞后小球m2的速度大小v2；

（2）碰撞过程中的能量传递规律在物理学中有着广泛的应用。为了探究这一规律，我们采用多球依次碰撞、碰撞前后速度在同一直线上、且无机械能损失的简化力学模型。如图乙所示，在固定光滑水平轨道上，质量分别为m1、m2、m3、···、mn-1、mn···的若干个球沿直线静止相间排列，给第1个球初动能Ek1，从而引起各球的依次碰撞。定义其中第n个球经过依次碰撞后获得的动能Ek与Ek1之比为第1个球对第n个球的动能传递系数k1n。

a． 求k1n。

b． 若m1=4m0，m3=m0，m0为确定的已知量。求m2为何值时，k13值最大。

方法概述 对于若干个球之间的碰撞，一般需要寻找递推关系。对于最值问题，一般需要利用数学求最值的知识。

二、爆炸模型

凡是内力瞬时做功，使系统机械能瞬时增大的都可以归纳为爆炸模型。在“爆炸”过程中，动量守恒，内力瞬时做功等于系统增大的机械能。

爆炸现象的三个规律

【典例8】如图所示，水平面上OM正中间有质量分别为2m、m的两物块B、C（中间粘有炸药），现点燃炸药，B、C被水平弹开，物块C运动到O点时与刚好到达该点速度为v0的小物块A发生迎面正碰，碰后两者结合为一体向左滑动并刚好在M点与B相碰，不计一切摩擦，三物块均可视为质点，重力加速度为g=10m/s2，求炸药点燃后释放的能量E。

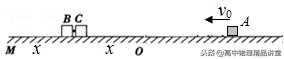
【典例9】从地面竖直向上发射一枚礼花弹，当上升速度为30 m/s时，距地面高度为150 m，恰好此时礼花弹炸开，分裂成质量相等的两部分，其中一部分经5 s落回发射点，求：

（1）另一部分炸开时的速度。

(2) 另一部分落点位置和落回地面的时间。

归纳总结

对于题述没有明确爆炸后弹片运动情况的需要先利用相关知识判断出弹片的运动情况。对于利用数学知识解一元二次方程得到的解，要判断结果的合理性，舍弃不合理数值。[来源:学|科|网]

三、反冲问题

1．对反冲现象的三点说明

(1)系统内的不同部分在强大内力作用下向相反方向运动，通常用动量守恒来处理。

(2)反冲运动中，由于有其他形式的能转变为机械能，所以系统的总机械能增加。

(3)反冲运动中平均动量守恒。

2. 讨论反冲运动应注意的三个问题:

(1) 速度的方向性

对于原来静止的整体,当被抛出部分具有速度时,剩余部分的反冲是相对于抛出部分来说的,两者运动方向必然相反。在列动量守恒方程时,可任意规定某一部分的运动方向为正方向,则反方向的这一部分的速度就要取负值。

(2) 速度的相对性

反冲运动的问题中,有时遇到的速度是相互作用的两物体的相对速度。但是动量守恒定律中要求速度是对同一惯性参考系的速度(通常为对地的速度)。因此应先将相对速度转换成对地的速度,再列动量守恒定律方程。

(3) 变质量问题

在反冲运动中还常遇到变质量物体的运动,如在火箭的运动过程中,随着燃料的消耗,火箭本身的质量不断减小,此时必须取火箭本身和在相互作用的短时间内喷出的所有气体为研究对象,取相互作用的这个过程为研究过程来进行研究。

【典例10】 一火箭喷气发动机每次喷出m ＝ 200 g 的气体，气体离开发动机喷出时的速度v ＝1000 m/s，设火箭质量M ＝ 300 kg，发动机每秒喷气20次。

(1) 当第三次气体喷出后，火箭的速度多大？

(2) 运动第1s末，火箭的速度多大？

【典例11】一质量为M的航天器，正以速度v0在太空中飞行，某一时刻航天器接到加速的指令后，发动机瞬间向后喷出一定质量的气体，气体喷出时速度大小为v1，加速后航天器的速度大小为v2，则喷出气体的质量m为( )

【典例12】 一个连同装备总质量为M=100kg的宇航员，在距离飞船x=45m处与飞船处于相对静止状态，宇航员背着装有质量为m0=0.5 kg氧气的贮气筒。筒上装有可以使氧气以v=50 m/s的速度喷出的喷嘴，宇航员必须向着返回飞船的相反方向放出氧气，才能回到飞船，同时又必须保留一部分氧气供途中呼吸用，宇航员的耗氧率为Q=2.5×10-4 kg/s，不考虑喷出氧气对设备及宇航员总质量的影响，则：

(1)瞬时喷出多少氧气，宇航员才能安全返回飞船？

(2)为了使总耗氧量最低，应一次喷出多少氧气？返回时间又是多少？

,