笛沙格定理的推广 笛沙格定理

笛沙格（1591—1661）法国数学家。射影几何学创始人之一，人们以他的名字命名的定理为：平面上有两个三角形，它们的对应顶点的连线交于一点，如果对应边或其延长线相交，则这三个交点共线，反之亦成立。两个三角形的对应顶点可以交于一点，但对应边或其延长线不一定相交，即有的平行，此定理是指如果相交，则三个交点共线。

如图，△ABC和△DEF，（与三角形的位置无关系，只要满足条件）对应顶点A和D，B和E，C和F相交于点O，AB，DE相交于P，AC，DF相交于Q，BC，EF相交于R，求证：P、Q、R三点共线。

分析：定理的证明，还是要用证三点共线的利器：梅毁涅劳斯定理（劳斯定理）来证明。那就要正确选择“梅氏”三角形，从结论来分析，若PQR为截线，可选择△ABC为“梅氏三角形”，这样就要证明：

这就要求我们把AP∶PB，BR∶CR，CQ∶QA建立比例式来证明上式成立，经过分析， AP∶PB，可选择△ABO作“梅氏三角形”，PED作“梅氏直线”来建立比例式；BR∶CR可选择△BCO，作“梅氏三角形”， EFR作“梅氏直线”来建立比例式；CQ∶QA可选择△CAO作“梅氏三角形”， QFD作“梅氏直线”。来建立比例式。

∵RFE分别交△BCO的边BC于R（R点分BC的两条线段为BR，CR）；CO于F（F分CO的两条线段是CF， FO），OB于E（E点分OB的两条线段是OE，EB），∴

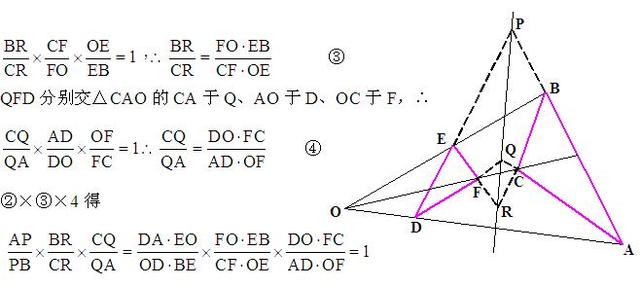
QFD分别交△CAO的CA于Q、AO于D、OC于F，∴

∵P、Q、R分别截AB于P，BC于R，CA于Q

∴由梅氏定理得：P、Q、R三点共线。