数学笔记平行线的性质（平行线及相关的数学发展---平行公设的改写）

就像人们通常的作为那样，发现一件事情存在问题之后，第一步的工作就是进行修正，对于欧几里得几何也是这样，数学家最初的工作是改写平行公设。为了进一步讨论方便，我们重新回顾一下《原理》的第五公设：

5. 同平面内一条直线和另外两条直线相交，若在某一侧的两个内角的和小于两个直角，则这两条直线经过无限延长后在这一侧相交。

这个公设的直接推论是：平行线的同旁内角之和为180度。雅典柏拉图学院的后期导师普罗克洛斯对整理和重新出版《原理》作出了重大贡献，资料表明，对平行公设提出质疑也是从他开始的。他希望通过一个平行线的定义来代替平行公设：

对于给定直线，称到这条直线距离保持一定的点的轨迹为这条直线的平行线。

这种定义的方法是可行的，但是普罗克洛斯的定义带来了一个更大的困难，如何能保证与直线距离保持一定的那些点的轨迹是一条直线呢？回忆欧几里得关于直线的定义：点同样地平放着的线，可能普罗克洛斯认为“距离保持一定”与“同样地平放着”是等价的，可是这个定义过分地借助了几何直观，在一般地意义上是不好理解地。

但是我们也应当看到，定义比公设具有更多地灵活性，因为公设多多少少要承担起放之四海而皆准的责任，而定义则限定了一个研究的范围，我们不需要顾及定义以外的情况。如果一定要给平行线下一个定义的话，如图（1）所示，我们可以尝试地给出下面的定义：

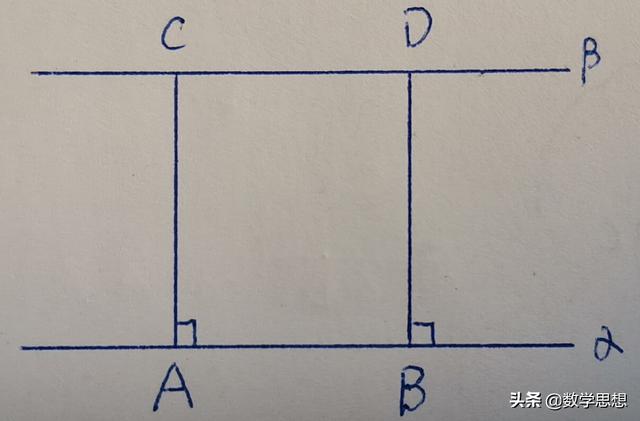
图（1）

在给定直线α上任取两点A和B，过这两点分别在直线上方作直线的垂线，取相同长度的点C和D，令过CD的直线为β，并称β是α的平行线。

由《几何作图及相关的数学发展---线段的四则运算和根式运算》中的讨论我们知道，上述定义中的几何作图是可能的。但这样定义又给我们带来了一个新的难题：如果在直线α上再取一个点A’，并用同样方法得到点C’，那么，是否能保证点C’也在直线β上呢？可以看到，如果要用定义的方法来解决平行公设，则需要我们在给出定义之前作更多的准备，我们将在后续《图形的量化》中详细地讨论这个问题。

由于定义不成功，人们开始思考，用一个新的命题来代替表述模糊的平行公设。其中，英国地质学家，数学家普莱费尔（1748-1819）给出了最为经典的平行公理：

过已知直线外一点，能且仅能作一条直线与已知直线平行。

这个公理蕴含着这两条直线永远不相交，在无穷远处也不相交。我们已经说过，这大概是欧几里得最不想涉及的，但是，这个公理可以保障图（1）中关于平行线的定义的合理性，因为如果C’不在直线β上，我们可以过两点C’和D再作一条直线γ，按照定义γ也是直线α的平行线，这就与公理矛盾了，因为α的这两条平行线都过点D。

为了教学的需要，现在我国中小学数学教材中把问题表述得更为繁杂。首先给出一个类似欧几里得给出的，不顾及存在性的平行线的定义：

称两条永远不相交的直线为平行线 （1）

这个定义对于孩子或许是直观的，但是这个定义是禁不起推敲的，我们应当清楚，要判断一条线是否永远是直的是非常困难的，是需要参照物的，这样的判断在无穷远处几乎是不可能的，何况现在又是两条直线，又要保证不相交。

然后，在普莱费尔的公设的基础上又给出一个类似定义的平行线的判定准则：

两条直线被第三条直线所截，如果同位角相等，则两条直线平行。

最后利用反证法，借助上述公理和判定准则可以证明平行线的性质：

两条直线平行则同位角相等。

这样，我们中学的数学用四个命题完成了对平行线的描述。我想，这样的描述远不如图（1）的定义简单明了。特别是，上述判定准则在论证体系中的功能是令人费解的，但是这个判定准则与性质却可以构成一个定理：

两条直线平行的充分必要条件是同位角相等。

既然这个命题是充分必要的，那么也可以作为定义。可是，又如何证明这个定义与（1）式所示最初的定义式等价的呢？如果要证明的话，则需要借助欧几里得最初的第五公设，即平行公设。问题绕了一圈，又回到了原点。看来，这种改写的方法不可能对平行线的问题得到更不性的改善。