平行四边形的面积知识结构图（平行四边形被分成三部分）

今天，数学世界给大家分享一道小学数学关于求图形面积的应用题，这题虽然很简单，但如果思路不正确，就肯定做不出来。解决此题的关键是要理解等底等高的三角形和平行四边形面积的大小关系，并利用比的意义。下面，我们就一起来看这道例题吧！

例题：（小学数学题）如图，一个平行四边形被分成甲、乙、丙三个三角形，已知甲的面积比丙多24平方厘米，乙的面积与丙的面积比是3：5，求这个平行四边形的面积是多少平方厘米？

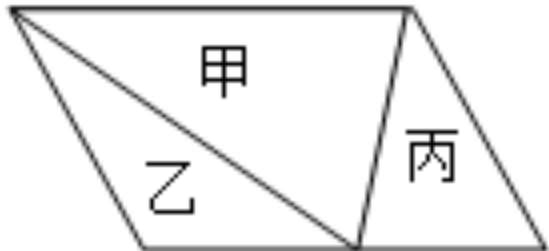
分析：由图可知，一个平行四边形被分成甲、乙、丙三部分，且甲的面积刚好是平行四边形的一半，所以乙的面积加上丙的面积是平行四边形的一半，所以甲的面积=乙的面积 丙的面积。

由于甲的面积比丙多24平方厘米，可以推出乙的面积就是24平方厘米，再根据“乙的面积与丙的面积比是3：5”即可推出丙的面积。乙的面积和丙的面积都求出后，即可求出平行四边形的面积。

解：由图可知，甲的面积刚好是平行四边形的一半，

甲的面积=乙的面积 丙的面积=平行四边形的一半

因为甲的面积比丙多24平方厘米，

所以乙的面积就是24平方厘米，

因为乙的面积与丙的面积比是3：5，

所以丙的面积是24×5/3=40（平方厘米）

平行四边形的面积是（24 40）×2=128（平方厘米）

答：这个平行四边形的面积是128平方厘米。

温馨提示，由于文章是作者一字一句打出来的，所以文中可能会出现一些不影响阅读的错误，还请大家谅解！郑重声明：这里全部文章均由猫哥原创，“数学世界”专注小学和初中数学知识分享。若朋友们还有不明白的地方或者有更好的解题方法，欢迎留言参与讨论。