六上数学圆的练习题讲解（26个考点配套例题详解）

圆的认识

1）圆心、半径、直径的含义、特点及表示方法

A.画圆时，注意别忘标圆心、半径、直径等，有数值的画尽可能标上。

作图题标准：信息完整、清楚、美观。

B.点拨：“画圆时，圆规两脚之间的距离是” ？半径。

例：画一个周长是12.56厘米的圆，圆规两脚间的距离应取（ ）。 A、2厘米 B、4厘米 C、3.14厘米

答案：已知周长求半径，选A.

2）圆心、半径的作用：圆心确定圆的位置，半径确定圆的大小。

3）在同一个圆内有什么知识：在同一个圆内，有无数条半径，有无数条直径，所有的半径都相等，所有的直径都相等。

4）在同圆或等圆内，直径、半径的关系

5）找圆心的方法：把圆对折，再对折,对折两次就能找到圆心。

6）对称性：圆是轴对称图形，直径所在的直线是圆的对称轴.（对称轴的本质是直线）圆有无数条对称轴。

7）圆的知识解解释现象。

圆的周长

1）定义：圆的周长：围成圆的曲线的长度叫做圆的周长。

2）圆周率：圆的周长总是直径的 3 倍多一些，这个比值是一个固定的数。我们把圆的周长和直径的商叫做圆周率，用字母 π 表示。圆周率是一个无限不循环小数。在计算时，通常取它的近似值：π ≈ 3.14。

例：下面正确的说法是（ ）。

π等于3.14。 B、周长相等的两个圆，面积也相等。C、半径是2厘米的周长和面积相等。

答案：A.π并不直等于3.14，只是为了计算方便，通常取它的近似值：π ≈ 3.14。B.对。C.只是数值相等，周长和面积是两种不同的量，单位都不一致，无所谓相等。

3）圆的周长公式：C= π d 或 C=2 π r

4）已知周长求直径、求半径

5）注意是求半圆的周长还是圆的周长的一半。半圆的周长等于圆的周长的一半加直径。半圆的周长与圆周长的一半的区别在于，半圆有直径，而圆周长的一半没有直径。

例：一个半圆形的花坛周长是30.84米，这个半圆形花坛的面积是(　　 )。

答案：2r＋π r =30.84，π取3.14，也就是2r＋3.14 r=30.84，左边一共有5.14个r，得30.84；那一个r就是6，即半径是6米.面积113.04平方米。

6）在同一个圆里，半径扩大或缩小多少倍，直径和周长也扩大或缩小相同的倍数。（像半径、直径和周长等长度维度，只能从一个方向上改变，故改变的倍数是倍数×1，而接下来的面积是从横和竖两个维度改变，故改变的倍数是倍数×倍数）

7）计算结果必记，在圆的面积计算里仍会用到！！！

1π＝3.14 2π＝6.28 3π＝9.42 4π＝12.56

5π＝15.7 6π＝18.84 7π＝21.98 8π＝25.12

9π＝28.26 10π＝31.4

根据右面的结果，也应立即反应出相应半径的值。

圆的面积

1）圆的面积：圆所占平面的大小叫圆的面积。

2）面积公式推导过程：

a.剪：把一个圆沿直径剪开，剪出36份或更多。

b.拼：拼成一个近似的长方形，

c.比：拼成的长方形的长相当于圆周长的一半，用字母（ π r）表示，宽相当于圆的半径，用字母（r）表示，

d.推导：因为长方形的面积=长×宽， 所以圆的面积= π r×r。 用字母表示为：Ｓ＝ πr2

例:把一个圆平均分成若干个小扇形，再拼成一个近似的长方形，这个长方形的长是12.56分米，这个圆的周长是（ ），面积是（ ）。

答案：这个长方形的长相当于圆周长的一半，即 π r=12.56分米，r=4分米。周长25.12分米，面积是50.24平方分米。

注意：在剪拼过程中，周长有什么变化：多出了两条宽，也即两条半径。

例：把一张圆形纸片沿半径平均分成若干份，拼成一个近似长方形，其周长（ ）。

A 等于圆周长 B 大于圆周长 C 小于圆周长 D 无法比较

答案：B

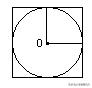
3）圆与正方形相结合：在一个正方形里画一个最大的圆，圆的直径等于正方形的边长。

例1：在一个边长为4分米的正方形里，画一个最大的圆，这个圆的直径为(　　 　 )分米，半径为(　 )分米，周长为(　　 )分米，面积为(　　 )平方分米。

答案：这个圆的直径为4分米，半径为2分米，周长为12.56分米，面积为12.56平方分米。

4）圆与长方形相结合：在一个长方形里画一个最大的圆，圆的直径等于长方形的宽。

例：在一个长9厘米，宽6厘米的长方形纸中，剪下一个最大的圆，纸片剩下部分的面积是多少平方厘米？

答案：半径3厘米，剩下部分的面积为：9×6-3.14×3×3=25.24（平方厘米）

5）环形面积：大圆的半径是 R， 小圆的半径是 r，环形的面积是 S= πR2－ πｒ2（其中大圆的半径=小圆的半径＋环的宽度，即R＝r＋环的宽度），注意：大圆直径比小圆直径多出什么呢？（2个环宽）

例：在一个半径为3米的圆形花坛外，围绕一周修一条1米宽的小路，这条小路的面积是多少平方米？

答案：大圆的半径是 4米，小圆的半径是3米，环形的面积是 S= πR2－ πｒ2=3.14×16－3.14×9，这里要注意千万别分别乘出得数，加大了运算量，而应该用乘法的意义来解，即16个3.14减去9个3.14，还剩7个3.14，从而得28.26平方米。

还有个注意：千万别算成3.14×（4-3）2

例：一个池塘的周长251.2米，池塘周围是一条5米宽的水泥路，在路的外侧围一圈栏杆。水泥路的面积是多少？栏杆长多少米？

答案：栏杆长，也即大圆的周长。

6）半圆面积.

7）在同一个圆里，半径扩大或缩小多少倍，面积扩大或缩小它的平方倍。（面积是从横和竖两个维度改变，故改变的倍数是倍数×倍数 ）

例1：在同一个圆里，半径扩大４倍，那么直径和周长就都扩大４倍，而面积扩大１６ 倍。

例2.大圆与小圆半径的比是4∶3，小圆面积与大圆面积的比是（ ）。

答案：16:9

例3：有大、小两个圆,小圆周长是37.68米，大圆直径是小圆直径的2倍，大圆的面积是多少？

答案：由"大圆直径是小圆直径的2倍"可以得出"大圆半径是小圆半径的2倍"，"大圆周长是小圆周长的2倍"，"大圆面积是小圆面积的4倍"等结论，那么只需算出大圆的面积从而除以4得到小圆的面积，或先用大圆的周长除以2，求出小圆的周长，再去求小圆的面积，最后求得：28.26平方米。

8）在周长相等的所有平面图形中，圆的面积最大。在面积相等的所有平面图形中，圆的周长最小。

例：用12.56米的铁丝围成一个正方形，正方形面积是（ ），如果把它围成一个圆，圆的面积是（ ）。

答案：周长相等的正方形和圆，求出的数值要与"在周长相等的所有平面图形中，圆的面积最大。"相符哦，正方形面积是9.8596平方米，圆的面积是12.56平方米.

9）注意与上题不同：

一个圆的直径等于一个正方形的边长，那么正方形面积大于圆的面积。用画图的方法理解：当圆的直径等于正方形的边长，正方形是能把圆包在里面的，完全不用计算得出。

10）计算，记住能减少很多运算量！

3.14*1*1=3.14 3.14*2*2=12.56 3.14*3*3=28.26 3.14*4*4=50.24

3.14*5*5=78.5 3.14*6*6=113.04 3.14*7*7=153.86 3.14*8*8=200.96

3.14*9*9=254.34 3.14*10*10=314

4.综合圆的周长和面积

1）需要厘清的几件事：

A.分针针尖走过的距离与分针扫过的面积，前者指周长，后者指面积

例：一个挂钟的时针长2.5厘米,一昼夜这根时针的尖端走了（ ）

A.15.7厘米 B. 31.4厘米 C.78.5厘米

答案：时针的尖端走了多远，在问周长，选A.

B.车轮滚过的一圈的距离是周长，压路车压过的是圆柱的侧面积（六下知识）

例：通过一座桥，直径是1.2米的车轮需转500圈，这座桥长多少米？（周长×500圈）

例：一辆压路机每分钟行驶15米，它压过的路面大约宽2米。压路机行驶25分钟，压过的路面面积是多少平方米？（圆柱的侧面积）

c.求阴影部分的周长，一定要先描出外沿。看出周长包含哪几部分。

图形的周长即围绕图形一周的线的长

例：如图中阴影部分图形的周长是（　　）cm．

A．16π B．8π 8 C．12π 8

答案：三部分长度组成：一个半径＋大圆周长的一半＋小圆周长的一半，选c.

例2：求阴影部分的周长。（单位：厘米）（8分）

第一幅图：周长为一整个圆的周长，第二幅周长为两个整圆的周长。

2）几个强调：

A.求图形面积时要有整体思想。

注意求阴影面积时，可以把多个部分圆合起来看成整圆，反之，有时也把整圆拆分成几个部分圆，部分圆一般是四分之一圆，二分之一圆等。

例：下面三幅图的阴影部分的面积相比较，________的面积大。 (　　　 )

(1)图(1)大 (2)图(2)大 (3)图(3)大 (4)同样大

答案：阴影面积都是正方形的面积减去一整个圆的面积，所以相等。

B.与钱相结合，选乘还是除。

例：一个圆形的桌面，直径为80厘米，现在要在桌面上安放一个同样大小的玻璃，求这个桌面玻璃的面积？如果玻璃每平方米价格为100元，这个玻璃要花多少钱？

点拨："玻璃每平方米价格为100元"是一份数，"桌面玻璃的面积"指一共有多少个这样的平方米，是几份数，想求总钱数就用乘法。

c.求阴影部分的面积题，常用的几种连辅助线方法等，图文表达起来太不方便，以后视频说。

最后要说，全手工打字，如果觉得对您有帮助，请不吝转发、收藏、点赞哦！感谢！

,