python矩阵基础（Python人工智能数学基础）

第1章 线性代数运算概述

1.1 什么是线性代数

线性（linear）指量与量之间按比例、成直线的关系，在数学上可以理解为一阶导数为常数的函数。

1.2 线性代数运算

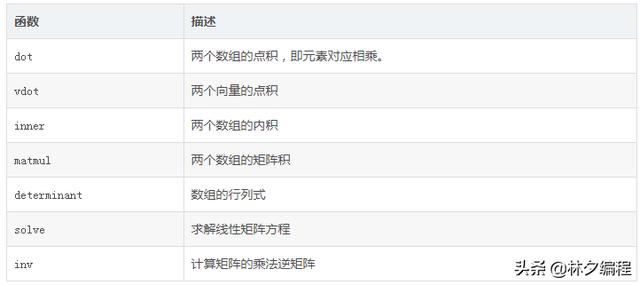
1.3 线性代数与深度学习的关系

深度学习中，存在大量向量和矩阵运算，矩阵运算的本质是并行的乘法和加法运算，如下图所示：

因此很有必要先熟悉一下向量运算和矩阵的运算。

第2章 向量与矩阵的定义2.1 什么是向量

在数学中，向量（也称为欧几里得向量、几何向量、矢量），指具有大小（magnitude）和方向的量。

（1）向量的空间几何意义：可以形象化地表示为带箭头、有方向的线段，实际上代表的是：空间中相对于原点的一个点！！！原点到给点的有向线段就是向量。

（2）向量的代数意义：在不同维度空间中的投影数值的序列。

如0维向量：几何意义是奇点或0点，代数表示：0；

如1维向量：几何意义是x轴上的一个点；代数表示为（A1）

如2维向量：几何意义是平面上的一个点；代数表示为（A1，W2）；其中a1和a2分别标识在x轴和y轴上的投影，即用x和y轴方向的投影的数值来表示向量。

如3维向量：几何意义是三维空间上的一个点；代数表示为（A1，A2, A3）；其中A1，A2，A3分别标识在x轴、y轴上、z轴上的投影数值，即用x、y、z轴方向的投影的数值来表示向量。

如N维向量：几何意义是n维空间上的一个点；代数表示为（A1，A2, A3，。。。。。An）；其中A1，A2，A3，An分别表示在n个维度方向上的投影数值。

也就是一个，一个特定的序列（A1，A2, A3，。。。。。An），代表了n维空间中的一个特定点，

Ai =0：表示该点，在第i维空间的投影值为0，也就是说该点在i维度空间是不可见的，也就是说该点对第i维度空间没有影响。

（3）在深度学习中的意义：包含n个维度特征的数据。

如0维向量：该数据没有任何特征。

如1维向量：该数据中包含1个维度的特征，如温度。

如2维向量：该数据中包含2个维度的特征，如温度，颜色

如3维向量：该数据中包含3个维度的特征，如温度，颜色，大小

如N维向量：该数据中包含n个维度的特征，如温度，颜色，大小，高度，长度，地域，国家信息，

Ai = 0：表示该数据与某个特征无关，输出与输入与某个特征无关 。

（4）向量与numpy

向量在Numpy中，体现在1维的数组中。

向量的维度，体现在1维数组中元素的个数，即1维矩阵中“列”的位数。

因此，向量的运算间的运算，就是1维数组间的运算。

2.2 什么是矩阵

在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合。

这m×n 个数称为矩阵A的元素，简称为元，数aij位于矩阵A的第i行第j列，称为矩阵A的(i,j)元，以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n，m×n矩阵A也记作Amn。

（1）矩阵的几何意义：m组n维向量的组合

（2）矩阵的代数意义：解线性方程组

（3）矩阵的深度学习意义：包含n个特征值的m组数据，通过这组数据，可以计算神经网络n个特征值的系数向量值。

2.3 向量与矩阵的关系

m组n维的向量就构成了矩阵。

第3章 数组的运算3.1· 向量内积：numpy.inner()

numpy.inner() 函数返回一维数组的向量内积（对应位相乘后累加）。

对于更高的维度，它返回最后一个轴上的和的乘积。

#实例 import numpy as np a = np.array([1,2,3]) b = np.array([0,1,0]) print (np.inner(a,b) # 等价于 1*0 2*1 3*0 # 输出结果为： # 2

#多维数组实例 import numpy as np a = np.array([[1,2], [3,4]]) print ('数组 a：') print (a) b = np.array([[11, 12], [13, 14]]) print ('数组 b：') print (b) print ('内积：') print (np.inner(a,b))

# 输出结果为： 数组 a： [[1 2] [3 4]] 数组 b： [[11 12] [13 14]] 内积： [[35 41] [81 95]] # 内积计算式为： 1*11 2*12, 1*13 2*14 3*11 4*12, 3*13 4*14

3.2 向量的点乘运算：numpy.dot()

对于两个一维的数组，计算的是这两个数组对应下标元素的乘积和(数学上称之为内积)；

对于二维数组，计算的是两个数组的矩阵乘积；

对于多维数组，它的通用计算公式如下，即结果数组中的每个元素都是：数组a的最后一维上的所有元素与数组b的倒数第二位上的所有元素的乘积和： dot(a, b)[i,j,k,m] = sum(a[i,j,:] * b[k,:,m])。

numpy.dot(a, b, out=None)

参数说明：

• a : ndarray 数组
• b : ndarray 数组
• out : ndarray, 可选，用来保存dot()的计算结果

#实例1 import numpy.matlib import numpy as np a = np.array([1,2,3,4]) b = np.array([11,12,13,14]) c = np.dot(a,b) #点乘：按相同小标相乘 print(c) #输出结果： [11 24 39 56]

计算式为：

[1*11, 2*12, 3*13, 4*14]]

#实例2 import numpy.matlib import numpy as np a = np.array([[1,2],[3,4]]) b = np.array([[11,12],[13,14]]) c = np.dot(a,b) #点乘：按相同下标相乘 print(c) #输出结果： [[37 40] [85 92]]

计算式为：

[[1*11 2*13, 1*12 2*14],[3*11 4*13, 3*12 4*14]]

第4章 矩阵运算4.1 矩阵的标量运算

4.2 矩阵的加减运算

4.3 矩阵的点乘运算

4.4 矩阵叉乘：numpy.matmul

该函数返回两个数组的矩阵乘积。 虽然它返回二维数组的正常乘积，但如果任一参数的维数大于2，则将其视为存在于最后两个索引的矩阵的栈，并进行相应广播。

另一方面，如果任一参数是一维数组，则通过在其维度上附加 1 来将其提升为矩阵，并在乘法之后被去除。

对于二维数组，它就是矩阵乘法：

实例 import numpy.matlib import numpy as np a = [[1,0],[0,1]] b = [[4,1],[2,2]] print (np.matmul(a,b)) 输出结果为： [[4 1] [2 2]]

————————————————

感谢大家的支持和喜欢，小编会每天分享更多Python学习的干货知识给大家，所以大家别忘了关注小编哦。

版权声明：本文为CSDN博主「文火冰糖的硅基工坊」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。

原文链接：https://blog.csdn.net/HiWangWenBing/article/details/119301224

,