虚数的本质（关于虚数的5个有趣的事实）

虚数是一个抽象的概念，但是虚数对我们精确描述我们的宇宙是必不可少的。它的存在让很多公式变得简洁而优美。

对于数学家来讲“世界上可能没有足够多的爱能拿来表达虚数的存在”。很多时候，如果你想精确地描述你生活的这个宇宙，你需要跳出传统思维的束缚。在20世界早期，物理学的两个重大突破——相对论和量子力学对数学的需求远远超过了实数的范畴。从那以后，复数数学的发展开始在我们理解这个宇宙中发挥重要的作用。

复数包含两个部分，实数部分和虚数部分。当我们最开始接触数学的时候，我们基本上是按照下面的顺序逐件扩展的：

• 可数的数：1，2，3，4……等等。这些数字是无限多的

• 整数：0，1，2，3……等等，跟可数的数相比，这里多了数字0

• 所有的整数：……，-3，-2，-1，0，1，2，3，……。这里我们又包含进去了负数

• 有理数：很多数可以表示成两个整数的除法形式。因此有理数包含了所有的整数和所有有限重复的小数。

• 实数：除了有限重复的小数之外还有无限重复小数，即无理数例如自然数e，圆周率π等。有理数和无理数的和为无理数，而两个无理数的和则可能为有理数。

正数的开方是实数，而负数的开方呢？之前并没有很好地定义。直到虚数的概念提出来以后，这个问题才得以解决。虚数和实数的不同之处就在于它们后面都乘了一个“i”，即-1的开方。数字也可以是复数，即它们即有实数部分(a)也有虚数部分(b)，可以表示成a bi的形式。

两边同时平方我们得到：

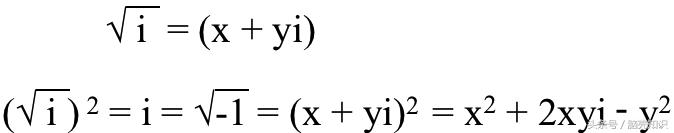
我们把实数和虚数的部分对应起来：

继续求解：

因此我们可以得到：

我们可以看到，实际上i的开方是有两个解的：

这个让i有了下面一个有意思的性质

2、i的任何次开方都有多个结果，开N次方就有N个不同的解

对于正数而言，你最多可能只有两个解。但是对虚数而言，解的个数可能跟开方的次数一样多了。

例如：

对i开3次方，4次方和5次方，分别可以得到3个，4个和5个解。例如i开3次方可以得到：

3、虚数分数中i位于分子位置还是位于分母位置对最后的结果影响很大

对实数除法-1/1和1/-1的结果是一样的，但是对虚数而言结果就不一样了，例如：

它的值就为-i，而不是i

在复数运算中i的结合顺序非常重要，如果运用不当可能导致错误的结果，例如：

4、e，π和i三者可以统一在一起

坐标系可以是标准的由x轴和y轴描述的正交坐标系，也可以是半径r和角度θ描述的极坐标系。如图：

但是如果你用实数和虚数来代表x轴和y轴，那么你可以得到：

上面的公式在角度为180度即-1的位置的时候我们可以得到一个非常优美的结果：

这个公式就是有名的欧拉公式，它在很多复杂分析中都广泛应用。

5、i^i或者i的i 次方，是100%的实数

对上面的欧拉公式我们考虑i的位置，即角度为90度：

两边都计算i次方：

我们得到：

这个值大约为0.20788，是一个实数。

虚数i代表的含义非常值得人们去深思，就像中国的太极哲学一样，实数和虚数虚虚实实转化演绎者我们生活的宇宙。

---

每天思考一分钟

脑壳（naokr.com）——思考很快乐

,