数学圆的最值问题解题方法（盘点圆的最值问题求解策略）

圆是数学中优美的图形，具有丰富的性质。由于其图形的对称性和完美性，很多与圆有关的问题都可以运用圆的图形性质，利用数形结合求解。

而圆中的最值问题综合性较强，有一定难度，在中考为热点难点题型，经常出现，下我们就来总结一下这类问题的一般解法。

​策略一：利用直径是圆中最大的弦

1.（2020秋•东台市期中）如图，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB＝30°，点E、F分别是AC、BC的中点，直线EF与⊙O交于G、H两点，若⊙O的半径为8，则GE FH的最大值为（　　）

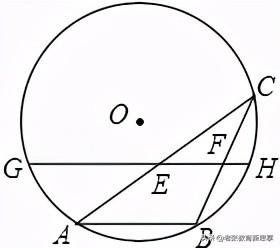
A．8 B．12 C．16 D．20

【解答】：连接OA、OB，如图所示：

∵∠ACB＝30°，∴∠AOB＝2∠ACB＝60°，

∵OA＝OB，∴△AOB为等边三角形，

∵⊙O的半径为8，∴AB＝OA＝OB＝8，

∵点E，F分别是AC、BC的中点，∴EF＝1/2AB＝4，

要求GE FH的最大值，即求GE FH EF（弦GH）的最大值，

∵当弦GH是圆的直径时，它的最大值为：8×2＝16，

∴GE FH的最大值为：16﹣4＝12．

故选：B．

​策略二：过圆内一点的弦中，与过该点的直径垂直的弦最短.

2.（2020秋•沭阳县期中）如图，在平面直角坐标系xOy中，以原点O为圆心的圆过点A（13，0），直线y＝kx﹣3k 4（k≠0）与⊙O交于B、C两点，则弦BC的长的最小值为_______．

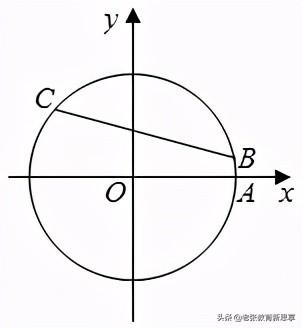
【解析】：连接OB，

∵直线y＝kx﹣3k 4必过点D（3，4），

∴最短的弦CB是过点D且与该圆直径垂直的弦，

∵点D的坐标是（3，4），

∴OD＝​​＝5，

∵以原点O为圆心的圆过点A（13，0），

∴圆的半径为13，∴OB＝13，

∴BD＝​​＝12，

∴BC＝2BD＝24，

∴BC的长的最小值为24；

故答案为：24．

策略三：弓形上的点到弦的距离中，最大距离是该弧的中点到弦的距离（或者过圈心的一条垂线段）.

3.（2011•南昌中考题）如图，已知⊙O的半径为2，弦BC的长为2√3，点A为弦BC所对优弧上任意一点（B，C两点除外）．

（1）求∠BAC的度数；

（2）求△ABC面积的最大值．

（参考数据：sin60°＝√3/2，tan30°＝√3/3．）

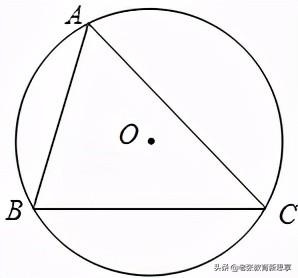
【解析】（1）连接OB、OC，作OE⊥BC于点E，由垂径定理可得出BE＝EC＝√3，在Rt△OBE中利用锐角三角函数的定义及特殊角的三角函数值可求出∠BOE的度数，再由圆周角定理即可求解∠BAC＝60°;

（2）因为△ABC的边BC的长不变，所以当BC边上的高最大时，△ABC的面积最大，此时点A落在优弧BC的中点处．

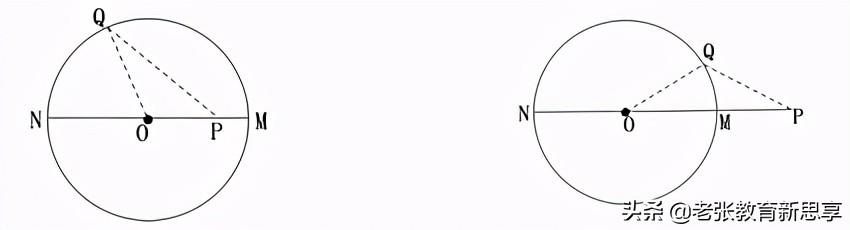
策略四：如图，若点P不在OO上，射线OP交圆O于M，射线OP的反向延长线交OO于N，则点P到圆上各点中，PM的长最小，PN的长最大。

4.如图，⊙O的直径为4，C为⊙O上一个定点，∠ABC＝30°，动点P从A点出发沿半圆弧AB向B点运动（点P与点C在直径AB的异侧），当P点到达B点时运动停止，在运动过程中，过点C作CP的垂线CD交PB的延长线于D点．

（1）在点P的运动过程中，线段CD长度的取值范围为_____-．

（2）在点P的运动过程中，线段AD长度的最大值为______．

【解析】：（1）如图1中，

∵AB是直径，∠ABC＝30°，AB＝4

∴∠ACB＝90°，∠A＝∠P＝60°，AC＝2，

∵CD⊥PC，

∴∠PCD＝90°，CD＝PC•tan60°，

∵PC的最小值＝AC＝2，PC的最大值为直径＝4，

（2）如图2中，

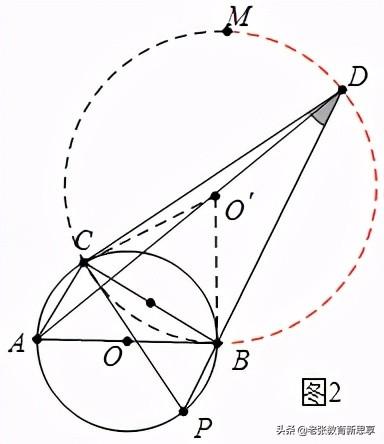
∵在Rt△PCD中，∠PCD＝90°，∠P＝60°，

∴∠PDC＝30°，

∴点D在以BC为弦的⊙O′（红弧线）上运动，

∴当A、O′、D共线时，AD的值最大．连接CO′、BO′．

∵∠BO′C＝2∠CDB＝60°，O′C＝O′B，

∴△O′BC是等边三角形，

策略五：如下图，直线L与圆O相离，线段OP⊥L，垂足为P，交O0于点M，PO的延长线交圆O于点N，则圆O上各点到直线L的距离中，最小距离是PM的长，最大距离是PN的长.

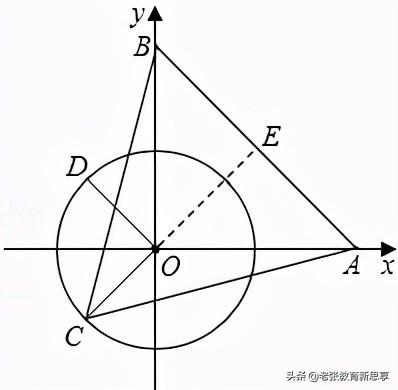
5.在平面直角坐标系xOy中，已知点A（6，0），点B（0，6），动点C在以半径为3的⊙O上，连接OC，过O点作OD⊥OC，OD与⊙O相交于点D（其中点C、O、D按逆时针方向排列），连接AB．

（1）当OC∥AB时，∠BOC的度数为_______；

（2）连接AC，BC，当点C在⊙O上运动到什么位置时，△ABC的面积最大？并求出△ABC的面积的最大值.

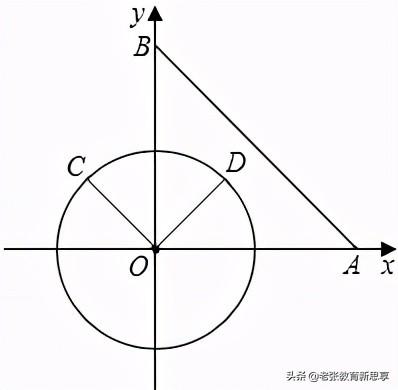
【解析】（1）根据点A和点B坐标易得△OAB为等腰直角三角形，则∠OBA＝45°，由于OC∥AB，所以当C点在y轴左侧时，有∠BOC＝∠OBA＝45°；当C点在y轴右侧时，有∠BOC＝180°﹣∠OBA＝135°；

（2）∵△OAB为等腰直角三角形，

∴AB＝√2OA＝6√2，

∴当点C到AB的距离最大时，△ABC的面积最大，

过O点作OE⊥AB于E，OE的反向延长线交⊙O于C，如图，此时C点到AB的距离的最大值为CE的长，

策略六：直线L与半径为r的圆相离，圆心O到直线L的距离为d，点P为直线L上任意一点，PA与圆O相切于点A，则PA的最小值是​，此时∠OPA最大.

6.​如图，在Rt△AOB中，OA＝OB＝3√2，⊙O的半径为1，点P是AB边上的动点，过点P作⊙O的一条切线PQ（点Q为切点），则切线PQ的最小值为______．

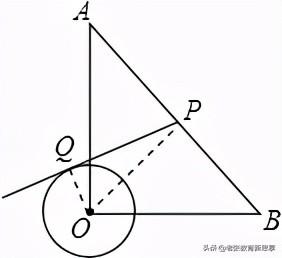
【解析】：连接OP、OQ．

∵PQ是⊙O的切线，

∴OQ⊥PQ；

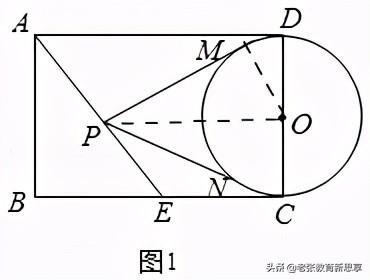
7.（2020秋•宜兴市期末）如图，在矩形ABCD中，CD是⊙O直径，E是BC的中点，P是直线AE上任意一点，AB＝4，BC＝6，PM、PN相切于点M、N，当∠MPN最大时，PM的长为______．

【分析】先判断出OP⊥AE时，∠MPN最大，判断出△ABE≌△GCE，求出CG＝4，再用勾股定理求出AE＝5，再判断出△ABE∽△GPO，求出OP，最后用勾股定理求解，即可得出结论．

【解答】：如图1，∵四边形ABCD是矩形，

∴CD＝AB＝4，

连接OP，OM，

∵PM，PN是⊙O的切线，

∴∠OPM＝1/2∠MPN，

要∠MPN最大，则∠OPM最大，

∵PM是⊙O的切线，

∴∠OMP＝90°，

在Rt△PMO中，OM＝OD＝1/2CD＝2，

∴sin∠OPM＝OM/OP=2/OP，

∴要∠OPM最大，则OP最短，

即OP⊥AE，

如图2，延长DC交直线AE于G，

∵四边形ABCD是矩形，

∴∠B＝90°＝∠ECG，AB∥CD，

∴∠BAE＝∠G，

∵点E是BC的中点，

∴BE＝1/2BC＝3，

∴△ABE≌△GCE（AAS），

∴CG＝AB＝4，

∵CD是⊙O的直径，

∴OC＝1/2CD＝2，

∴OG＝OC CE＝6，

在Rt△ABE中，AB＝4，BE＝3，

∴AE＝5，

∵∠OPG＝90°＝∠B，∠G＝∠BAE，

∴△ABE∽△GPO，

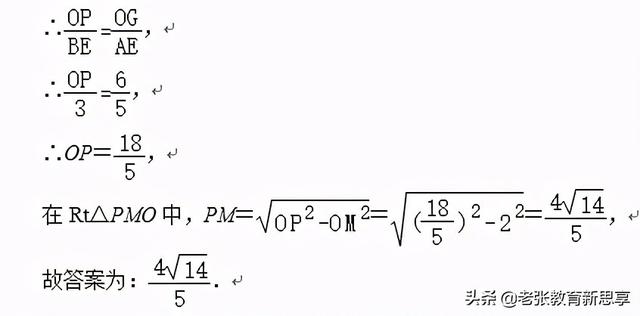
策略七：弦与弦心距的关系：弦心距越大，弦越小；弦心距越小，弦越大。

弓形的弦与所对的圆周角的关系：圆周角越大，所对的弦越大。

策略八：利用将军饮马模型

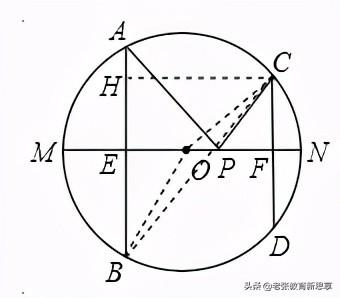
9.（2014•张家界中考题）如图，AB、CD是半径为5的⊙O的两条弦，AB＝8，CD＝6，MN是直径，AB⊥MN于点E，CD⊥MN于点F，P为EF上的任意一点，则PA PC的最小值为______．

【分析】A、B两点关于MN对称，因而PA PC＝PB PC，即当B、C、P在一条直线上时，PA PC的最小，即BC的值就是PA PC的最小值

【解答】：连接OB，OC，作CH垂直AB于H．

不难发现，中考考题考的不是难度，而是思维。知识是载体，素养是目标。通过如此专题复习课中，我们除了要求学生掌握基本知识、基本技能之外，还需要学生掌握基本的数学思想，积累活动经验，因此我们需要一题多解、一题多变，并让学生注意一些比较相似的题目的区别与联系，避免就题讲题，让学生陷入题海战术。

因此，需要教师在课堂中与学生一起进行总结。构建完整的知识体系，务必灵活地运用知识解决实际问题。把复习的重点知识与解题的方法进行总结提升，让学生慢慢具备触类旁通、上下贯通的能力。

,