解析几何中的三角形（几何问题三角形全面剖析）

几何问题是近几年省考考察的内容之一，而其中对于三角形的考察，又受考官青睐。今天，中公教育带领各位考生一起来全面学习一下三角形的相关考点。

一、构成条件：两边之和大于第三边，两边之差小于第三边。

【例题1】若一个三角形的所有边长都是整数，其周长是偶数，且已知其中两边长分别为10和2000，则满足条件的三角形总个数是：

A.10 B.7 C.8 D.9

【中公解析】D。已知两边均为偶数，则第三边也为偶数。根据构成条件，1990<第三边<2010，满足的有1992、1994、1996、1998、2000、2002、2004、2006、2008，共有9组不同的三角形。故本题答案为D。

二、三角形面积：

【例题2】如图，在长方形ABCD中，已知三角形ABE、三角形ADF与四边形AECF的面积相等，则三角形AEF与三角形CEF的面积之比是：

A.5：1 B.5：2 C.5：3 D.2：1

【中公解析】A。由于长宽不确定，具有任意性，可设特值。将长方形ABCD视作为特殊的长方形-正方形。同时，因为其中三个区域面积相同，故总面积可设为3的倍数。

不妨设AD=3，DC=3,总面积为9.所以△ADF面积=

×总面积=3.因为AD=3，所以DF=2，则FC=1.同理△ABE面积=3，AB=3,则BE=2，则EC=1。

所以，

故△AEF与△CEF的面积比为5：1.故本题答案为A。

三、直角三角形

(1)勾股定理：直角三角形的两条直角边的平方和等于斜边的平方。如图，记作

(常用勾股数：3n、4n、5n，n为正整数)

(2)特殊直角三角形边长比：

【例题3】一艘游轮在海上匀速航行，航向保持不变。上午8时在游轮的正东方30海里处有一灯塔。上午10时30分该灯塔位于游轮的正南方40海里处，则在该时段内，游轮与灯塔距离最短的时刻是( )

A.8时45分 B.8时54分 C.9时15分 D.9时18分

【中公解析】B。距离最短时，游轮与灯塔的连线即为三角形的高。根据勾股定理，可得AB=50。根据常用勾股数(3n，4n，5n)，结合三边比例，易知CD=24。进而可知AD=18。故运动时间为150×

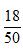
=54分钟。

四、三角形相似

1、相似的判定条件

(1)三角对应相等，两个三角形相似(AAA)

(2)两边对应成比例且夹角相等，两个三角形相似(SAS)

(3)三边对应成比例，两个三角形相似(SSS)

2、常用相似性质：

(1)相似三角形的对应边成比例;

(2)相似三角形的周长比等于相似比;

(3)相似三角形的面积比等于相似比的平方。

【例题4】某市规划建设的4个小区，分别位于直角梯形ABCD的4个顶点处(如图)，AD=4千米，CD=BC=12千米。欲在CD上选一点S建幼儿园，使其与4个小区的直线距离之和为最小，则S与C的距离是：

A.3千米 B.4千米 C.6千米 D.9千米

【中公解析】D。找到A点关于镜面CD的镜像，容易得到△A'DS与△SCB相似，故A'D：BC=SD：SC=1：3。所以SC=9.

五、三角形重心

1.重心：三角形三边中线的交点

2.性质：重心到顶点的距离与重心到对边中点的距离之比为2：1

【例题5】如图，A-BCD是棱长为3的正四面体，M是棱上的一点，且MB=2MA，G是三角形BCD的重心，动点P在棱BC上，则PM PG的最小值( )

【中公解析】B。展开图如图所示，因为G为重心，故BG为中线，也为正三角形的角平分线，故∠GBP为30°，且∠MBP为60°，容易发现∠MBG为直角。重心到顶点的距离与重心到对边中点的距离之比为2：1，则

根据勾股定理，故

【中公解析】B。距离最短时，游轮与灯塔的连线即为三角形的高。根据勾股定理，可得AB=50。根据常用勾股数(3n，4n，5n)，结合三边比例，易知CD=24。进而可知AD=18。故运动时间为150×

,