数学著名定理证明（绚丽经典的名定理）

法国著名数学家庞加莱曾说："能够作出数学发现的人，是具有感受数学中的秩序、和谐、对称、整齐和神秘美等能力的人。"

美的最大特征是具有感性形象。自然界总是以其悦耳的声音、绚烂的色彩、突兀的形式呈现它的多姿，艺术是通过典型的形象来博得人们的赞美，数学的美则表现在严谨的理论结构、简洁明快的数学语言、应用广泛的思想方法，基本特征是简洁性、对称性、统一性、奇异性、思辨性。古代埃及人就认为：圆，是神赐给人的神圣图形。

其实18000年前的山顶洞人用一种尖状的石器来钻孔，一面钻不透，再从另一面钻。石器的尖是圆心，它的宽度的一半就是半径，这样以同一个半径和圆心一圈圈地转就可以钻出一个圆的孔。

到了陶器时代，许多陶器都是圆的。圆的陶器是将泥土放在一个转盘上制成的。

6000年前，半坡人就已经会造圆形的房顶了。古代人还发现圆的木头滚着走比较省劲。后来他们在搬运重物时，就把几段圆木垫在重物的下面滚着走，这样就比扛着走省劲得多。

大约在6000年前，美索不达米亚人，做出了世界上第一个轮子——圆的木轮。

约在4000年前，人们将圆的木轮固定在木架上，这就成了最初的车子。但会作圆并且真正了解圆的性质，却是在2000多年前，是由我国的墨子给出圆的概念的："一中同长也。"意思是说，圆有一个圆心，圆心到圆周的长度都相等。这个定义比希腊数学家欧几里得提出的时间早100年。

圆，是人类最钟爱的几何造型之一圆可以象征圆满，完美，也有圆润和谐的寓意。圆是一种"完美"的图形，与圆相关的定理简洁、别致，给人美感，令人陶醉，使人赞叹。如图，圆的面积公式、扇形面积公式、扇环面积公式如此相似，展现了数学公式的统一之美。

统一性既是数学家追求的目标之一，又是数学美的特征之一统一性能帮助人们既关注细节，又把握整体，并产生伟大的发现．

当一个轮子在一条直线上平稳地滚动，轮子上的一个固定点所留下来的轨迹曲线叫摆线）１7世纪，总更据发现了摆线的学时性，设计出有钟摆的时钟，摆线因此而得名。伽利略发现了与摆线相关的重要结论：摆线弧长是轮子直径的4倍，摆线拱形面积是轮子面积的3倍。

托勒密定理：圆内接四边形两条对角线的乘积等于两对对边乘积之和。

托勒密定理的证明：

已知：四边形ABCD内接于圆，如图，求证：AB·CD BC·AD=AC·BD.

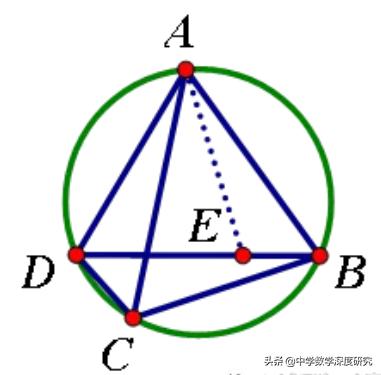
证明：在∠BAD内作∠BAE=∠CAD，交BD于E。因∠ABE=∠ACD，所以△ABE∽△ACD，从而AB·CD =AC·BE ①；

易证△ADE∽△ACB，所以BC·AD=AC·DE ②；

1 ②得AB·CD BC·AD=AC·BD。

例2.蝴蝶定理

已知：过圆O的弦PQ的中点M任作两条相交弦AB、CD，联结AC、BD分别与PQ交于E和F。

求证：ME＝MF.

根据维基百科，此结论1803年被提出，1944年被命名为蝴蝶定理，确实本图形形状酷似一只翩翩起舞的蝴蝶。此题图形简洁、结论优美，证明却殊为不易。所以此题一经披露，就引起了众多关注，也出现了多种证明，常见的有10多种。最早见于1815年《男士日记》,近年来，此定理又载沉载浮，出现了一些新的证明，分蘖出新的变种，并在竞赛及练习中时隐时现。本系列文章准备系统梳理此定理的经典证明，挖掘其本质，详细介绍各种变式，并结合最新题目展示其应用。第一篇文章准备先介绍本定理的五种典型证法。

本定理证明的思路主要是两类:一类是纯几何方法，另一类是计算。计算方法又大概分为两类：三角计算（面积法、Menelaus定理、交比等）、解析法。

纯几何方法一

思路分析1：看到圆及中点M想到垂径定理，两边元素相对分散，考虑到将C关于OM对称到C'，倒角发现MBC'F共圆，然后利用全等即可。

证明1：作弦CC'∥PQ，联结C'M、C'F。

则C、C'关于OM对称，故∠FMC'=∠MC'C=∠MCC'=∠DBC',故M、B、C'、F四点共圆，故∠F C'M=∠ABD=∠ECM,

又CM=C'M, ∠FMC'=∠EMC,则△CME≌△C'MF(ASA),故ME=MF。

纯几何方法二

思路分析2：显然OM⊥PQ，欲证ME=MF,即证△OME≌△OMF。显然△AMC∽△DMB，由对称性想到垂径定理，取AC、BD中点，从而得到共圆及等角，即得证。

证明2：联OM，由垂径定理，OM⊥PQ。再作OS⊥AC于S，OT⊥BD于T，

联结OE、OF、MS、MT。由垂直得MESO及MFTO四点共圆，

则∠MOE＝∠MSE，∠MOF＝∠MTF，

而由△AMC∽△DMB及S、T为中点，

得∠MSA＝∠MTD(相似三角形对应角相等)，

∴ ∠MOE＝∠MOF，由此Rt△OME≌Rt△OMF（ASA），故ME＝MF。

例3.西姆松线

过三角形外接圆上异于三角形顶点的任意一点作三边或其延长线上的垂线，则三垂足共线。这条线称为西姆松线。

如图，P在△ABC的外接圆上，PD、PE、PF分别垂直于AB、BC、CA，垂足为D、E、F，则D、E、F共线。

证明：∵∠PFA=∠PDA=90°，∴A、D、F、P四点共圆，

∴∠PFD ∠BAP=180°，∴∠PFC=∠PEC=90°，

∴C、E、P、F四点共圆。∴∠PFE=∠BAP，

∴∠PFE=∠BAP，∴∠PFD ∠PFE=180°。

∵A、B、C、P四点共圆，∴D、E、F三点共线。

与圆相关的优美定理精彩纷呈，如：

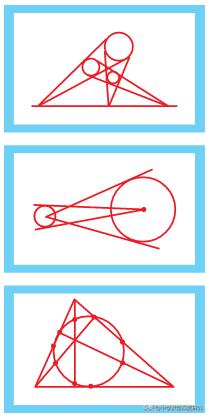
蒙日三圆定理：

如图，三个大小不等的圆中，任意两个圆的两条外公切线都相交于一点，这三个交点共线。这是法国数学家蒙日证明的定理。

眼球定理：

如图，过两个圆的圆心分别作另一个圆的切线，则切线与两圆相交的交点之间的线段相等。

九点共圆：

如图，三角形各边中点、三条高的垂足、各顶点与垂心之间的中点，这九点共圆。

自古希腊数学家毕达哥拉斯提出"整个世界就是数的和谐"命题后，数学美就成为许多数学家、科学家的孜孜追求。

张奠审教授曾提出欣赏数学美的四个层次：美观、美好、美妙、完美。任意三角形的三条高（三条中线、三条角平分线）交于一点，抛物线可用方程y=ax² bx c刻画，面对一个挑战性的数学问题，在我们冥思苦想，"山重水复疑无路"之时，忽然茅塞顿开，"柳暗花明又一村"，经历怦然心动、豁然开朗、悠然心会的心路历程，必然感受到的是成功的喜悦和心灵的愉悦，这就是数学美的第三个层次—美妙。

一个学生，如果在挥汗耕耘后，满脑子仍然是抽象的理论、干巴的公式、乏味的定理，而不能透过公式、定理、符号去体验和捕捉数学的神奇与优美，那将是一种遗憾。

一个学生，如果能从数学学习中体验到自然的哲理与诗意，领悟到自然的和谐与秩序，那么必然情灵摇荡，胸襟开阔。

德国著名物理学家海森堡曾说："在精密科学中，丝毫不亚于在艺术中，美是启发和明晰的最重要的源泉。我感到，透过原子现象的外表，我看到了一个美丽的内部结构。当想到大自然如此慷慨地将珍贵的数学结构展现在我眼前时，我几乎陶醉了"。

,