相术干货（你可能遇到了假的更相减损术）

旧日好友发过来一道题请教：请把1、2、3、4、5、6、7、8、9九个数字组成不重复的四位数和五位数，使得：

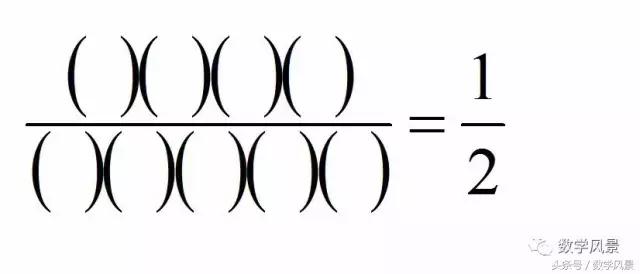
着实费了小编一番功夫，最后得到一个答案：

实际上这个有趣的数学问题并不是空穴来风，它被称为“塞姆罗德的书架趣题，”来源于美国著名趣题大师塞姆罗德，相传在塞姆罗德小的时候，有人送给他一套《英国历史》，共九卷。他随意地把这套书分放在双层书架上，上层放第6、7、2、9卷，下层放第1、3、4、5、8卷，恰好得到了一个分数为1/2，罗德又用这九卷书重新排列：上层放第5、8、3、2卷，下层放第1、7、4、9、6卷；上层放第4、3、9、2卷，下层放第1、7、5、6、8卷；上层放第2、7、6、9卷，下层放第1、3、8、4、5卷；上层放第2、9、4、3卷，下层放第1、7、6、5、8卷；上层放第2、3、9、4卷，下层放第1、6、7、5、8卷；上层放第3、1、8、7卷，下层放第2、5、4、9、6卷；

当然这种答案不是唯一的，实际上我们利用数论中的同余法（或者利用弃九法）可以求出所有答案：

这道题实际上是一道生活中的排列组合问题，分为8个小问题，在这8个小问题中，答案的个数不唯一，最少有2个，最多可以达到46个，是训练孩子们思维的一道不可多得的耐人寻味的经典妙题。

面对如此多而巧的答案，在惊奇自然数如此之巧妙之外，我有丝忐忑，不禁想问，怎么约分啊？

或许是数字较大的问题，很多孩子没有化简，课堂教学时，学生们大声询问，算不算对，会扣几分，在应试教育的前提下，孩子们有这样的想法并不算错，但是对于我这位对数学有“洁癖”的人来说，就会感到有些不舒服，为什么我们不去追求的更完美一些，实际上这个分数很容易看出来公约数，能够较快地约分化为最简。

在人教A版必修3中有介绍国内外的两种求最大公约数的方法：辗转相除法和更相减损术。实际上求最大公约数的方法就是约分，将分子分母同时除以它们的最大公约数，就可以得到最简分数。（也可以求出两数的最小公倍数，利用两数之积等于它们的最大公约数与最小公倍数之积），今天，我们来谈谈我国的更相减损术。

“更相减损术”记载在公元1世纪前后、我国最重要的数学文献《九章算术》第一章“方田”中。《九章算术 方田》第六题：“有九十一分之四十九。问约之得几何？答曰：十三分之七。术日：可半者半之。不可半者，副置分母、子之数，以少减多，更相减损，求其等也。以等数约之”。这是《九章算术》对约分方法的完整总结。也就是说“更相减损术”的出现最初就是为了解决约分的问题。

课本上对更相减损术的解释：第一步，任意给定两个正整数，判断它们是否都是偶数。若是，用2约简；若不是，执行第二步。

第二步，以较大数减去较小的数，接着把所得的差与较小的数比较，并以大数减小数。继续这个操作，直到所得的数相等为止，则这个数（等数）或这个数与约简的数的乘积就是所求的最大公约数。

如：求120与144的最大公约数。

120÷2=60，144÷2=72

60÷2=30， 72÷2=36

30÷2=15， 36÷2=18

18-15=3

15-3=12

12-3=9

9-3=6

6-3=3

则3×2×2×2=24为120与144的最大公约数。

记得当初初次教学时就对这一方法进行研究，当时还讨论过为什么要有“可半者半之”这句话，半者之后最后还要乘上去，似乎有些麻烦，实际上我们在操作过程中完全可以把这句话舍去称为“副置分母、子之数，以少减多，更相减损，求其等也。”仍是求最大公约数的方法，我们不妨起个名字叫做“辗转相减法”，翻译成现代语言如下：任意给定两个正整数，以较大数减去较小的数，接着把所得的差与较小的数比较，并以大数减小数。继续这个操作，直到所得的数相等为止，则这个数（等数）就是所求的最大公约数。

譬如我们仍解决120与144的最大公约数。

144-120=24

120-24=96

96-24=72

72-24=48

48-24=24

则24为120与144的最大公约数。我们会发现这样做用到的减法次数和更相减损术是一样的，并且少了除以2和乘以2的步骤，那么为什么更相减损术要以2约之呢？当然有一个很有利的说服就是把大数变小，解决较小数的减法运算，难道仅仅是这个原因吗？当时我们学科教师也曾为这个问题争论，不急，我们慢慢道来。

先说这个所谓的辗转相减法最后得到的那个等数为什么就是两个正整数的最大公约数呢？

实际上这就是“初等数论”中的一些原理：

这种方法就变成“辗转相除法”，又叫做“欧几里得算法”。是公元前300年左右的希腊数学家欧几里得在他的著作《几何原本》中提出的。

也就是说，古希腊的“辗转相除法”是中国古代“辗转相减法(更相减损术)”的一个简洁表示的形式。它们在理论上是一致的，明显看出，“辗转相减法”和“辗转相除法”都是求最大公约数的方法。从计算上看，辗转相除法以除法为主；更相减损术以减法为主。计算次数上辗转相除法计算次数相对较少。特别当两个数字大小区别较大时计算次数的区别较明显。从结果体现形式来看：辗转相除法体现结果是以相除余数为0则得到。而更相减损术则以减数与差相等而得到。

实际上，更相减损术有着自己独特的优势，例如在求四个数1008，1260，882，1134的最大公约数，可以不拘次序地挑选最方便的，从较大的数减去较小的数，如果出现完全相同的余数，则这个余数就是所求的最大公约数。上诉四个数的最大公约数（1008，1260，882，1134）

=（1008-882，1260-1134，882，1134-882）=（126，126，882-6×126，252-126）=（126，126， 126，126）=126。

我们再回头看看，更相减损术的原文记载：术日：可半者半之，不可半者，副置子、母之

数，以少减多，更相减损，求其等也。以等数约之。——《九章算术·卷第一方田》

如何理解这个“可半者半之”。

我的理解是更相减损术的初衷是为了解决约分问题，而整数的奇偶性是可以一眼看出来的，所以首先约之，至于其他的约数不易判断，所以更相减损也就是说，不一定用2约之，其他的仍是成立的，譬如，求1850与13875的最大公约数：

但是这样的考虑，是解释了“可半者半之”，但是原文内还有“更相减损”，如何理解“更相”？

我的理解是：当两数中仅一数为偶数时，直接用2约简。这样，“更相减损”一句也豁然贯通了：“减”即指“以少减多”；“损”即指“可半者半之”；“更”即指“减、损”两操作交替进行(显然，这里“减”必然是两个奇数相减，其差必为偶数，因此每次“减”后必然有“损”的操作)。

接下来，我们用三种方法来解决《九章算术》中的问题：今有九十一分之四十九，问约之得几何？

辗转相除法：

91=49×1 42

49=42×1 7

42=7×6 0

则7为91与49的最大公约数。

更相减损术（课本记载），含辗转相减法：

91-49=42

49-42-7

42-7=35

35-7=28

28-7=21

21-7=14

14-7=7

则7为91与49的最大公约数。

修订后的更相减损术（体现更相）：

91-49=42（减），42÷2=21（损）

49-21=28（减），28÷2=14，14÷2=7（损）

21-7=14（减），14÷2=7（损）

则7为91与49的最大公约数。

从这一运算效果来看： “减”的主要目的是生成偶数，“损”才是减小数值的主要途径(这一点在数值较大的运算中尤为明显)。

说实话，小编更愿意相信：我国的智慧更超前、更领先、更先进。谈不上固步自封，但是我为我是中华儿女而骄傲！！！！！

,