距离空间（空间的距离）

空间的距离

中学教书时间长了，一拿到解析几何，似乎只能想起距离和角度，角度和距离……

今天先聊距离吧。

1、空间两个点的距离

无需多说，简单易懂。设点

，则

2、空间点到直线的距离

看起来很简单，其实特别特别麻烦，真的，不骗你。你要是不怕麻烦，我就举个例子一起算算。要是怕麻烦，请运动手指划过这一部分内容。

例、求点

到直线

的距离。

解法一、直接过点M作直线的垂线，垂足为P，则PM就是点M到直线的距离

面

的法向量为

面

的法向量为

所以，直线的方向向量为(3,3,2)。（此处略去草稿若干行）

所以，过点M且垂直于直线的面

的法向量为(3,3,2)

设平面

的方程为

代入点M(1,-1,0)得D=0

所以平面

的方程为

则直线与面

的交点P为

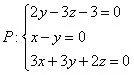
解得

（此处亦省略草稿若干行）

所以，点M到直线的距离为

解法二：点M到直线的距离=点M到直线上点的距离的最小值

由

得

设直线上的点为

则

当

时，

这个方法还算比较好啦，至少不会让我算得发疯。

解法三：设直线的方向向量为

，如果P为直线上的点，则距离

取直线

上的点P(0,0,-1)，已知M(1,-1,0)则

由解法一知直线的方向向量为

则

此法充分利用了向量，属于比较高档的解法了吧。

3、点到面的距离

前面已经写过一次推文，代公式即可

4、两平行线间的距离

很简单啦，直接化归成点到直线的距离即可。呵呵呵

5、异面直线间的距离

异面直线

和

间的距离，我们可以这样求。

过

上任一点作

的平行线

，

和

确定一个平面α

则异面直线

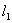
和

间的距离

=直线

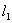
和平面α间的距离

=直线

上任一点和平面α间的距离

例、已知两直线

，求异面直线

和

间的距离。

解：由已知直线

的方向向量

直线

的方向向量

所以过

且与

平行的平面α的法向量为

取直线

上的点（0，0，-1），

上的点（1，1，1）则

平面α的方程为z-1=0

异面直线

和

间的距离

说起点到平面的距离，我想起高中学过的一个公式。

若点P为平面外一点，点Q为平面内一点，则点P到平面的距离

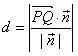
那么，我们也可以利用这个公式来改进本题的解法。

解法二：由已知直线

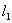
的方向向量

直线

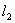
的方向向量

所以过

且与

平行的平面α的法向量为

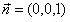
取直线

上的点P（0，0，-1），

上的点Q（1，1，1）则

异面直线

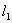
和

间的距离

表面上看只是省略了一个求面的方程的步骤，实际上是完全不同的思路。

练习：求异面直线

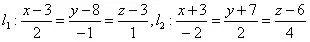
间的距离。

答案：

,