希尔算法的加密与解密（希尔密码的加密）

希尔密码是运用基本矩阵论原理的替换密码，由Lester S. Hill在1929年发明。

每个字母当作26进制数字：A=0, B=1, C=2... 一串字母当成n维向量，跟一个n×n的矩阵相乘，再将得出的结果模26。（注意用作加密的矩阵（即密匙）在 必须是可逆的，否则就不可能解码。只有矩阵的行列式和26互质，才是可逆的。）

用希尔密码对明文串 x = EastChinaNormalUniversity 进行加密，

密钥矩阵

加密：

密文向量 = 明文向量 * 密钥矩阵 (mod 26)

1. 先将明文串对应英文字母编码表进行数字转化 4 0 18 19 2 7 8 13 0 13 14 17 12 0 11 20 13 8 21 4 17 18 8 19 24

两两一组写成矩阵形式

我去，发现少了一个，老师出题就不能凑个整吗？？？ 这样子，我们做补0处理。

2. 接下来开始加密

得到密文矩阵后，按照分组对应的向量转成字母：

IK BX NB DH NN JD YE SR OB KB UJ HL W

python实现：

import numpy as np def encode(string, size): # 转换小写字母 if not string.islower(): string = string.lower() # 分成 size个 字的分段 blocks = [string[i:i size] for i in range(0, len(string), size)] # 明文字串与密钥矩阵阶数不整除。。字串补a if len(blocks[-1]) != size: blocks[-1] = blocks[-1].ljust(size,'a') # 将 a-z 编码为 0-25 temp = np.array([list(map(ord, block)) for block in blocks]) - ord('a') # print(temp) return temp def analysis(crypter, code): return ((crypter @ code.T) % 26).T ord('a') # 要加密的信息 encode_msg = 'eastchinanormaluniversity'.lower() print('待加密的信息：' encode_msg) # 密钥 encryption_matrix = np.array([[2, 5], [9, 5]]) print('密钥：') print(encryption_matrix) # 加密代码 encrypted_code = analysis(encryption_matrix, encode(encode_msg, 2)) # 密文 Decryption_matrixtext = ''.join(map(chr, encrypted_code.ravel())) print("密文：" Decryption_matrixtext[:len(encode_msg)].upper()) """ 待加密的信息：eastchinanormaluniversity 密钥： [[2 5] [9 5]] 密文：IKBXNBDHNNJDYESROBKBUJHLW """

解密:

不会求逆的参考:同余方程、欧拉函数、乘法逆元、定义在Zm上的矩阵求逆

解密和加密类似，先通过刚刚的方法计算出 模 m 的逆矩阵，然后用 A−1 再进行解密:

分析与破解

例子：

假设已知明文friday利用n=2的希尔密码加密，得到密文VYUZSM，求秘钥K.

n等于2，说明把friday分成3段，矩阵是2*2的

根据字母与整数的对应关系：

(5,17)---->(21,24),

(8,3)---->(20,25),

(0,24)—>(18,12),得到

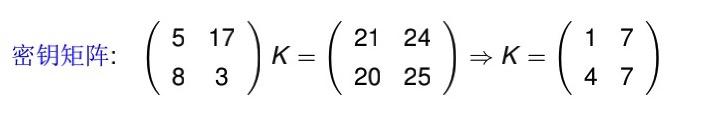
用(0,24)—>(18,12)验证K:

正确！得到密钥K就随便破解密文了