数学均值不等式证明（数学家柯西是如何证明算术-几何均值不等式的）

如果存在n个正数A,B,C,D,E……,那么就存在如下不等式

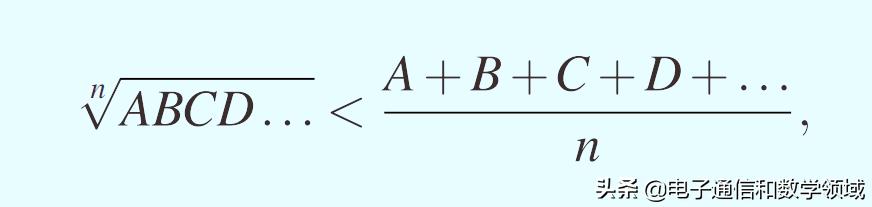
这就是著名的算术-几何不等式，又称作AG不等式，它在数学中非常重要，应用也很广泛，所以大家都应该很了解它

关于这个不等式的证明有很多，但最早给出严格证明的是大数学家柯西，柯西的证明至今仍被称作经典之作，下面就让我们来欣赏

首先N=2的情况，存在如下形式，一目了然

按照上述原理让我们依次让N=4，就会得到如形式

接着让N=8时的情况，

N=2^m时，就会得到如下非常巧妙的不等式

这里的N都是等比为2的几何级数：2,4,6,8,16,32………等等

在此假设如果n不是几何级数，最接近n的最小的数是2^m，且r=2^m-n，接着令

那么在n个正数A,B,C,D,E……和r个K的情况下，就会存在如下不等式，且等式右边等于K^2m

上述等式看上去比较困惑，但非常容易理解，数学技巧也非常巧妙

然后我们整理下这个不等式，就得到了著名的算术-几何不等式

例如：

上述的方法记载在柯西的名著《分析》一书中，证明技巧非常巧妙。