最大公约数培优（一只很励志的蚂蚁）

大家好！这节课的内容是一只闯荡几何世界的蚂蚁，经历太多思考追求，这次谈谈勾股定理的应用之空间最短路径问题。

在一个平面内，如果要从A点走到B点，怎么走路线最短呢？你一定会说，太简单了，"两点之间线段最短"嘛！的确如此，超级课堂在之前的视频中也着重强调过这一点。在一个平面内，A点到B点的最短路径就是线段AB。不过我们还会经常遇到另外一种情况，当运动路线不是平面，而是某个几何体的外表面的情况。这种题目被称为"空间最短路径问题"，而且都会涉及一只蚂蚁，这只蚂蚁特别的辛苦，一直闯荡于几何世界，按出题老师的意图从一个点爬到另一个点，甚至爬N圈，永不停歇。这节课就带你具体研究一下这类题目的解法。

我们先来看一个最简单的例题：

如图，边长为1的正方体中，蚂蚁君从A顶点出发沿着正方体的外表面爬到B顶点的最短路程是 ．

我蚂蚁君不是超人，不能从立方体中间"穿过"，只能沿着立方体外表面运动。对于"空间距离问题"，千年不变的解题思想就是：把空间问题转化为平面问题，万年不变的具体操作就是将几何体外表面展开。我们把正方体展开，画出AB点的位置，连接AB。你会发现类似这样的路线一共有6条，我们把正方体的六个面称为上下左右前后，这六条路线的爬行顺序依次是"前上"、"前右"、"左上"、"左后"、"下右"或"下后"。但这六条路线的长度都是一样的，展开后，都是这么一个矩形的对角线。利用勾股定理，求得长度为√5，所以蚂蚁从A到B爬行的最短距离是√5。

路途坎坷，经历不都是方方正正，苦逼蚂蚁君又经历如下历程的磨难：

1．（2018秋•锦江区期中）边长分别为4cm，3cm两正方体如图放置，点P在E₁F₁上，且E₁P＝1/3E₁F₁，苦逼蚂蚁君如果要沿着长方体的表面从点A爬到点P，需要爬行的最短距离是____ cm．

求出两种展开图PA的值，比较即可判断,如图，有两种展开方法：

2.如图所示，一棱长为3cm的正方体，把所有的面均分成3×3个小正方形，其边长都为1cm，假设苦逼蚂蚁君从下底面点A沿表面爬行至侧面的B点，最少要爬______ cm．

把此正方体的点A所在的面展开，然后在平面内，利用勾股定理求点A和B点间的线段长，即可得到蚂蚁爬行的最短距离．在直角三角形中，一条直角边长等于5，另一条直角边长等于2，利用勾股定理可求得．

因为爬行路径不唯一，故分情况分别计算，进行大、小比较，再从各个路线中确定最短的路线．

所以最短路径长为5cm，故答案为：5.

除了正方体的表面距离问题，圆柱体的表面距离问题也是很常见的. 比如：

3. 如图，一圆柱高8cm，底面半径为6/πcm，又是苦逼蚂蚁君从点A爬到点B处吃食，要爬行的最短路程是多少？

同样的方法，将圆柱体外表面展开是一个长方形。它的宽是圆柱体的高8cm。长是底面圆的周长12cm。沿圆柱表面运动就相当于沿这个长方形表面运动，连接AB，就是我们要求的长度。而右上角的B点恰好是边的中点，AD＝6cm，BD＝8cm，在Rt△ADB通过勾股定理就能马上算出最短距离AD=10 cm.

4．（2018秋•宝安区期中）如图，已知圆柱的底面周长为6，高AB＝3，苦逼蚂蚁君在圆柱表面爬行，从C点爬到对面的A点，然后再沿另一面爬回C点，则苦逼蚂蚁君爬行的最短路程为 _______．

把圆柱侧面展开，展开图如右图所示，点A、C的最短距离为线段AC的长．在RT△ADC中，∠ADC＝90°，CD＝AB＝3，AD为底面半圆弧长，AD＝3,所以AC＝3√2，∴从C点爬到A点，然后再沿另一面爬回C点，则小虫爬行的最短路程为2AC＝6√2，

5. （2018秋•金牛区校级期中） 如图，圆柱形容器高为6cm，底面周长为6cm，在杯内壁离杯底2cm的点B处有一滴蜂蜜，此时苦逼蚂蚁君正好在杯外壁，在甜蜜回忆基础上，离杯上沿2cm与蜂蜜相对的点A处，苦逼蚂蚁君很想从外壁A处到达内壁B处的以最短距离达到，则最短距离为 ______．

将杯子侧面展开，建立A关于EF的对称点A′，根据两点之间线段最短可知A′B的长度即为所求．将杯子侧面展开，作A关于EF的对称点A′，连接A′B，则A′B即为最短距离，

总结一下，求空间最短路径长度的解决步骤：第一步确定最短路径，方法是将运动所经过的外表面展开，最短路径就是在展开平面内两点间的线段；第二步求线段长度，方法是利用勾股定理求斜边。

刚才我们说过了立方体表面的最短路径问题，它的六种路线是完全一样的。下面我们把立方体换成棱长不等的长方体，这时情况会变得稍稍复杂一些，比如这道题：

6.如图，地上放着一个长、宽、高分别为50cm、40cm、30cm的箱子，位于角A处的苦逼蚂蚁君发现了位于角B处的一只苍蝇，问苦逼蚂蚁君沿着箱面怎样爬才能使它到B处的路程最短，最短路程是多少？

与立方体一样，苦逼蚂蚁君同样有六种路线："前上"、"前右"、"左上"、"左后"、"下右"或"下后"，每种选择都要经过两个长方形。但题目并没有指定选 择哪种路线，而长、宽、高又各不相等，所以这六种路线的长度就不再相等了。由于长方体相对的面全等，于是我们可以把这六种路线分成三类："前上"与"下后"一类， "前右"与"左后"一类，"左上"与"下右"一类， 比较这三类的结果，这种选择的路程最短，

7．（2018秋•新吴区校级期中）在一个长为8分米，宽为5分米，高为7分米的长方体上，截去一个长为6分米，宽为5分米，深为2分米的长方体后，得到一个如图所示的几何体．苦逼蚂蚁君要从该几何体的顶点A处，沿着几何体的表面到几何体上和A相对的顶点B处吃食物，那么它需要爬行的最短路径的长是 _____分米．

根据题意把图形的侧面展开，如图所示，利用勾股定理求解即可．

以上几个例子，在表面走的距离都不够长，如果在绕表面运动不止一圈的话又会是什么情况呢？蚂蚁君已经被玩坏了，让它休息一下，这次我们在几何体表面缠绕细线。

8.如图，长方体的底面边长分别为1cm和3cm，高为6cm．如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B，那么所用细线最短需要______ cm；如果从点A开始经过4个侧面缠绕n圈到达点B，那么所用细线最短需要______ cm．

仔细想想，这根细线的总长度其实就是A和B的空间最短路径长度。所以我们依然要把长方体的侧面展开。由于题目已经指定了路线选择：前右后左，所以展开图中长方形的形状就是固定的。这是绕了一圈的情况，那么绕了n圈的展开图该怎么画呢？我们可以找找规律：如果只绕1圈，展开图就是4个长方形，一边长就是3 1 3 1，8cm；如果绕2圈，那么会经历两次"前右后左"的过程，所以展开图就是8个长方形，一边长就是16cm……绕n圈就是经历n次"前右后左"的过程，展开图就是4n个长方形，一边长就是8ncm。就像图中这样的一个很长很长的长方形。

将长方体展开，连接A、B，根据两点之间线段最短，

有了前面的基础，我们最后再来解决一个平面与空间结合的最短路径问题，让蚂蚁君继续上场：

9.（2018秋•三明期末）如图，ABCD是长方形地面，长AB＝10m，宽AD＝5m，中间竖有一堵砖墙高MN＝1m．蚂蚁君从点A爬到点C，它必须翻过中间那堵墙，则它至少要走_____ m．

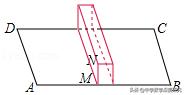
我们可以把这个木条看成矩形场地凸起的一段。蚂蚁会经过长方体的三个侧面，我们便把这三个侧面展开，相当于矩形场地ABCD的长AB被"拉伸"了一部分，拉伸的长度就是三个侧面长方形的宽。

连接AC，利用勾股定理求出AC的长，再把中间的墙平面展开，使原来的矩形长度增加而宽度不变，求出新矩形的对角线长即可．

如图所示，将图展开，图形长度增加2MN，

原图长度增加2米，则AB＝10 2＝12m，

连接AC，∵四边形ABCD是长方形，AB＝12m，宽AD＝5m，

∴蚂蚱从A点爬到C点，它至少要走13m的路程．

故答案为：13．

10.如图是一个三级台阶，它的每一级的长、宽、高分别为5dm，3dm，和1dm，蚂蚁君想尝试上台阶寻找美味，想从点A，想到点B去吃食物，请你计算，这只蚂蚁从点A爬到点B走得最短路程是多少？

有了上面经验，将台阶展开得到的是一个矩形，蚂蚁君要从B点到A点的最短距离，便是矩形的对角线，利用勾股定理即可解出答案．

将台阶展开，如图，因为AC＝3×3 1×3＝12，BC＝5，所以AB²＝AC² BC²＝169，所以AB＝13（dm），所以蚂蚁爬行的最短线路为13dm．

你看，只要你清楚空间最短路径问题的解决方法，遇到这种看似复杂的平面、空间混合问题也可以轻松搞定了。无论题型怎么变化，你只要记住把几何体表面展开，化空间为平面就能秒杀任何题目了。

这节课就讲到这里，我们来总结一下，主要研究了空间最短路径的解决思想：把空间问题转化为平面问题，具体操作就是将几何体外表面展开。求最短路径的方法是利用勾股定理求斜边。

在题目中要注意以下三点：

1、遇到长方体表面的最短路径问题时，如果题目没有指定路线的选择，要注意分类讨论；

2、如果沿几何体表面运动n圈，相当于经历n次循环，展开图中的长要扩大为n倍；

3、平面、空间的混合问题只需要把经历的几何体表面展开，与平面连接在一起便可以轻松解决。

立体图形的蚂蚁爬行问题，这课堂已经把考试会遇到的几种情况都讲解完毕了。以后你再遇到这种题目，就能完全理解蚂蚁的心思，迅速找到解题的方法，爬到胜利的终点！

,