图形平移的关键要素是平移的什么和什么（掌握图形平移2个核心要素）

（2）在评论区留言支持！

（3）把这份资料转发给需要它的同学！

（4）你自己（亲友）能收藏用上这份资料！

（5）在本文之前和之后，已发布大量的相关复习资料，欢迎查阅使用。

​一、选择题

1. C；2. C；

3. 考点关于x轴、y轴对称的点的坐标；坐标与图形变化-平移．分析根据题意可以求得点A′的坐标，从而可以求得点A′关于y轴对称的点的坐标，本题得以解决．点评本题考查关于x轴、y轴对称的点的坐标、坐标与图形的变化﹣平移，解题的关键是明确题意，找出所求点需要的条件．

4. 考点坐标与图形变化-平移．分析直接利用平移中点的变化规律求解即可．点评本题考查了坐标系中点、线段的平移规律，在平面直角坐标系中，图形的平移与图形上某点的平移相同．平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．

5. 答案B。解析图①中的点A和图②中的点A′是一对对应点，将点A先向右平移1个单位，再向下平移3个单位就得到点A′，所以B选项正确．故答案选B．

6. 考点坐标与图形变化-平移．分析根据点A、B平移后横纵坐标的变化可得线段AB向左平移2个单位，向上平移了3个单位，然后再确定a、b的值，进而可得答案．

7. 分析直接利用平移的性质结合轴对称图形的性质得出答案．

二、填空题

9. 如图，△ABC中，BC=5cm，将△ABC沿BC方向平移至△A′B′C′的对应位置时，A′B′恰好经过AC的中点O，则△ABC平移的距离为　2.5　cm．考点平移的性质．分析根据平移的性质：对应线段平行，以及三角形中位线定理可得B′是BC的中点，求出BB′即为所求．

11. 考点翻折变换（折叠问题）；等边三角形的性质；坐标与图形变化-平移．分析据轴对称判断出点A变换后在x轴上方，然后求出点A纵坐标，再根据平移的距离求出点A变换后的横坐标，最后写出即可．

12. 分析直接利用平移的性质得出EF=DC=4cm，进而得出BE=EF=4cm，进而求出答案．点评此题主要考查了平移的性质，根据题意得出BE的长是解题关键．

13. 考点平移的性质．分析直接利用平移的性质得出顶点C平移的距离．解答解：∵把三角板的斜边紧靠直尺平移，一个顶点从刻度“5”平移到刻度“10”，∴三角板向右平移了5个单位，∴顶点C平移的距离CC′=5．故答案为：5．　

三、画(作)图题

19.分析（1）直接利用平移的性质得出，点位置，进而得出答案；（2）直接利用菱形的判定方法进而得出答案．点评此题主要考查了菱形的判定以及平移变换，正确掌握菱形的判定方法是解题关键．

四、应用题

22. 分析：（1）直接利用平移的性质得出平移后对应点位置进而得出答案；（2）利用轴对称图形的性质得出对应点位置进而得出答案．点评：此题主要考查了轴对称变换以及平移变换，根据图形的性质得出对应点位置是解题关键．

23. 分析：（1）根据题意画出即可；关于y轴对称点的坐标纵坐标不变，横坐标互为相反数；（2）根据网格结构找出点A、B、C以点O为旋转中心顺时针旋转90°后的对应点，然后顺次连接即可；（3）利用△ABC旋转时BC线段扫过的面积S扇形BOB2﹣S扇形COC2即可求出．点评： 本题考查了利用旋转变换作图，轴对称和扇形面积公式等知识，熟练掌握网格结构准确找出对应点的位置是解题的关键．

24. 分析：（1）根据图形平移的性质画出△A1B1C1；（2）根据旋转的性质画出△A2B1C2；（3）利用扇形面积公式求出即可．点评：此题主要考查了扇形面积公式以及图形的平移、旋转变换等知识，熟练掌握扇形面积公式是解题关键．　

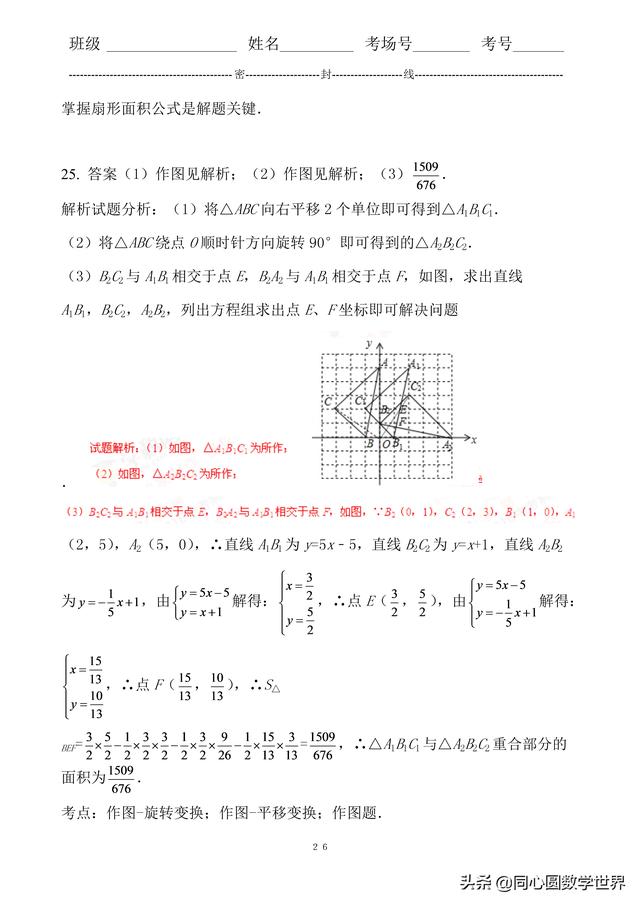
25. 答案（1）作图见解析；（2）作图见解析；解析试题分析：（1）将△ABC向右平移2个单位即可得到△A1B1C1．（2）将△ABC绕点O顺时针方向旋转90°即可得到的△A2B2C2．（3）B2C2与A1B1相交于点E，B2A2与A1B1相交于点F，如图，求出直线A1B1，B2C2，A2B2，列出方程组求出点E、F坐标即可解决问题。考点：作图-旋转变换；作图-平移变换；作图题．

26. 考点作图-旋转变换；作图-平移变换．分析（1）由B点坐标和B1的坐标得到△ABC向右平移5个单位，再向上平移1个单位得到△A1B1C1，则根据点平移的规律写出A1和C1的坐标，然后描点即可得到△A1B1C1；（2）利用网格特点和旋转的性质画出点A1的对应点为点A2，点B1的对应点为点B2，点C1的对应点为点C2，从而得到△A2B2C2；（3）先利用勾股定理计算平移的距离，再计算以OA1为半径，圆心角为90°的弧长，然后把它们相加即可得到这两次变换过程中，点A经过点A1到达A2的路径总长．

27. 考点位似变换．分析根据点B的坐标和点D的坐标，求出OB=4，OD=6，得出=，再根据△OAB与△OCD关于点O位似，从而求出△OAB与△OCD的相似比．

29. 考点作图-旋转变换；作图-平移变换．分析①根据△ABC沿BA方向平移，在网格中画出当点A移动到点A1时的△A1B1C1即可；②画出△A1B1C1绕点A1按逆时针方向旋转90°后得到△A2B2C2，求出点B1旋转到B2的路径长即可．

30. 分析（1）由旋转的性质得，AD=AB=10，∠ABD=45°，再由平移的性质即可得出结论；（2）先判断出∠ADE=∠ACB，进而得出△ADE∽△ACB，得出比例式求出AE，即可得出结论．