动量守恒定律的难点题型（动量守恒中的共速问题）

在动量守恒中，经常存在共速问题，可以用数学证明，

共速时，动能损失最大，反之亦然，类比于完全非弹性碰撞，下面分情况来分析。

1.系统内存在滑动摩擦力

例题：如图所示，

质量为M的小车置于光滑的水平面上，车的上表面是粗糙的，有一质量为m的木块，以水平初速度v₀滑上小车的水平上表面.若车的上表面足够长，则(B)

A.木块的最终速度为零

B.木块的最终速度一定为mv₀

/(M＋m)

C.由于车的上表面粗糙，小车和木块组成的系统动量减小

D.车的上表面越粗糙，木块减少的动量越多

由于系统内只存在滑动摩擦力，滑动摩擦力的效果是阻碍相对运动，最终达到共速，又系统动量守恒，B选项是正确的。

由于滑动摩擦力的存在，就会摩擦生热，从而动能转化为内能，转化的内能为mv₀²/2-M(mv₀/(M＋m))²/2，与动摩擦因数μ无关，μ只是影响了相对滑动的位移。

例题：如图所示，

在光滑水平面上一质量为m的物块以初速度v₀与质量为M的物块发生碰撞后粘在一起，则在两物块碰撞过程中产生的焦耳热Q为多少？

分析：两物块发生碰撞后“粘在一起”，即碰撞后一共同速度运

动，动能转化为内能，典型的“共速模型”。这类问题属于完全非弹性碰撞，其处理方法大都是采用动量和能量的观点加以分析。

2.系统内存在弹簧

例题：如图所示，

两滑块A、B位于光滑水平面上，已知A的质量MA＝1kg，B的质量MB＝4kg.滑块B的左端连有轻质弹簧，弹簧开始处于自由伸长状态.现使滑块A以v＝5m/s速度水平向右运动，通过弹簧与静止的滑块B相互作用（整个过程弹簧没有超过弹性限度），直至分开，则(D)

A.物块A的加速度一直在减小，物块B的加速度一直在增大

B.作用过程中弹簧的最大弹性势能Ep＝2J

C.滑块A的最小动能为EkA＝4.5J，滑块B的最大动能为EkB＝8J

D.若滑块A的质量MA′＝4kg，B的质量MB′＝1kg，滑块A的最小动能为EkA′＝18J，滑块B的最大动能为EkB′＝32J

把A、B、弹簧看作系统，系统动量守恒，机械能守恒。

弹簧弹性势能最大，即A、B动能损失最大，也就是A、B共速时，动能转化为弹性势能。

3.最大高度

例题：如图所示，

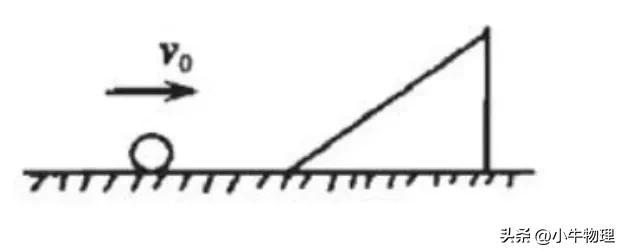
在光滑水平面上静止一质量为M的光滑斜面，一质量也为M的小球以初速度v₀冲上斜面，斜面足够长，在小球与斜面作用的过程中，下列说法正确的是（）

A.小球到斜面最高点时小球速度为0

B.小球到斜面最高点时斜面速度大小为v₀/2

C.小球返回斜面底端时，小球的速度大小为v₀

D.小球返回斜面底端时，小球的速度为0

动能转化为重力势能。

例题：如图所示，

质量为M的小车A置于水平光滑的轨道上，其下端通过质量可忽略的绳将质量为m的货物B悬挂在空中，系统处于静止状态。若突然给A一水平向右的初速度v₀，求货物B能摆起的最大高度。

动能转化为重力势能。

4.子弹打木块

例题：质量为2kg的小平板车B静止在光滑水平面上，板的一端静止着一物体A，mA＝2kg，如图所示。一颗质量为20g的子弹，以600m/s的水平速度射穿A后，速度变为100m/s。假设A、B间的动摩擦因数为0.05，子弹穿过A的时间极短，g取10m/s²。

（1）子弹射穿A时，A的速度为多大？

（2）当A与B相对静止时，它们的共同速度为多大？

动能转化为内能。

通过以上几种情况的分析讨论可以看出，题目中如果出现了诸如“粘在一起”、“未穿出”、“最长”、“最短”、“最远”、“最近”、“最高”等关键词，其所处的状态通常都是在共速之时。反过来，如果题目中需要求解当其达到共速的情景，则需分析是否存在“粘在一起”、“未穿出”、“最长”、“最短”、“最远”、“最近”、“最高”等关键词。分析出相应的状态，将其归纳为“共速模型”，用“共速模型”的分析方法基本上就成了一种固定的模式。

,