学习数学分析对高等数学有帮助吗（数学并不只有计算）

点击右下角“关注”我噢

作者|川妈&超儿

有句话说的“真好”，直戳老母亲的内心：

“如果说英语是老母亲心里的白月光，那数学真可谓是现实中的蚊子血，躲不开又逃不掉。”

奥数、珠心算、速算.....这些特别项目孩子当然可以选择不学，但从小学到大学的基础数学是怎么也躲不开的。而对我这样以数理见长的老母亲来说，对孩子学好数学又有着别样的“迷思”。

所以，一直苦心钻研各种学习方法和资源。但即使这样，我在小川的数学启蒙上还是犯了错误

。

估计是先前经验的惯性影响，我还是会不由自主地更加重视训练他的“计算能力”。在一段时间里，他很快就熟练掌握了100以内加减法和乘除法。

却在我认为很简单的地方，翻了跟头。之前，他对由小方块堆砌起来的立体图形，常常数不清隐含在背后的块数、辨不清立体图的三视图。

遇到问题就得解决，查了很多资料之后，我才明白自己把数学想简单了，孩子想学好数学，需要的是多元能力。

低年级的算术，和高年级的平面几何、立体几何等高阶段的数学，需要具备的能力根本不一样！

算术要求的是语言能力，而平面、立体几何等依靠的视觉-空间能力，关键两者还互不相关！

在数学教育王者之一的新加坡，数学的技能训练（俗称刷题）被排到了最后；而以培养孩子视觉-空间能力为重点的Visual Math（视觉数学）被放在了关键位置。

它不但是孩子进行高阶数学学习的基础，也是前期数学启蒙的重要方式。

1什么是视觉数学

斯坦福大学的科学家对大脑进行扫描时发现，当人在处理数学问题时，大脑有5个部分在工作，其中有两个部分跟视觉有关（绿色 橙色部分），而不仅仅是对抽象数字的理解、记忆和执行。

视觉数学，顾名思义，就是利用一些具象化的东西，或画图，或教具来呈现数学里的抽象概念，进而学习数学的方法。这是当今非常流行的数学教学方式，在新加坡和美国数学里，都已经有大量的应用。

视觉数学包括两大块内容，分别对应大脑的两个区域，一个负责空间想象和数量统计（比如图一），一个是负责处理图象符号（比如图二）。

图一、需要孩子大脑计算出那些肉眼可见的、以及不可见的方块，然后才能计算数量，可通过教具进行展示。

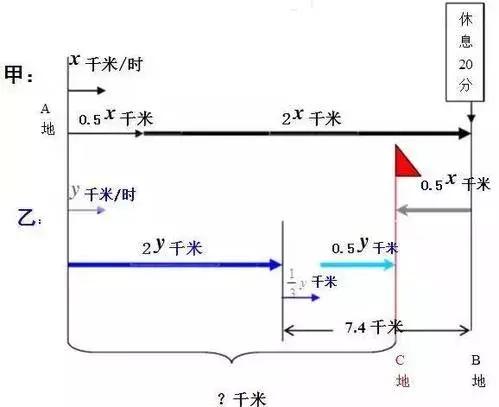
图二、数学当中的行程问题，用图示方式展现。

其实，这些具象思维能力，孩子天生就有。没有学过加法的孩子，也能说出1个苹果 1个苹果等于2个苹果。

只不过，数学毕竟是一个抽象概念和思维的集合。我们在教孩子数学时，往往忽略了这项基础能力，而过多去追求更加抽象的计算能力。

在走了弯路之后，我开始反思自己教孩子数学的策略和方法，在依然重视锻炼孩子计算能力的同时，着力培育他的视觉-空间能力。

具体怎么做？一种方法，之前就推荐过，新加坡数学（我们的数学教学中也有，只不过他们似乎强调的更多些）倡导的建模方法。

另一种方法，早在教育学家蒙台梭利时代，就被倡议和广泛采用过的——数学教具法。

教具独特的特性（科学性、针对性、可视性、完整性），特别是能够有针对性地帮助孩子理解所讲内容，一直以来在教学中发挥着重要的作用。

蒙台梭利的经典教具固然好，我又找到了一些更加有趣的新版本。为了提高针对性，我还特意买了一整套小学数学课本和义务教育阶段的数学课程标准，根据知识特点和课标要求，又在其中进行了筛选，最终选择了这几个先推荐给大家。

2LR MathLink Cubes

适用年龄：3岁

对应知识点和数学能力：

初级：认识数字、建立数量关系（分类、归纳、逻辑推理、手眼协调）；

中级：比大小、加减法、写个数、测量；

高级：乘除、周长、面积、几何图形拼接及观察三视图（几何空间思维、逻辑推理）。

特点：循序渐进的题卡。

玩法：（因为太多了，举例说明）

1.数的理解

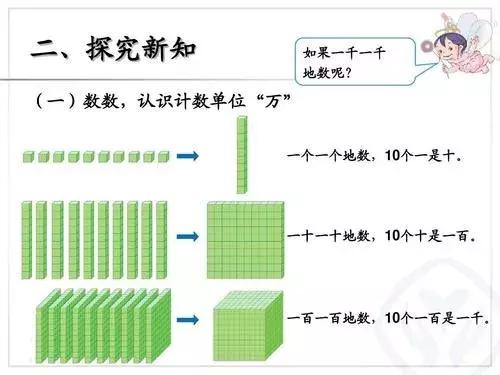
小学课标要求理解万以内数的意义，从十，然后过渡到百、然后到千、万这种大数。

实际教学中，也常常利用图片或教具进行教学。

这套教具里的积木和题卡的结合，能让孩子更加容易地理解大数概念。

2. 运算卡

一年级这样的习题，随处可见。

运算卡的本质其实就是新加坡数学的建模方法，一方面将抽象的数学计算转化为孩子可以看得见的画图模型，更形象、更容易理解；另一方面，又将实物加减转化为有一定抽象程度的数学模型，帮助孩子实现从具象向抽象的转变。

3.图形与几何

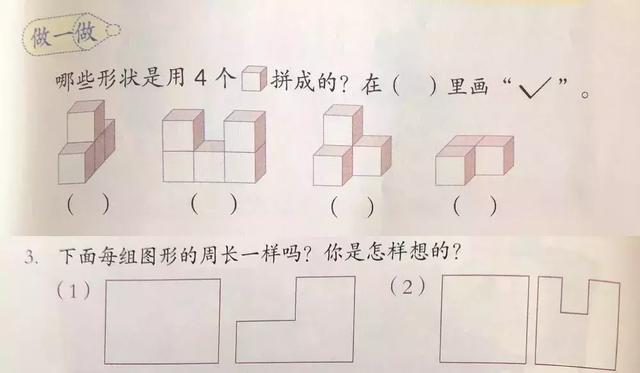
“题卡 积木”还可以帮助孩子掌握统计小立方块的数量、面积、周长的方法。

小川之前在进行立体方块统计的时候，就常常用这套教具来帮他建立空间图形，加深理解。

4.逻辑推理、归纳

类似这种归纳推理题，小学一年级频繁出现。

也可以利用这套教具来从小培养。

点评：

这是一套类似乐高积木的教具，囊括了从基本识数到计算、立体、逻辑推理等等广泛的学习内容。最大的有优点就是配有拾级而上的题卡，我们可以根据题卡的顺序，循序渐进地引导孩子进行数学启蒙、更高阶段的学习。

3Saalin TANGRAM七巧板

无论国内国外，从来都不缺七巧板的身影，因为它对孩子逻辑推理、几何图形的理解，实在太重要了！

国内直接把七巧板放在了小学一年级的教材里，甚至在幼升小的题目中，就有七巧板的身影。

适用年龄：一套为3岁 （彩色，各种形状和生活用品）；两套为5岁 （同种颜色的动物 彩色人物）。

对应的知识点和数学能力：

数学知识：数数、大小、图形（基本：三角形、正方形、平行四边形）、角、面积、对称、旋转、平移、全等；

数学能力：几何、空间思维、逻辑推理、专注力。

特点：

1.设置关卡，循序渐进。

3岁 和5岁 ，三套教具，每套2个难度的level。

从1块的形状到7块的形状拼接和生活用品、动物拼接。

每张题卡的背后都有拼接答案。

颜色从七色过渡到单色，难度升级。

2.学习视频。每个level都对应了教学视频，方便孩子观看、学习。

3.易携带。合上是一本书，打开，左边是题卡，右边是操作版。之前小川出去吃饭的时候，常常间歇就拿出来玩。

4.不易移位。形状保持完整。

玩法：

1.对称 旋转 平移

对于这几个知识点，1~3年级课标都有了具体的要求和实例。

看似简单的7个基本图形，通过看似也不难的平移、旋转，却能变化出数不清的图形，考察的不仅是孩子的图形布局能力，还有逻辑推理能力等等。

我陪小川玩的过程，愈加发现其中的变化多端和深不可测，当然也有妙不可言的成就感和满足感。

2.面积 全等

7~9年级的课标中，明确规定了全等三角形的要求：理解全等三角形的概念，能识别全等三角形中的对应边、对应角。

点评：

在每个孩子的数学几何启蒙中，七巧板是不可或缺的一个教具。这套七巧板，几乎完美吸纳了所有七巧板的优点。在家长的引导下，每个孩子，都可以玩出自己的新花样。

4Geomakers Dive into Shapes

这是一套STEM教具，更是一套妥妥的立体几何教具，对孩子空间想象能力和初步进入几何知识的学习，帮助不小。

适用年龄：5岁 （我认为可以适当低龄，3岁 ，孩子可以进行大小的比较，面积大小的比较、周长的比较）

对应的知识点和数学能力：

数学知识：面积大小、立体几何知识、体积的概念；

数学能力：立体空间想象力、专注力、手眼协调。

特点：给我足够的点和线，我就能拼出各种形状的几何体。

1.有长短不一的直线，也有曲线。能拼接不同的立方体。

2.两种不同的球，球上有不同的孔数量，可满足不同的接点。

3.颜色丰富，符合孩子的审美特点。

玩儿法：基础玩法 创造玩法。

基础玩法：孩子可以根据游戏卡的题目，拼搭出不同形状的立方体。前期如果经过七巧板的平面图形拼搭的训练，对孩子转化立体图形拼搭会有很大的帮助。

创造玩法：

首先，对于低龄的小孩子，可以根据平面图形的拼接，了解面积和周长的的概念，并比较其大小。

大正方形套着小正方形，周长和面积，都是外面的大正方形大。

对于大龄的孩子，除了立体的拼搭之外，还可以开拓孩子的想象力，发掘出其他特殊形状的拼接。

点评：

这款不同于封闭的立方块，它的框架性的结构对以后孩子学习立体几何辅助线的添加，会有很大的帮助。

5Base Ten STARTER SET

这套教具，可以说是一套完整的美国数学教辅——立方块 习题集。

适用年龄：6岁 （立方块）；3~6年级（习题集），我认为这套教具年龄可以下降到3岁 ，习题集可以5岁 。

对应的知识点和能力：

数学知识：算术、位数的理解、分数、倍数、面积、体积；

数学能力：几何、空间思维、手眼协调。

特点：

1.跟中国的数学课标要求基本类似。

美国3-6年级教材可以顺延至中国的1-3年级。

2.立方块 习题集。非常适合学前班和小学阶段的系统性数学学习。

玩儿法：不带习题集（低龄） 带习题集（学前班 学龄段）

不带习题集玩法：里面有不同的方块，可以比较大小（顺带可以加上 >、<符号的理解），也可以归类、数数。

带习题集玩法：按照习题集要求的知识点，在教具中具体实现。

1.大数、位数概念的学习

与上文中LR MathLink Cubes类似，就不多赘述了。但是教材中的一个关于大数习题，还是很有意思的（家长可以参照这样的方法，引导孩子学习）。

2.分数（如1/10~1，1/100~1等） 周长 面积

在小学1~3年级的数学课标对分数、周长、面积做了明确要求。

我们可以用这套教具，结合教材，引导孩子理解分数的概念，以及分数的计算。

点评：

亮点是习题集，全英文，但比较容易理解（一边做题，一边还可以学英文）。一些习题设计的非常有意思，比如学习计算以及个十百千时，就会通过拼凑一个动物展开。

6PRof.MaRbles

这是一款培养孩子逻辑推理和空间思维非常有意思的教具，但同时也是一个很多低龄孩子喜欢玩的玩具。

同事家的两岁宝宝，玩的不亦乐乎，同时还在数着1、2、3、4......

适用年龄：官方建议7-99（但是我个人觉得可以放低年龄到2岁 ）

对应知识点和能力：

数学知识：数数、建立数字和图形的关系、比较大小、算术、数学排列组合的最短路径问题

数学能力：逻辑推理、空间思维、专注力、规则意识

特点：

1.有游戏规则，孩子通过游戏规则找到最短路径。

在培养孩子一些数学思维能力的同时，也可以培养孩子的规则意识，理解社会上也是有规则存在的。

2.配备题卡，难度循序渐进。

玩儿法：基础玩法（低龄） 规则玩法（7岁以上）

基础玩法：

1.低龄孩子可以进行数数，建立数字抽象和球一一对应关系等，来培养基本的数感。

瓶身上标准了数字，所以引导孩子进行数概念理解的时候，这样更加方便对数字的理解，以及利用高矮，球的多少来建立数字大小的关系。

同事家竟然将其玩成了“弹溜溜球”，孩子也是玩得超级开心。

规则玩法：

1.题卡，共有60道题，前面为题，背面为答案。

2.题目中，箭头前方为原始状态，箭头后为瓶的最终状态。

3.具体规则：

（1）每次倾倒球，两个条件必须满足其一：输出瓶里的球全部倒出或者接收瓶装满；

（2）最短路径，即所需要的步数最少（圆盘为步数计步器）。

视频中详细介绍了最短路径的选择，在选择过程中要经过试错、逻辑推理等能力。

在平常的考试中，最短路径问题非常常见。比如小学三年级奥数和初高中的排列组合问题。

点评：

这是一套适合训练孩子排列组合、逻辑推理能力的教具，从2步路线一直升级到18步路线，难度逐渐升级。

7BLOCK BY BLOCK（堆砌大师）

这是Thinkfun一款非常经典的教具，可以说是立体版的七巧板，利用7块不同的立方积木，组合成N种不同造型。

小川对此特别痴迷，刚拿到的时候，常常一个人玩好久，太烧脑了！我和川爸，也常常陪他一起，燃探寻立体几何的奥秘。不过刚开始的时候，用了10分钟，也才过了2关。

适用年龄：官方建议8岁 ，实际4岁 就可以玩（用少量的、简单的积木拼搭）。

对应知识点和能力：

数学知识：三维图向二维图转化、理解三视图、统计

数学能力：逻辑推理、空间思维、专注力、分析问题的能力

特点：

1.两种不同类型的积木——平面型和立体型。这种设计满足了立体空间搭建的基础，也满足了低龄孩子单纯用平面型来搭建。

平面型分4种：T型、L型、Z型，可以展示一个平面或者转角；

立体型有3个：转化成各种转角。

2.易携带、棱角圆润。7个积木放在自带的收纳袋里，可以随时带着玩，旅途就是非常好的时机。

玩法：简易玩法 高级玩法

简易玩法：

（1）通过不同立体积木，可以在前期让孩子先玩平面型积木。

用平面型积木堆起来的床

（2）在题卡的答案中，分为Hint1（4块积木提示）和Hint2（3块积木）

4~6~8岁可以根据7块积木的提示来进行搭建，或者只是根据Hint1或Hint2的部分提示进行搭建。这个搭建的过程，也是空间思维搭建的过程；

8岁 ，独立拼接。

当然孩子第一次接触的时候，因为难度比较大，也可以根据这样的顺序，循序渐进地进行。

高级玩法：

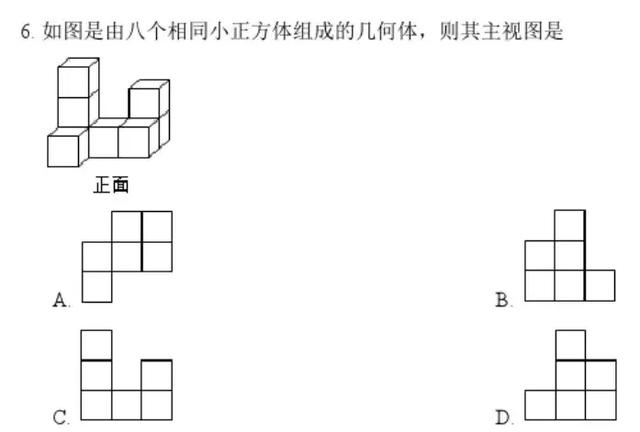
1.视觉数学的第一个板块——空间想象、数量统计，其对应的常见考题就是三视图和统计小方块。

三视图

统计方块个数

在这套教具中，随时可以进行上述练习，并画出二维图，加深理解。

2.根据题卡进行训练——空间 推理的实战练习。

试错 推理 返工，是常常要做的。

点评：

这套教具的烧脑，可以说非常明显，但是它对孩子专注度的训练非常好。小川玩它时的专注度和挑战精神，让我有些感动。

8Geometric Solids

这是一套带领孩子认知立体形状和学习体积计算的绝佳教具。

适用年龄：8岁 ，可以放宽年龄至4岁 ，学前班就已经开始进行立体形状的认知了。

对应知识点和能力：

数学知识：几何体的形状认知、面积关系和计算，三位图形向二维图的转化、三视图

数学能力：空间想象、计算能力、推理

特点：

1.每个几何体均在包装盒背面写明了边长长度，用于体积计算。

2.每个几何体均为敞口、透明设计，可以通过注水、装沙、做软陶模型来理解体积的概念，并比较每个几何体之间的体积大小。

3.6种颜色，符合孩子的审美。

玩法：

1.认知几何体。这在学前班和小学和初中阶段都是常见的问题。

2.建立几何体和平面图形之间的关系。

3.理解体积的概念。在几何体里注水、做软陶模型用以理解体积概念、切面的概念、以及不同几何体的体积关系，然后进一步引导计算。

底面积相等、高相等的情况下，圆锥体积是圆柱体积的1/3。

切面：用软陶做模型，确认圆柱体的切面是四边形。

点评：

知识点含量非常多的一套教具，这也是在美国非常受欢迎的一套教具。细节精致，颜色鲜艳，孩子一见就爱不释手。

好啦，这就是我这次推荐的7套学校教具，它对接了小学数学中一些重要的基础知识点和能力培养点。

更为关键是，它们不抽象、更不枯燥，而是用具象的二维图形、三维立体，将知识展现的淋漓尽致、生动有趣，在“寓教于乐”中潜移默化地锻炼了孩子的视觉-空间能力，培养了他们的数学能力。

《美国科学院院刊》（PNAS）发表过一篇文章说：人类大脑中负责高难度数学问题的区域，与负责基本数感的区域基本相同。

法国认知神经科学家 Stanislas Dehaene的研究， 更是精确定位，就是负责视觉-空间那块区域（双侧顶叶下部）！

无论爱因斯坦一类史诗级人物的伟大发现，还是普娃计算的1 1=2，使用的是同样的大脑区域。

也就是说，我们既要呵护孩子天生的数学能力，又可以通过后天的训练来培养和提升它。

而在这里，“视觉数学”的意义显得愈加非比寻常，而好的方法、好的教具也变得更加必要和重要。

P.S.

我在检索视觉数学资料时，在外网上发现了一套教材，主要是提供给教师使用的，有完整的指导手册、教案和学生活动手册等内容。

目前涵盖了两个阶段的课程，分别面对5-6年级和6-7的学生（美国的年纪划分，我们可以适当降低标准）。有兴趣的亲们可以私信我“资料包”获得完整的资料包（全英文的）。

川妈说说

每次推荐教具、桌游等等，大家问的最多的是“团购吗？”“购买链接在哪里？”

有的时候，真的无能为力，比如两年前就推荐给大家的地产大亨。至今还有朋友留言问啥时组织团购。已经和品牌商直接、反复沟通过了，确定了，不会开团。

不是什么别的原因，只是因为价格，品牌要求我们开团的价格，比他们促销活动时价格还高！我们无法接受，所以请大家趁着618大促去孩之宝官方旗舰店看看吧，99元是我见过的最低价格（我说的是正品行货啊）。

这次可能会不同。推荐的7款教具中，Block by Block（堆砌大师）这周就会组织团购，因为品质价格都已经反复确认过；Saalin Tangram（七巧板）正确协商过程中，团购的概率比较高。

其他的，大家还想要的，点“在看”告诉我，或者留言告诉我具体看重哪些。我不能保证每个都能搞定，但一定会努力。

mom看世界：践行自然教育，追求自然养育，崇尚自然生活，期待更多的姐妹与我携手同行。对啦，目前我在“头条号、公众号”两个平台发布文章，名字均为【mom看世界】，欢迎关注。

,