七下二元一次方程组压轴题讲解（数学七下第二章）

哈喽，大家好！我们又见面了，欢迎继续关注【轩爸辅导】的【口袋数学】。日更【每日一学】【每日一练】，帮助孩子日积月累，考出好的成绩。配套辅导，哪里不会学哪里，哪里出错练哪里，帮助孩子提高效率。

【知识要点】

要点一、二元一次方程

含有两个未知数，并且含有未知数的项的次数都是1，像这样的方程叫做二元一次方程．

要点诠释：二元一次方程满足的三个条件：

（1）在方程中“元”是指未知数，“二元”就是指方程中有且只有两个未知数.

（2）“未知数的次数为1”是指含有未知数的项（单项式）的次数是1.

（3）二元一次方程的左边和右边都必须是整式.

要点二、二元一次方程的解

一般地，使二元一次方程两边的值相等的两个未知数的值，叫做二元一次方程的一组解．

要点诠释：

(1)二元一次方程的解都是一对数值，而不是一个数值，一般用大括号联立起来，如：

．

(2)一般情况下，二元一次方程有无数个解，即有无数多对数适合这个二元一次方程．

要点三、二元一次方程组

把具有相同未知数的两个二元一次方程合在一起，就组成了一个二元一次方程组.

要点诠释：组成方程组的两个方程不必同时含有两个未知数，例如

也是二元一次方程组.

要点四、二元一次方程组的解

一般地，二元一次方程组的两个方程的公共解，叫做二元一次方程组的解.

要点诠释：

(1)二元一次方程组的解是一组数对，它必须同时满足方程组中的每一个方程，一般写成

的形式．

(2)一般地，二元一次方程组的解只有一个，但也有特殊情况，

如方程组

无解，而方程组

的解有无数个．

【典型例题】

类型一、二元一次方程

【例1】已知下列方程，其中是二元一次方程的有________．

(1)2x-5＝y； (2)x-1＝4； (3)xy＝3； (4)x y＝6； (5)2x-4y＝7；

(6)

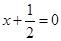
；(7)

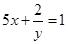
；(8)

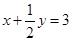
；(9)

；(10)

．

【思路点拨】按二元一次方程满足的三个条件一一检验．

【答案】(1)(4)(5)(8)(10)

【解析】只有(1)(4)(5)(8)(10)满足二元一次方程的概念．(2)为一元一次方程，方程中只含有一个未知数；(3)中含未知数的项的次数为2；(6)只含有一个未知数；(7)不是整式方程；(9)中未知数x的次数为2．

【总结升华】判断一个方程是否为二元一次方程的依据是二元一次方程的定义，对于比较复杂的方程，可以先化简，再根据定义进行判断．

举一反三：

【变式】下列方程中，属于二元一次方程的有（ ）

A.

B.

C.

D.

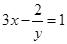
【答案】B

【例2】若

是关于x、y的二元一次方程，求a的值．

【思路点拨】根据二元一次方程的定义作答．

【答案与解析】

解：根据题意得：|a|-2＝1，所以|a|＝3，a＝±3，而(a-3)x中，a-3≠0，即a≠3，所以a＝-3．

【总结升华】二元一次方程和二元一次方程组中系数的求解，要同时考虑两个未知数的系数与次数，不管方程的形式如何变化，必须满足含有两个未知数，含未知数的项的次数是一次且方程左右两边都是整式这三个条件．

举一反三：

【变式1】已知方程

是二元一次方程，则m= ， n= .

【答案】-2，1/4

【变式2】方程

，当

时，它是一元一次方程．

【答案】

；

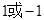
类型二、二元一次方程的解

【例3】二元一次方程x-2y＝1有无数多个解，下列四组值中不是该方程解的是( )

A．

B．

C．

D．

【答案】B

【解析】

解：当x＝0，y＝-1/2时，x-2y＝1，故A是原方程的解．

当x＝1，y＝1时，x-2y＝-1，故B不是原方程的解．

当x＝1，y＝0时，x-2y＝1，故C是原方程的解．

当x＝-1，y＝-1时，x-2y＝1，故D是原方程的解．

【总结升华】判断一组数值是否是原方程的解，只需要将这组数值代入原方程，能使方程左右两边相等的未知数的值是原方程的解，否则，不是．

举一反三：

【变式】若方程

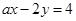
的一个解是

，则a= .

【答案】3

【例4】已知二元一次方程

．

(1)用含有x的代数式表示y；(2)用含有y的代数式表示x；

(3)用适当的数填空，使

是方程的解．

【思路点拨】用含一个未知数的代数式表示另一个未知数，就是把要表示的未知数当未知数，把其他的未知数当已知数，然后再将方程变形．

【答案与解析】

解：(1)将方程变形为3y＝2-x/2，化y的系数为1，得

．

(2)将方程变形为

，化x的系数为1，得

．

(3)把x＝-2代入

得， y＝1．

【总结升华】用含x的代数式表示y，其实质表示为“y＝含x的代数式”的形式．在进行方程的变形过程中，有效地利用解一元一次方程的方法技巧很重要．

举一反三：

【变式】已知：2x 3y=7，用关于y的代数式表示x，用关于x的代数式表示y．

【答案】

解：（1）2x=7－3y，

；（2）3y=7－2x，

【例5】写出二元一次方程

的所有正整数解.

【思路点拨】可以把二元一次方程中的一个未知数看成已知数，先解关于另一个未知数的一元一次方程，当两个未知数的取值均为正整数才是方程的解，写时注意按一定规律写，做到不重、不漏.

【答案与解析】

解：由原方程得

，因为

都是正整数，

所以当

时，

.

所以方程

的所有正整数解为：

，

，

，

.

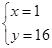
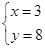
【总结升华】对题意理解，要注意两点：①要正确；②不重、不漏. 两个未知数的取值均为正整数才是符合题意的解.

举一反三：

【变式1】已知二元一次方程

，下列说法不正确的是（ ）

A.它有无数多组解 B.它有无数多组整数解

C.它有4组正整数解 D.它的解中不会出现负整数

【答案】D

【变式2】在方程

中，若y分别取2、1/4、0、－1、－4，求相应的x的值.

【答案】将

变形得

.

把已知

值依次代入方程的右边，计算相应值，如下表：

类型三、二元一次方程组及方程组的解

【例6】下列方程组中，是二元一次方程组的是（ ）

A.

B.

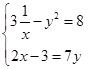
C.

D.

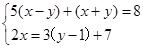
【答案】D

【解析】A，B中未知数的次数高于或低于一次，而C中出现三个未知数，只有D选项满足题意，故正确答案为D.

【总结升华】是否是二元一次方程组要满足“1、只有两个未知数；2、未知数的项最高次数都应是一次；3、都是整式方程”．

【例7】判断下列各组数是否是二元一次方程组

的解．

（1）

（2）

【答案与解析】

解：（1）把

代入方程①中，左边＝2，右边＝2，所以

是方程①的解．

把x＝3，y＝-5代入方程②中，左边＝

，右边＝-1，左边≠右边，所以

不是方程②的解．

所以

不是方程组的解．

（2）把

代入方程①中，左边＝-6，右边＝2，所以左边≠右边，所以

不是方程①的解，

再把

代入方程②中，左边＝x y＝-1，右边＝-1，左边＝右边，所以

是方程②的解，但由于它不是方程①的解，所以它也不是方程组的解．

【总结升华】检验是否是方程组的解，应把数值代入两个方程，若两个方程同时成立，才是方程组的解，而方程组中某一个方程的某一组解不一定是方程组的解.

举一反三：

【变式】写出解为

的二元一次方程组．

【答案】

解：此题答案不唯一，可先任构造两个以

为解的二元一次方程，然后将它们用“{”联立即可，现举一例：

∵ x＝1，y＝-2，

∴ x y＝1-2＝-1．

2x-5y＝2×1-5×(-2)＝12．

∴

就是所求的一个二元一次方程组．

注：任选的两个方程，只要其对应系数不成比例，联立起来即为所求．

【例8】(淮阳)甲、乙两人共同解方程组

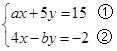
由于甲看错了方程①中的a，得到方程组的解为

．乙看错了方程②中的b．得到方程组的解为

．试计算：

的值．

【思路点拨】把x、y的值代入正确的方程，就可以求出字母的值．

【答案与解析】

解：把

代入②，得-12 b＝-2，所以b＝10．

把

代入①，得5a 20＝15，所以a＝-1，

所以

．

【总结升华】一组数是方程的解，那么它一定满足这个方程，利用方程解的定义可以求出方程中其他字母的值，所以在今后的学习中要会灵活运用它．

举一反三：

【变式】已知关于

的二元一次方程组

，求

．

【答案】

解：将

代入原方程组得：

，解得

， 所以

．

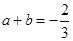
转载请注明：轩爸辅导 » 数学七下，第二章，二元一次方程组的概念，知识要点和典型例题

,