平衡二叉树的树高是多少（查找二叉树最优二叉树）

查找二叉树

又叫二叉排序树

性质：左儿子的值 < 父结点的值 < 右儿子的值

因此，不能存在俩个相同值的结点

作用（意义)：极大程度提高查询数据的效率。（相当于二分查找的效率）

插入结点：

1. 若有相同键值的结点，则不插入。
2. 若查找二叉树为空，则直接作为根结点。
3. 与父结点（先从根结点）比较。小于父结点，插入结点到左子树。大于父结点，插入结点到右子树。

删除结点：

1. 如果为叶子结点，直接删除。
2. 如果只有一个儿子结点，则让儿子结点代替它的位置。
3. 如果有俩个儿子结点，则在该结点的左子树上，找到最大键值的结点S，把该结点的值变为结点S的值，然后删除结点S。（相当于找到比它第一小的结点，代替它的位置）

最优二叉树（哈夫曼树）

是一个工具人工具树

用于哈夫曼编码

哈夫曼编码 ：压缩编码方式，使原始信息的编码长度变短，用来节省存储空间和传输带宽。在多媒体压缩中常用到，属于无损压缩。

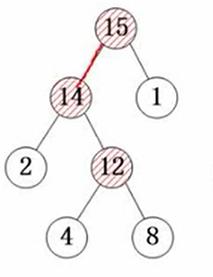
基本概念

叶子结点才有实际意义！！！非叶子结点是建树时的工具 （工具人的工具）

• 树的路径长度：把所有的路径累加起来的长度。
• 权：叶子结点上的值，代表某一个字符出现的频度。
• 带权路径长度：把路径长度乘以权就是带权路径长度。（如2结点的带权路径长度为 2 （路径长度）* 2（权） = 4）
• 树的带权路径长度 又叫树的代价：所有叶子结点的带权路径长度相加，就是整棵树的带权路径长度。

构建哈夫曼树，就是为了让一棵树的带权路径长度最短。

建树过程：

过程相当于经典问题石子合并

如例题：

有一组权值的结点为{5，29，7，8，14，23，3，11}

while(结点数量大于一){ 选出最小的俩个结点（包括以他们为根结点的树） 合并到一个新的父结点上，新的结点的值为他们俩的值之和 }

过程

现在有结点： { 5，29，7，8，14，23，3，11 }

1. 先选择5和3，合并到一个新结点为8.现在有结点： { 5 ，8，29，7 ，8，14，23，3，11 }

2. 再选择8和7，合并到一个新结点15.（有多个相同值结点时，选哪个都可以，也就是说哈夫曼树不唯一）现在有结点： { 8 ，29，7，15 ，8，14，23，11 }

3. 再选择8和11，合并到一个新结点19。现在有结点： { 29，15，8，14，23，11 ，19}

4. 再选择15和14，合并到一个新结点29。现在有结点： { 29，15，14，29，23，19}

5. 再选择23和19，合并到一个新结点42。现在有结点： { 29，29，23，19，42}

6. 再选择29和29，合并到一个新结点58。现在有结点： { 29，29，58，42}

7. 再选择58和42，合并到一个新结点100。现在有结点： { 58，42，100}

对于这棵树的带权路径长度为：

55 35 74 143 83 113 292 232

线索二叉树

概念：在原有的二叉树上，混有虚线的箭头。

为什么有线索二叉树：我们都知道，在二叉树里每个结点需要有三个空间，指向左结点的指针，指向右结点的指针，自己存的值。但是！ 在二叉树中，叶子结点和只有一个儿子的父结点总有空间被浪费掉了。线索二叉树就是把这些浪费的空间利用起来。

利用起来干嘛呢？利用起来方便遍历，加快遍历的速度。

具体实现线索二叉树又分为：前序线索二叉树、中序线索二叉树、后序线索二叉树。

前序线索二叉树：空闲的左指针指向前序遍历中的上一个结点，空闲的右指针指向前序遍历中的下一个结点。中序线索二叉树：空闲的左指针指向中序遍历中的上一个结点，空闲的右指针指向中序遍历中的下一个结点。

后序线索二叉树：空闲的左指针指向中序遍历中的上一个结点，空闲的右指针指向中序遍历中的下一个结点。

平衡二叉树

概念引入：在排序二叉树（查找二叉树）中，我们发现同样序列中，不同结构的排序二叉树查找效率不一样。

并且一个排序二叉树越平衡，它的查找效率越高。平衡：任意的结点的左右子树深度差越小，就说这个排序二叉树越平衡。

如：图1与图2的序列相同，但因为图1比图2平衡，所以图1的查找效率比图2高。

图1

图2

而！平衡二叉树 就是同一个序列中，非常平衡的二叉树。

定义：

• 任意结点的左右子树的深度相差不能超过1。
• 每结点的平衡度只能是 -1、0、1.

深度 ：有多少代子孙就是多少深度。叶子结点深度为0.平衡度：

• 左子树深度减去右子树的深度。
• 叶子结点的平衡度为0。