数学史微积分的进一步发展（带你读大清微积分）

编辑：小咸鱼 好困

【新智元导读】你有见过160多年前清朝数学家写的微积分书吗？这可能是最难懂的高数教材了，堪称天书！近日，网上流传着一本清朝的微积分课本，其中的所有数学表达式都是用文言文书写的。小编不才，斗胆翻译了一下，看看这天书里面到底写了些什么。

看到这些密密麻麻的数学式子，有唤起那种被高等数学微积分支配的恐惧了吗？

其实，微积分不仅「折磨」着一代又一代大一刚开学的新同学们，早在清朝的时候，就已经开始折磨人了！

大清？

是的，清朝的数学家李善兰将国外的微积分课本直接翻译成了文言文，供人们参考学习。

快看看，什么叫文言文 微积分的双重酸爽。这酸爽，才够味！（战术后仰）

5分钟带你读清朝微积分

首先，你可以用文言文的知识去读一下，看看能看懂多少。

好吧，放弃抵抗了，文言文的知识根本不够用啊！

这里面怎么还有像是自己造的字呢？比如双人旁一个天，是什么鬼东西？

这里就不得不引入几条先验知识：

1. 「分数」的「分子」是分母，「分母」是分子 。也就是说，如果看到「分数」，则它的倒数就是现代意义下的分数。
2. 彳= d, 天 = x, 戍 = y，那么彳天 = dx, 彳戍 = dy
3. 一 = 1
4. 訥 = ln
5. 丄 =

所以，「戍=天^天」这句话的意思就是

。

这里，

。

而

因此，

而「彳戍=天^天（一丄訥天）彳天」就是 「dy = x^x (1 lnx) dx」，确实可以由上面那个式子整理得到。

两个简单公式的破译就搞定了，对号入座即可。

接下来就比较难了。

首先，先要明确

这个概念是什么。

天和地在这里就不能理解为简单的x和y了，而是应该理解为f(x)与g(x)两个关于x的函数。

换句话说，就是对

求导。

首先将

改写为：

。

求导就会得到：

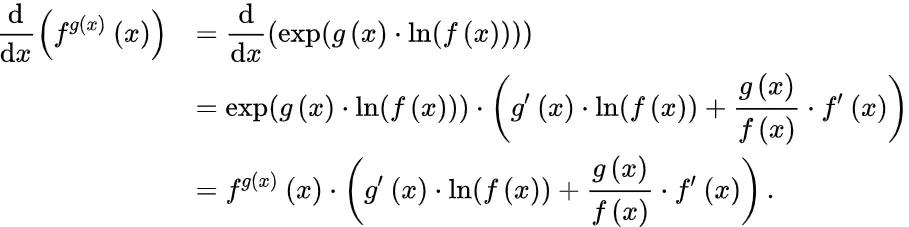
将

代入式子，将dx换到右边：

dx可以与

、

合并变成dg和df，所以：

将

除到左边：

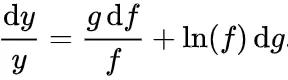
根据「分子」是分母，「分母」是分子、戍 = y、天= f(x)、地= g(x)的原则，就会发现，

和上面的式子一模一样。

这样第一页就完全破译了，至于后面的几页就交给爱钻研的勇士们，小编的脑细胞已经阵亡了。。。

中国第一本微积分课本

李善兰（1810年－1882年），字壬叔，号秋纫，清朝数学家。浙江省杭州府海宁县人。为清代数学史上的杰出代表，中国近代数学的先驱。

李善兰于清嘉庆十五年（1810年）1月2日生于浙江海宁县硖石镇。10岁即通《九章算术》，15岁通习《几何原本》六卷，17岁参加杭州乡试未中。从此钻研天文、历算，成为远近闻名的数学家。

1852年－1866年李善兰受聘於墨海书馆任编译。同治二年（1863年）被招至曾国藩幕中。

同治五年（1866年）曾国藩出资三百金为李善兰刻《几何原本》后九卷。

1868年，李善兰入同文馆总教习，执教算法，前后八年。同治十三年（1874年）升户部主事。光绪二年（1876年）升员外郎。光绪八年（1882年）升郎中。

李善兰在1859年与英国传教士Alexander Wylie合作，翻译了Elias Loomis的「Elements of Analytical Geometry and of the Differential and Integral Calculus」（1850）。

英文原著到1859年为止，已经出版到第10版，足以见得它相当受到大学教师的青睐。

作者，Elias Loomis为LL. D（法学博士），在出版这一本教科书时，正担任纽约市立大学的数学与自然哲学教授 (Professor of Mathematics and Natural Philosophy, the University of the City of New York)。

Loomis表示，本书「并非为了数学家、也不是为了那些拥有特殊天分或是数学的爱好者，而是为广大中等资质的大学生而写。」这或许也是英文原版畅销的原因之一吧。

本书的中文译名为「代微积拾级」，强调本书依序讲述「代（数）」（解析几何）、「微（分）」与「积（分）」，「拾级」而上。

「微分积分，为中土算书所未有，然观当代天算家，如董方立氏、项梅侣氏、徐君青氏、戴鄂士氏、顾尚之氏，暨李君秋纫，所著各书，其理有什近微分者，因不用代数式，或言之甚繁推之甚难，今特偕李君译此书，为微分积分入门之助。」

上引文提及之天算家依序为董佑城、项名达、徐有壬、戴煦、顾观光以及李善兰，都是十九世纪中国清代数学名家。

不过，由于「不用代数式」，所以文章显得「言之甚繁，推之甚难」。

在本书中，英文原文中的 analytical geometry（解析几何）一概翻译为「代数几何」。

微分有七卷（卷十到十六）。

其中，Loomis主要运用微分系数（differential coefficient）来表示我们今日所谓的导数（derivative）。

「函数与变数之比例，俱谓之微分，用ㄔ号记之。如戌 = 天三，则得比例ㄔ天 : ㄔ戌 :: 一 : 三天二。ㄔ天、ㄔ戌为天与戊之微分。后皆仿此。用表天与戌之变比例，以一、四两率相乘，二、三两率相乘则得ㄔ戌 = 三天二ㄔ天，此显函数戌之变比例，等于三天乘变数天之变比例，以ㄔ天约之得ㄔ天/ㄔ戌 = 三天二。此显变数之变比例约函数之变比例，等于函数之微系数也。」

「ㄔ天 : ㄔ戌 :: 一 : 三天二」也就是「dx:du=1:3×2」。

由于分子、分母的位置，是反着的，于是，du/dx对应为ㄔ天/ㄔ戌。

根据上述引文，针对任何一个函数 y=f(x) 而言，先求出 dy=f(x)dx，然后再得到 dy/dx＝f(x)。

如此，就可以避开导数定义中，[f(x h)−f(x)]/h分子与分母同时趋近于零的难题。

在Karl Weierstrass的分析算术化（arithmetization of analysis）提出的极限ε−δ定义之前，是无法解决的。

此外，本书还有一个特点：相对于七卷的微分内容，积分只有两卷！

《积分一总论》一开始内容如下：

「积分为微分之还原，其法之要在识别微分所由生之函数，如已得天二之微分为二天ㄔ天，则有二天ㄔ天即知所由生之函数为天二，而天二即为积分。已得微分所由生之函数为积分，而积分或有常数附之，或无常数附之，既不能定，故式中恒附以常数，命为口丙，口丙或有同数或为0，须考题乃知。来本之视微分若函数诸小较之一，诸小较并之，即成函数，故微分之左系一禾字，指欲取诸微分之积分也。如下式禾二天ㄔ天=天 口丙。来氏说，今西国天算家大率不用，而惟用此禾字取其一览了然也。」

在上述引文中，李善兰将积分∫则译为「禾」。此外，Loomis未曾独立地定义定积分（definite integral），而是通过不定积分（indefinite integral）来定义，省去了定义定积分的麻烦。

怎么样，有兴趣挑战一下清朝的微积分吗？

参考资料：

https://www.bilibili.com/video/BV1RR4y1t7AH?from=search&seid=8170464341069800644&spm_id_from=333.337.0.0

https://www.reddit.com/r/China_irl/comments/r0xh97/清朝微积分课本/

https://highscope.ch.ntu.edu.tw/wordpress/?p=25200

本文引用了以下知乎作者的文章：

「zdr0」https://zhuanlan.zhihu.com/p/437864462

,