最常用的哈希算法（一致性哈希算法简介）

一致性哈希算法（Consistent Hashing）最早在1997年由 David Karger 等人在论文《Consistent Hashing and Random Trees: Distributed Caching Protocols for Relieving Hot Spots on the World Wide Web》中被提出，其设计目标是为了解决因特网中的热点(Hot spot)问题；一致性哈希最初在 P2P 网络中作为分布式哈希表（ DHT）的常用数据分布算法，目前这个算法在分布式系统中成为使用较为广泛的数据分布方式。

一致性哈希算法原理

一致性哈希算法的实现原理其实很简单，其将整个哈希值空间组织成一个虚拟的圆环，比如某哈希函数H的值空间为0-232-1（即哈希值是一个32位无符号整形），那么整个哈希空间环看起来就像下图所示：

整个空间按顺时针方向组织，由于是环形空间，所以0和232-1实际上是重叠的，上图只是为了表示方便没有画到一起。

将机器映射到环中

一致性哈希算法是数据分布的方式，而数据最终是需要存到机器中的，所以我们首先需要将机器映射到环中。假设我们有四台机器 N1、N2、N3 以及 N4，我们使用机器名或者 ip 计算这些机器的哈希值，然后分别映射到环中去，看起来就像下面一样：

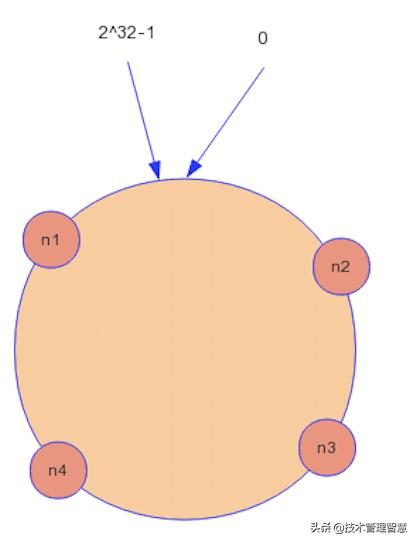
将数据映射到环中

我们使用相同的哈希函数计算需要存储数据的哈希值，假设现在我们有四份数据 d1、d2、d3 以及 d4，我们需要将这些数据映射到环中去，这样看起来像下面图一样：

在这个哈希环中，数据存储的机器是按照顺时针方向遇到的第一个节点就是这个数据存储的节点，所以图中：

• 数据 d1 存储在节点 N2 上；
• 数据 d2 存储在节点 N3 上；
• 数据 d3 存储在节点 N4 上；
• 数据 d4存储在节点 N1 上。

添加节点

在分布式环境中，添加或减少节点是很常见的操作。现在我们往上面的哈希环添加一个节点 N5，同样使用相同的哈希函数计算这个节点在哈希环的位置，假设计算的结果如下：

添加节点 N5 之后，原本存储在 N4 上的数据 d3 就分配到 N5 了，其他数据分配不变。相比于普通的哈希添加节点会导致大量映射失效，一致性哈希可以很好的处理这种情况。如果增加一台服务器，则受影响的数据仅仅是新服务器到其环空间中前一台服务器（即沿着逆时针方向行走遇到的第一台服务器）之间数据，其它数据也不会受到影响。

删除节点

如果哈希环中有节点出现故障，需要从哈希空间中移除，那么影响的数据也是有限的。假设节点 N3 出现故障需要移除，新的哈希空间的数据映射如下：

N3 节点移走之后，数据 d2 就存储到 N4 节点上了。所以如果从环中删除节点，受影响的数据仅仅是此服务器到其环空间中前一台服务器（即沿着逆时针方向行走遇到的第一台服务器）之间数据，其它不会受到影响。

虚拟节点

上述最基本的一致性哈希算法有很明显缺点，随机分布节方式使得难均匀的分布哈希值域；尤其在动态增加节点后，即使原先的分布均匀也很难保证继续均匀。由此带来另一个较为严重的缺点是，当一个节异常时，该节点的压力全部转移到相邻的一个节点，当加入一个新节点时，只能为一个相邻节点分摊压力。

为此一个改进方法是引入虚拟节点（virtual node ），虚拟节点是实际节点在哈希空间的复制品（ replica ），一个实际节点（机器）对应了若干个虚拟节点，这个对应个数也成为复制个数，虚拟节点在哈希空间中以哈希值排列。

为了表述方便，假设我们有2个节点，4份数据，在引入虚拟节点之前节点和数据分布如下：

可以看见节点 N2 管理的数据有 d1；而节点 N1 仅仅只管理数据 d2、data3 和 data4。这就造成了数据分布不均匀的情况。如果我们通过引入虚拟节点，并且假定复制个数为2，则哈希之后的情况如下：

其中 N1.1、N1.2 是 N1 虚拟出来的节点；同理N2.1、N2.2 是 N2 虚拟出来的节点。通过添加虚拟节点之后，各个节点管理的数据已经比较均匀了。