滴滴出行快车预估准吗（的预测准确率覆盖30）

作者｜张凌宇

编辑｜小智

“猜你想去”是滴滴出行大数据智能预测体系的主要功能之一。通过此功能，滴滴可为一些大型商超、火车站等人流密集场所提供出行解决方案建议。目前“猜你想去”功能已覆盖了滴滴平台上 30% 的订单，预测准确率达 90%。与“猜你想去”功能相关的专利也已提交受理。

1 写在前面

滴滴的“猜您去哪”目的地预测系统是我们的一个非常酷炫的系统，背后有着强劲的算法和技术支撑。

当用户打开滴滴出行 app 的时候，如果我们的系统能够猜用户即将去往的目的地，就会填写到“猜您要去”的框中。大多数用户评论这个功能的时候，都会说我们猜的是准的，很酷炫。

这个功能有什么用呢？我们在设计这个功能的时候，有这么几个出发点：一是要能方便用户，降低用户发单时候的输入成本；二是要惊艳用户，彰显滴滴的人工智能科技，以 90% 以上的准确率，预测 30% 以上的出行；三是预测人群的出行流向，从而更好的规划交通运力。

下面会从我们问题定义、模型抽象、用数据统计求解模型以及数据分享等几个方面进行介绍。

2 定义问题：从业务场景到模型抽象

研发工程师每天都会面对的一个场景，就是产品经理提需求。当时我们是把需求定义成这样一个问题：通过用户的出行历史，预测用户当前时间、当前地点下的出行目的地。

有了问题定义之后接下来就是要把这个问题抽象成预测模型。T 是当前时间，S 是当前位置，X 是预测目的地，我在当前时间、当前地点出发，在这个条件下用户即将去往的那个目的地条件概率应该是远远大于他去其他地方的概率。比如说今天晚上九点我在酒店打开滴滴出行 APP，如果查出我去虹桥机场的远远大于外滩的概率，那么这个系统就猜去我去虹桥机场。这是一个条件概率的问题。

3 从 0 到 1 快速搭建模型：基于互信息选择主要特征

有了模型之后，我们由简单到复杂地从 0 到 1 快速搭建系统。目的地是待预测的变量，时间变量是一个复合变量，包含日期和时刻，比如日期为 2016 年 8 月 23 日，时刻是 18 点 10 分。地址变量也是复合变量，包括地址名称和经纬度。这些变量又包含不同的类型，比如说地址名称，是一个离散型的随机变量，经度和纬度是连续性变量，时间是周期型变量，经度和纬度两个联合起来又是一个二维的联合变量。把所有这些变量都用起来，让每个变量都充分发挥它的功能，是我们要研究的长期课题。而现阶段，我们的目标是快速搭建一个系统，快速上线。

这个时候，面对这么多特征，我们需要做的首先是选择一个主要特征。特征选择的原则，是选择和被预测变量最相关的特征。通常，度量变量之间的相关性的指标是皮尔逊系数和互信息。皮尔逊系数通常用来衡量两个连续型随机变量的相关性，计算出来的结果是线性相关性。刚才我们说到我们的备选特征既有连续型，也有离散型，还有周期型和复合型的，所以在这我们选择了互信息来衡量变量之间的相关性。因为我们的目标是目的地，待选特征先圈定了出发地、出发时刻、出发时期这三个变量。

如图所示，最左边是目的地和出发地，中间是目的地和出发时期，最右边是目的地和出发时刻，数值最高的是目的地和出发时刻两个变量间的互信息值。这也符合我们的认知：一般情况下，我早上打开滴滴出行的时候，往往出行的目的地是公司，如果是晚上打开，目的地可能就是我的家。所以我们得到的结论就是出发时刻这个特征是预测目的地最好的单一特征。

接下来这个问题就进一步简化为，计算在出发时刻这个特征下每个目的地的条件概率，这样一个概率模型。这也就是贝叶斯估计的概率问题，根据贝叶斯公式和全概率公式转换一下，关键要求解的变量，就是在目的地这个条件下出发时刻的概率分布。

4 关键问题求解：从数据中发现规律

下面介绍下关键问题的求解。我们先看一个用户的数据，下表最左边一列都是用户的出发时间，右边是对应的目的地。

这样的数据可能不太容易看出规律来。刚才说统计时刻特征，所以把日期去掉，左边是目的地，右边是发单时刻。这样可能还是不太容易看出规律。

下面是我绘制目的地 A 的出行频率的直方图。这么一看就非常明显了。这个分布非常像经典的数据统计里的正态分布，也叫高斯分布。我们分析了很多个 case 之后发现都跟这个类似，也就是同一用户、同一目的地是符合正态分布的。

接下来的问题就是，我们如何去估计这个正态分布。我们知道，正态分布有两个关键参数，一个是期望一个是方差，接下来就是我们如何去估计均值和方差。

我们先看两个例子。第一个例子，时刻分别是 8 点、9 点、10 点，所以均值是 9 点，这个直接得到结果了。下一个时刻分别是 23 点、0 点、1 点，均值是 0 点。留一个计算题给各位，3 点、22 点、23 点，均值是多少？3 点、15 点、21 点均值是多少？

在这里我介绍两种方法，第一种方法是向量法。

下图是一个圆的表盘，有两个坐标轴，x 轴和 y 轴。每一个时刻用向量表示，然后求和向量。刚才问题里的 3 点、22 点、23 点三个点的和向量是 0，所以均值是 0。

整个算法的流程是这样，首先计算每一个时刻对应的向量表示，也就是把每个时刻转换成向量角度。分别计算它的正弦余弦值，来表示它的 x 轴、y 轴坐标。第二步计算 n 个时刻对应的和向量。第三步计算和向量与 x 轴的夹角，用反余弦公式。第四步把夹角转换为对应的时刻，也就是我们要计算的均值。最后计算对应的方差。

但是这个向量法是有两个小问题的：

看这么两个例子，第一个例子，如果三个时刻是 0 点、0 点、3 点，用向量法计算的均值是 0 点 58 分 33 秒，但实际上它的均值应该是 1 点。另外一个例子是，如果两个时刻 0 点和 12 点，转换成向量互为反向量，加和是零向量，零向量是没有方向的，也就是无解的。那么问题来了，向量法只能得到近似解，并且在边界情况下无解，我们该怎么办？

我介绍的第二个方法是拉格朗日法，能解决这个问题。我们先回顾下算术平均值的概念和性质，算术平均值满足这么一个重要性质：它与所有观测样本的距离平方和最小。怎么求解？就是拉格朗日法。

先对方程求导，让导数等于 0，得到一个新的标红的公式，这个公式就是我们熟知的算数平均值的计算公式。

类比一下，平均时刻也可以表示成这个样子，平均时刻可以认为是与所有时刻距离平方和最小的那个时刻。这里引入了一个新的概念，就是两个时刻的距离。那怎么去计算两个时刻的距离？我先看两个时刻的距离应该满足的两个性质：首先两个时刻的距离不能是负值，必须大于等于 0；另外是两个时刻的距离不能超过 12，也就是 23 点和 0 点，它们的距离是 1 而不是 23。有了这两个之后，可以用下面这个分段函数。

这个分段函数不太容易代入到上面的问题进行求解，没有关系，可以用绝对值的性质再转化一下就推出了统一的表达式，这时候这两个分段函数就统一了。

最后代入到上面的优化问题里面，然后解这个优化问题我就能得到时刻和方差，这个是任何时候都有解的，并且解是精确解。关于这个模型求解由于时间关系我就不展开了。

总结一下，向量法简洁，容易理解，但是它求的是近似解，而且边界条件下无解。拉格朗日法得到的是精确解，但直观上不好理解，求解算法略复杂，时间复杂度是 O(nlogn)。

最后还有一个问题，上面我有假设同一用户、同一目的地下出发时刻符合正态分布。这里是有点小问题的，正态分布自变量的分布是整个数轴，从负无穷到正无穷。但出发时刻的分布是 0 到 24，并且有周期循环性。在高级的数理统计里面，这种分布叫循环正态分布，也叫冯·米赛斯分布。

下面是我们整个算法的流程，首先根据用户的历史订单，依次计算每个目的地对应的发单时刻的期望和方差；然后根据当前时间计算每个目的地概率的中间数据；第三步用贝叶斯框架计算每个目的地的概率；最后确定阈值，满足阈值的就是我们要的计算结果。

接下来我举一个形象点的例子。这个表是一个用户去每个目的地的出发时间分布，最右边是他的分布指标。

我把每个小时都转换成小数，比如说目的地 A，我们看到均值是 10.5，意思就是 10 点半，方差是两个小时，频率是 0.47。假设当前时间是早上 9 点，下面是中间的一些计算结果。

最后用贝叶斯公式转换一下，得到当天时间 9 点这个用户去 A 的概率是 0.98，如果阈值设置的是 0.9，那么目的地 A 就是我们“猜您要去”的结果。

5 精益求精：模型的进一步调优与优化

简单的模型之后，下一步我们要追求更好的效果，也就是要一步步把这个模型做的越来越复杂。首先我们看另一个单一的特征，这次不选出发时刻了，选出发地经纬度。下面是一个用户出发目的地出发经纬度的聚合，这个特征也具有正态分布的性质，有一个中心点，离这个中心越来越远，对应的频次会越来越低。

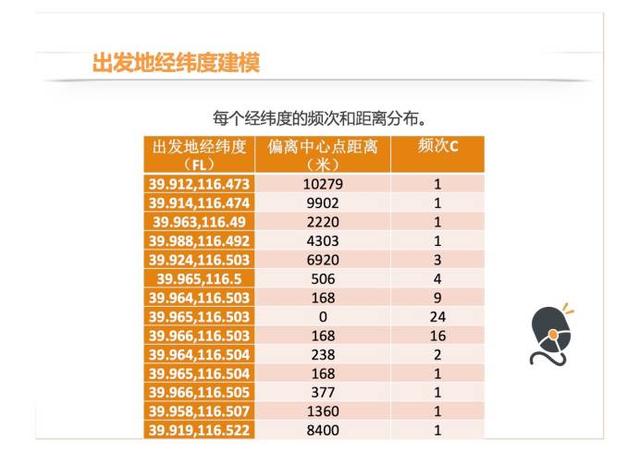
画一个三维图像就是这样子，所以说我再提一个假设，同一用户同一目的地下的出发地经纬度符合二维正态分布，具体密度函数是下面的公式。

每个参数我就不解释了，重点的推导过程我也不推了，其实跟我上面讲的出发时刻一样，算出概率来，最后套贝叶斯公式。

直接看结果，这是我选的用户，用出发地经纬度建模之后，如果这个用户从最右边的经纬度出发，他去几个目的地的概率。他去目的地 A 的概率最高，0.81。如果阈值选的是 0.9 的话，因为没有一个目的地的概率是高于 0.9 的，这种情况下，这个用户虽然打开 app 了，但并不会出现“猜您要去”，表示我们并没有充分预测出来他要去哪。

经过上面的研究讨论，我们能得出下面两个结论：一是同一用户同一目的地下的他的出发时刻是符合一维的正态分布的，二是同一用户同一目的地对应的出发经纬度是符合二维正态分布的。所以能推导出同一用户同一目的地出发时刻和出发经纬度符合三维正态分布。

我计算这三个变量的期望向量，以及协方差矩阵以及逆矩阵得到一个参数，然后套用贝叶斯公式。我们发现目的地 A 的概率最高，刚才是 0.81，现在是 0.97。也就是增加一个变量之后，系统预测出来的即将去往的目的地结果不确定性降低了。

前面我基本是用贝叶斯框架 正态分布这些传统的数理统计的知识，对业务进行建模。用三元正态分布的时候处理起来就已经比较复杂了，一般对传统的数理统计方法来说如果你有几十个特征的话那就是灾难了。

接下来我尝试从正态出发，套用贝叶斯框架，推导出一个机器学习的经典模型 LR 模型，代入我们系统，进入到机器学习时代。

我做了这么一个变量设定，用 D 表示特定目的地，Y 是目的地取值。

上面这两个方程的含义，可以具象为一个用户去 D 类目的地和不去 D 类目的地的正态分布。要估计的是用户在 X 这个特征下去 D 这个目的地的概率，套用贝叶斯公式变换一下，得到下面的式子。

其实这一块无非是线性代数的一些计算。把括号里面的东西展开合并，再做一些变换，最后得到的公式就比较简单了，就是逻辑回归的方程。

这里有几个需要注意的点，对比标准的逻辑回归，我用正态分布 贝叶斯框架推导出来的逻辑回归有二次项和交叉项。再一个，最初假设符合两个正态分布，而实际上不一定符合正态分布，甚至你很难找到一种分布去拟合。

如果我不对特征进行处理，而直接套用逻辑回归机器学习方法的话，得到的效果可能还没有传统的数理方法效果更好，所以要对特征进行一些工程化处理，就是特征工程。

接下来简单介绍一下我们机器学习特征工程的处理方法。特征工程是很大的课程，没有办法深入交流，我只简单介绍一下我们是怎么做的。

首先要进行一些特征筛选，在这里，因为我们被预测的变量是目的地，我们要选择跟目的地相关性很高的特征，比如出发时间、出发地以及用户信息，这是相关性比较高的特征。选出初始的特征之后下一步就要对这个特征进行拆分，通常的方法是利用业务常识，把选出来的特征拆分成更多粒度更细的子特征，比如把时间拆分成时刻来。对另外的一些特征可能我们需要进行深入的挖掘，比如说用户特征实际上是隐藏在用户行为背后的很多隐藏特征，这个时候我们有专门的数据挖掘团队，对用户特征进行用户画像或者用户行为分析。

拆分出来这么多特征之后，这些特征之间可能相互之间不独立，需要对特征做进一步提取和变换。选出特征之后，如果要用逻辑回归，那么可能还需要数据进行离散化，离散化成 0、1 变量。离散化主要是解决特征的增长，每个特征的增长可能对最后的结果贡献不是线性的，同时离散化成 0、1 变量之后线下训练的权重被线上系统加载之后能够直接使用，相当于把乘法直接转为加法，能够使系统的性能得到很大的提升。

6 数据之美：分享几个有意思的 case 的数据分布

以上主要是介绍了技术，接下来咱们一块看几个比较有意思的 case，感受一下我们滴滴数据的魅力。

第一个用户，他的数据只用出发时间这一个特征就能够很好的区分他去往哪个目的地。他去目的地 A 的平均出发时刻是 10.5，他去目的地 B 的平均出发时刻是 19 点 20，我画的图里面，蓝色就是去目的地 A 的出发时刻分布，红色是去目的地 B 的出发时刻分布，两个分布几乎没有交集。

目的地和出发时刻的互信息是很高的，1.36。目的地和出发时刻、出发地这两个变量的联合变量的互信息是 1.47。我们能看到，对这个用户来说，即使增加目的地特征，信息增益也没有涨多少。

第二个用户，用出发时刻不太能区分他去哪个目的地。他去目的地 A 的平均出发时刻是 12.4，他去目的地 B 的平均时刻是 11.6，这两个时间比较接近。这个用户在 12 点左右的时刻，我们发现他去目的地 A 和目的地 B 的概率都比较高，不太好区分，概率分布曲线有很大的交集。

下边是他去目的地 A 和目的地 B 对应的出发地经纬度分布，横轴是纬度，纵轴是经度。蓝点是这个用户去目的地 A 的经纬度，集中在一个区域；红点是这个用户去目的地 B 的经纬度，集中在另外一个区域。我们发现我们用他的出发地经纬度可以很好的区分他是去 A 目的地还是 B 目的地。

对这个用户，我们一次计算了他的目的地跟他对应的出发地、出发时刻以及出发地出发时刻联合变量的互信息，目的地和出发时刻的互信息是最高的。

上面是这个用户的出行历史，如果这个用户从 B 这个地方出发的话，多数情况是去 A，如果这个用户是在 A 这个地方出发的话多数情况是去 B，我们猜测这个人可能是中午下班的时候用我们的 APP 打车从 A 地打车到 B 地吃饭，然后吃完饭之后他再用我们的 APP 打车从 B 地到 A 地，而且他吃饭时间很快。这是个挺有意思的 case。

最后一个 case，出发时间和出发地的单一特征都不容易区分，我们可以看一下它的互信息。他的目的地和出发地的互信息不高，目的地和出发时刻的互信息也不高，但他的目的地和出发地、出发时刻两个联合变量的互信息就比较高了。对这个用户来说，用出发地和出发时刻两个变量联合出来，就可以知道他去哪里。我们直接看一下这个列表，如果这个用户是 18 点左右，并且他从 A 地出发的话，他很大概率是去 B 地。

本文分享的主线基本是按照滴滴“猜您要去”目的地预测系统，从无到有从有到优的顺序介绍的。另一条隐含的线是从数理统计到机器学习，前半部分我用传统的数理统计方法讲解了怎么建模，后半部分我们用现在的人工智能的潮流，用机器学习在这里建模，希望今天的分享给大家在工作和学习中带来一定的启发。谢谢大家。

作者介绍

张凌宇，2012 年加入百度，任搜索策略算法研发工程师；2013 年加入滴滴，高级算法工程师、出租车策略算法方向技术负责人、策略模型部资深技术专家，利用机器学习和大数据技术设计并主导实现了多个公司级智能系统引擎，如基于组合优化的订单分配系统、基于密度聚类与全局优化的运力调度引擎、流量引导与个性化推荐、“猜您去哪”个性化目的地推荐系统等。参与公司十多项技术创新专利研发、申请。擅长利用数学建模、业务模型抽象、机器学习等解决实际业务问题。

智能化运维、Serverless、DevOps、AIOps......CNUTCon 全球运维技术大会将于 9 月 10-11 日在 上海光大会展中心大酒店 举办，12 位大牛联合出品，揭秘智能时代下的新运维，更有 Google、Uber、eBay、IBM、阿里、百度、腾讯、携程、京东、华为等知名互联网公司一线技术大咖分享他们在最新运维技术实践过程中遇到的坑与经验，推荐学习！点击 「 阅读原文 」了解更多精彩！8 折报名倒计时一周，欲购从速！

今日荐文

点击下方图片即可阅读

如何挖掘 Nginx 日志中隐藏的金矿？

【原标题：90%的预测准确率覆盖30%的订单，滴滴出行“猜您要去”目的地预测系统是怎么做的？】,