阿基米德教你学数学（阿基米德数学之神）

巴勒莫大教堂（局部），作者摄。

上帝乃几何学家。——柏拉图

作者 | 蔡天新

来源 | 赛先生（ID：mrscience100）

01 叙拉古城

公元前287年，阿基米德出生在地中海最大的岛屿——西西里东南港市叙拉古（又译锡拉库萨），这个年份是依据他的死亡年份和寿命推算出来的。

12世纪的君士坦丁堡（今伊斯坦布尔）诗人、历史学家策策斯（Tzetzes）被认为是学究的完美典范，这位诗人的母亲是格鲁吉亚人，年轻时担任省长秘书，后来以教书和写作为生。他最著名的一部拜占庭重音（教诲）诗集《千千诗集》（又名《史书》）共一万二千多行，引用作家达四百多人，包含了许多轶文。其中提到，“智者阿基米德是叙拉古人，著名的机械制造师，终生研究几何学，活到七十五岁。”

叙拉古的奥提伽岛，阿基米德在此抗击罗马人。

阿基米德原本是有传记的，作者是他的一位叫赫拉克利德（Heraclides）的朋友。赫拉克利德与公元前6世纪的哲学家赫拉克利特（Heracleitus）不是同一个人，也非同一个时代。还有一位公元前4世纪的天文学家赫拉克利德斯（Heracleides）名字也很相近，后者是柏拉图的学生和学园管理者，曾率先提出地动说，并认为水星和金星是绕日旋转的。6世纪的数学注释家欧托基奥斯（Eutocius）曾不止一次提到这本传记，可惜后来失传了。阿基米德的生平事迹，如同米利都的泰勒斯一样，散见于古代的各种文献中。

古希腊共有四个主要部落，分别是亚加亚人（迈锡尼人）、爱奥尼亚人、多利安人和伊奥尼亚人。叙拉古住着多利安人，稍北的卡塔尼亚住着爱奥尼亚人；一水之隔的亚平宁半岛最南端住着伊奥尼亚人（泰勒斯被认为是伊奥尼亚学派的创建人），稍北的毕达哥拉斯学园所在地塔兰托则住着迈锡尼人，他们说着不同的方言。

多利安人最早出现在荷马史诗《奥德赛》中，他们生活在克里特岛上。追根溯源，多利安人可能来自巴尔干岛北部，后迁移到伯罗奔尼撒半岛、罗德岛、克里特岛和西西里岛东部地区。叙拉古的多利安人多是从科林斯移民来的，那是在伯罗奔尼撒半岛与希腊本土的接壤处。

沉思的阿基米德。意大利画家费蒂作于1620年。

大约在阿基米德出生前一个世纪，叙拉古人建立起一个帝国，他们向北把势力扩大到意大利南部，向南与迦太基（今北非突尼斯）人进行了三次战争，后者是地中海东岸的腓尼基人建立起来的。但在阿基米德出生前两年，叙拉古帝国突然瓦解。

在阿基米德生活的年代，古希腊的鼎盛时期已经过去，经济、文化中心转移到埃及北部的地中海港市亚历山大；与此同时，亚平宁半岛上新兴的罗马帝国，正不断地扩张势力。阿基米德生长在这一新旧交替的时代，而叙拉古城也成为多种势力的角力场所。

阿基米德出身贵族，他的父亲菲迪亚斯是一位天文学家，与早些时候的那位大雕刻家、画家、建筑师同名，却没有亲戚关系，后者曾参与雅典卫城上的巴特农神庙建设。有人因此推断他的爷爷是艺术家，或者至少是艺术爱好者。

可以确认的是，阿基米德从小受父亲影响，喜欢思考和研究。大约在十岁左右，父亲送他到埃及的亚历山大念书，那是当时西方世界的学术中心，有一座著名的大学和图书馆。学者云集，数学、天文学、医学研究较为发达，阿基米德跟随包括欧几里得门徒在内的专家学习，打下了日后从事科学研究的基础。据说他在亚历山大发明了螺旋泵——一种提水的装置，曾被埃及人广泛使用。

02 亚历山大

阿基米德在亚历山大求学的经历我们不甚了解，其时赫赫有名的大数学家欧几里得很可能已不在人世，至少离开教学岗位了。因为欧几里得虽然生卒年和出生地不详，但他的执教应大体在托勒密一世统治时期（约公元前323-前285）。在亚历山大期间，阿基米德至少结交了三位同窗或好友，科农（Conon）、多西修斯（Dositheus）和厄拉托色尼（Eratosthenes）。

科农是萨摩斯人，与他的前辈老乡毕达哥拉斯一样，也是一位数学家和天文学家。科农是阿基米德最要好、最信得过的朋友，两人的友谊维持了一生，他后来成为托勒密三世的宫廷天文官。科伦在圆锥曲线方面的工作，成为阿波罗尼奥斯（Apollonius）《圆锥曲线论》第四卷的基础。

厄拉托色尼是北非昔兰尼加（今利比亚拜尔盖）人，他比阿基米德小十来岁，却有着“柏拉图第二”的雅号，后来担任亚历山大图书馆馆长，平素非常讲究穿戴，八十岁时因为双目失明绝食身亡。

厄氏多才多艺，写过十卷本的古代戏剧史，是一位五项全能运动员，他在数学方面创立了筛法，这个方法及其推广如今在数论领域仍十分有用。他测出了地球的周长，与准确的数字只差两百公里；还根据大西洋和印度洋的潮涨潮落情况，推断它们是相通的，15世纪的葡萄牙探险家达·伽马依据此理论从水路到达印度。他还利用极圈和回归线划分出地球的五个气候带，沿用至今。

返回故乡叙拉古以后，阿基米德与科农、厄拉托色尼保持通信，他把《抛物线求积》、《论螺线》、《球柱和圆柱体》的论著寄给科伦，把《论力学定理和方法》和《群牛问题》的论著寄给厄拉托色尼，通过他们也转达给了亚历山大的同行，而两位朋友也把自己的工作告诉阿基米德。

残留在古建筑上的图案，作者摄于西西里。

据4世纪的数学家帕波斯（Pappus）所言，著名的阿基米德螺线是科农发现的，现今巴黎二十个区便是依此曲线排列，这个图案还出现在2004年雅典奥运会的闭幕式上。可惜，科农本人的著作均已遗失，包括7卷本的《论天文学》和《答色腊西达库斯》，后者讨论了圆锥曲线和圆的交点问题。

科农去世以后，阿基米德又与科农的学生、研究历法和天气预报的犹太人多西修斯通信，他在信中写道，“听说科农已经死了，他是我非常好的朋友，而你与他十分相熟，又是学习几何的学生……因此我写信给你，寄给你一些几何定理，因为我已经习惯写信告诉科农了。”

从阿基米德其他著作的前言中我们得知，多西修斯在给阿基米德的信中，也经常问起一些数学问题，至于具体内容是什么，无人知晓。无论如何，阿基米德的主要学术成果，均是在与这些亚历山大学者的通信中为人所知并保存下来的。

究其原因，古希腊没有学术刊物，出版书籍也非易事，因此许多学者通过给朋友们写信，向世人宣布自己的学术成果，附信的内容也成为论著的序言。比阿基米德稍晚的阿波罗尼奥斯也是这样做的，他与欧几里得、阿基米德并称为亚历山大黄金时期的三大数学家。

阿波罗尼奥斯年轻时也在亚历山大求学，后来到过小亚细亚米利都北面的帕加马王国，那里有一个大图书馆，规模仅次于亚历山大。他在帕加马认识欧德莫斯（Eudemus）和阿塔罗斯（Attalus），回到亚历山大后，把他的名著《圆锥曲线论》前3卷和后5卷分别寄给欧德莫斯和阿塔罗斯，两人因此在数学史上留名。但此欧德莫斯非数学史家欧德莫斯，后者来自罗德岛，是亚里士多德的学生。

03 力学之父

阿基米德是叙拉古统治者希罗王的亲戚，和王子格伦是朋友，格伦后来继承了王位。公元前1世纪的罗马建筑师、作家维特鲁威在其十卷本的名著《建筑学》第九卷中，记叙了阿基米德和希罗王一则千古传诵的故事。

随着希罗王的政治威望和权势的日益提高，他决定建造一个华贵的神龛，内装一个纯金的王冠（wreath，其实是环状花冠），以报答神灵的恩泽。金匠如期完成了任务，本应得到奖赏，偏偏这时候有人告状，说他偷去一部分金子，代之以银子。国王甚为愤怒，却又无法判断真假，便请聪明能干的阿基米德来鉴定。

起初，阿基米德也想不出好办法。苦闷之际，他到公共浴室洗澡，当浸入放满水的木桶时，一部分水溢出桶外，他的身体顿觉轻飘，于是豁然开朗。阿基米德领悟到，不同质料的物体，虽然重量相同，但因为体积不同，排出的水量也必不相同。根据这一道理，不仅可以判断王冠是否掺假，还可以知道少去的黄金份量。

阿基米德从浴盆里站了起来。

阿基米德高兴地跳了起来，赤身裸体地用多利安方言高喊“尤里卡！”意思是，“我找到了！”他不仅揭穿了金匠的劣迹，且将其上升到理论高度，得到流体静力学的浮力原理：物体在流体中减轻的重量，等于排去流体的重量。

这个原理记载在阿基米德的著作《论浮体》中，《建筑学》因为这则故事被数学家们知晓，文艺复兴以后它成为古典时期的建筑名著。另有作者记成是希罗王头上的王冠，如同专家所分析的，这不甚合理，如此轻巧的体积恐不能混入银子，也难以用排水法鉴别真伪。

1500年以后，意大利画家达·芬奇依据《建筑学》第3卷中提出的人体比例要求和黄金分割律，绘出了钢笔素描《维特鲁威人》，后来成为艺术史上最著名的素描，《建筑学》也借此进入了绘画史。其实，维特鲁威本姓波利奥，因为与同时代的诗人、演说家兼历史学家同名，故被后世写成维特鲁威。

在帕波斯的著作《数学汇编》里，记载了阿基米德另外一个有名的杠杆定律的故事。这个定律说的是，如果两个物体与一个支点的距离反比于其重量，则杠杆获得平衡。杠杆定律奠定了力学的基础，阿基米德因此发出豪言壮语：“给我一个支点，我可以移动地球。”（希腊语原文：Δός μοι πᾷ στῶ καὶ τὰν γᾶν κινήσω. 英译：Give me a standing place and I will move the earth.）

其实，准确的说法是，“如果另外有一个地球，就可以站在那儿移动这一个。”这是1世纪罗马帝国时代的希腊传记作家普鲁塔克在《马塞勒斯传》里描写的，阿基米德还向希罗王夸下海口：任何重物都可以用一个给定的力来移动。国王听后大为惊讶，要求阿基米德用事实来证明。

于是阿基米德从国王的船队中选了一艘有三根桅杆的货船，那通常需要很多人花大力气才拖得动。阿基米德安装了一组滑轮，一个人独自握着绳子站在远处，轻而易举地将船拉了过来。而依据5世纪的拜占庭哲学家普罗克洛斯（Procrus）的说法，那是希罗王为托勒密王建造的一艘大船，下水时几乎动用了所有的叙拉古人，而阿基米德凭借自己发明的机械装置，使得国王一个人就把它拖动。

尼加拉瓜邮票上的阿基米德和杠杆原理。

国王因此对他佩服得五体投地，并当众宣布，“从现在起，阿基米德说的话我们都要相信。”有趣的是，笔者发现，今天通过巴拿马运河或苏伊士运河上的每一艘巨轮，依然依靠轨道上的滑轮车牵引。

04 数学之神

阿基米德不仅出身高贵，内心也具有贵族气质，他对自己的实用发明并不十分看重，这从他流传下来的著作可以看出，那几乎是清一色的数学问题，而机械方面的发明全仰仗他人的记载，但他对机械学的兴趣还是深深地影响了他的数学思想。

《论球与圆柱》可能是阿基米德最得意的数学著作，序言是他给多西修斯的一封信。书中给出了六个定义和五个公理，例如：两点之间的所有连线，以直线最短；以相同的平面曲线为边界的曲面中，以平面的面积最小。最著名的公理也叫阿基米德公理，用现代数学语言来描述就是：任给两个正数a和b，必存在自然数n，使得na > b。从这些定义和公理出发，阿基米德推导出了六十个命题。

例如，阿基米德发现并证明了，球面积等于它的大圆面积的4倍，球体积等于以它的大圆为底、半径为高的圆锥体积的四倍。后者意味着：以球的大圆为底、直径为高的圆柱的体积是球体积的二分之三。实际上，这便是著名的球体积公式：

这属于命题34，那也是应他要求刻在自己墓碑上的著名论断。七百年以后，利用3世纪数学家刘徽提出的牟合方盖思想，中国晋朝的数学家祖冲之、祖暅父子也得到了同一结果。

镶嵌在圆锥里的球，阿基米德墓的标志。

又如，命题14说的是，正圆锥体的侧面积等于以底面半径与母线的比例中项为半径的圆的面积。实际上，这就等于圆周率、半径和母线三者的乘积。但在古希腊，由于毕达哥拉斯学派发现了

的无理性，引发了第一次数学危机，线段的长度是否存在成了问题。

虽说二个世纪以后，欧多克斯（Eudoxus）通过引进不可通约概念，将这一危机化解。不过，数学家仍避免线段的长度概念，这就是为何阿基米德选择用矩形的面积来表达。从阿基米德公理出发，他用穷竭法（method of exhaustion）严格地证明了欧几里得《几何原本》中的一条定理：只要边数足够多，圆外切正多边形的面积与内接正多边形的面积之差可以任意小。

所谓穷竭法是公元前5世纪的雅典演说家、政治家安提芬（Antiphon） 创立的，他在研究“化圆为方”问题时，提出了使用圆内接正多边形面积“穷竭”圆面积的思想。稍后，欧多克斯加以改进，将其定义为：“在一个量中减去比其一半还大的量，不断重复这个过程，可以使剩下的量变得任意小”。

希腊邮票上的阿基米德。

阿基米德进一步完善了穷竭法，并将其广泛应用于求解曲面面积和旋转体体积。例如，他通过把[0,1]区间n等分，累加矩形条面积，算出了

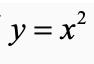
和x轴在该区间上曲边三角形的面积。遗憾的是，用穷竭法计算不同的曲边形面积时，需要采用不同的直边形去逼近，计算过程采用了特殊的技巧，因而不具有一般性，无法推广到一般的曲边梯形。

《圆的测量》是一本内容较薄的著作，只有三个命题，均是有关圆的面积和圆周率的，却同样不可小觑。虽说欧几里得在《几何原本》里讨论了许多圆的性质，却压根没提圆周率的值和圆面积、圆周长的计算公式。

阿基米德弥补了这一不足，其中命题1是这样叙述的：圆的面积等于一个以其周长和半径作两个直角边的直角三角形的面积。简单的说就是：圆的面积等于半径乘半周长。这与中国数学古籍《九章算术》里的说法“半周长半径相乘得积步”，或者公元263年刘徽注释的说法“半周乘半径为圆幂”，是等价的。

命题3给出了圆的周长与直径之（0圆周率）的上下界，即：

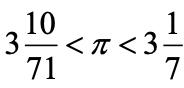
阿基米德用他的穷竭法，分别计算出了内接和外切正96边形的周长。这也是科学史上首次用上、下界来确定一个量的近似值，同时提供了误差估计。值得一提的是，不等式左右两端都是连分数的渐近形式，换句话说，在不超过7或71的所有分数中，它们是最接近于圆周率值的。阿基米德得到的圆周率是3.14，精确到小数点后两位，这是公元前人类所得到了最精确的结果。在此之前，最好的结果是古埃及人的3.1，而古巴比伦人和后来的《九章算术》给出的结果都是3.0。

在《论锥形体和球形体》中，阿基米德研究了椭圆的面积以及旋转体的体积，进一步深化了穷竭法，十分接近今天的积分法思想。而在《论螺线》一书中，他研究了螺线与出发点的垂线围成的曲线面积，以及螺线的切线，后者用到的微分学的思想。

所谓螺线，是指沿绕一定点匀速旋转的直线作匀速运动的点的轨迹，用牛顿发明的极坐标表示就是r=aθ。如同20世纪的美国数学史家E·T·贝尔所言，他（阿基米德）比牛顿和莱布尼兹领先两千多年发明了积分学，在他的一个问题（指螺线）中，领先他们发明了微分学。难怪1世纪的罗马博物学家、《自然史》作者普林尼要赞颂阿基米德是“数学之神”。

阿基米德也留传下一部算术著作《沙粒的计算》，这唯一的一部算术著作也可能是他的最后一部著作。这是他为外行人写的一些“机智的妙语”，充满了想象力，他把书献给希罗王的儿子格伦，堪称世界上最早的科普著作。

意大利邮票上的阿基米德。

全书只有一个定理，即相当于现今的指数乘法法则。阿基米德先给出了地球、月亮和太阳的大小估计，进而计算出沙粒的数目。不过，如同他事先所说的，这只是一种假设，这些数字与实际出入较大。阿基米德以万为基础，建立新的记数法，使得任何大的数都能表示出来。他算出充满太阳系的沙粒为10颗，即使是扩充到整个宇宙，也只能容纳51 10⁶³颗。

最后，我们谈谈阿基米德的数学著作对后世的影响。虽然他的工作很有独创性，比如计算球的表面积和体积公式，用22/7作为圆周率的近似值，但在古代的影响十分有限。他的工作也没有被继承和发扬，没有人试图推广他的旋转体体积公式，即使在8世纪和9世纪他的著作被译成阿拉伯文之后。

随着文艺复兴的到来，包括布鲁内莱斯基（佛罗伦萨大教堂的设计者）和达芬奇这样的巨匠都对阿基米德入迷，前者还有“阿基米德第二”的雅号，但他们看的都是手抄本。1544年，阿基米德的7部希腊文著作在巴塞尔首次印刷，附有拉丁文译文，它们在当时第一流的数学家和物理学家，包括开普勒和伽利略的著作中有所反映。对17世纪的笛卡尔和费尔马，更是产生了巨大的影响。不幸的是，他的《方法论》直到20世纪初才被发现。

05 羊皮书稿

1906年，丹麦文献学家海伯格（Heiberg，1854-1928）在君士坦丁堡发现了阿基米德寄给厄拉托色尼的那篇论著《论力学定理和方法》（以下简称《方法论》的羊皮书），此前它被认为已经遗失了，且连阿拉伯文版和拉丁文版也不存在。两年以后，海伯格再次去君士坦丁堡，经过不懈的努力，终于使185页的文字重见天日（除去少数完全看不清）。

在这篇论文中，阿基米德解释了他怎样通过在想象中比较一个已知面积或体积的图形和立体，以及一个未知的图形和立体，从中得到了他要寻求的事实；而一旦知道了事实，那么在数学上证明它就比较容易了。这有点像如今的数论学家，利用想象力和计算机寻找数的规律，再设法证明它；不同的是，这种证明通常很不容易。

在《方法论》中，阿基米德阐明了平衡法。穷竭法主要用来证明结论，却不易发现新的结果。阿基米德用平衡法计算物体的面积或体积，也是依据德谟克利特的原子论思想，先把面积或体积分成许多窄的平行条或薄的平行层。进而阿基米德假设把这些薄片挂在杠杆的一端，使它们平衡于容积和重心都已知的一个图形，而且已知图形的面（体）积一般都是容易求得的。

例如，求球体积时，他把同一个球、圆柱和圆锥放在一起，把球和圆锥的薄片挂在杠杆的一侧，而让圆柱的薄片挂在另一头，利用力矩和杠杆原理，以及圆柱和圆锥的体积公式，推导出了球体积公式。

看得出来，除了微积分或无穷数学的思想，阿基米德研究数学的第二个武器是力学和物理学。我们再举两个例子，一个是重心。牛顿力学里，假设每个星球都是单个的点，这样的点叫重心。圆的重心便是圆心，正方形或平行四边形的重心是对角线的交点。而对于三角形，阿基米德证明了，重心就在任意一条中线距离边长的的三分之一处。这个结论是《论平面平衡》的命题1。再来看抛物线，这似乎是数学家发明的游戏工具。然而，现代科学却表明，围绕着原子核的电子、发射到太空的火箭、投石机弹出的石子，它们的运动轨迹均为圆锥曲线。

下面我们来讲述阿基米德羊皮书的历史。羊皮书是由羊皮纸（perchment）做成的，得名于它的诞生地，就是前面提到的帕加马王国（Pargamon）。当年那儿建立了大图书馆和大学，成为希腊散文和修辞的中心，并试图与亚历山大竞争文化学术中心地位。

托勒密王朝为了阻碍这一竞争，严禁向帕加马输出纸莎草纸，于是帕加马人在公元前2世纪发明了羊皮纸。羊皮纸由小羊皮或小牛皮制作，经石灰处理，剪去羊毛，再用浮石软化。这样的纸两面光滑，书写方便，尤其适合鹅毛笔，摺成书本也没问题。比纸莎草纸更适用，但价格昂贵。从公元前2世纪起，羊皮纸与纸莎草纸同时被使用。公元3到13世纪，欧洲各国普遍使用羊皮纸书写文件。14世纪起，逐渐被中国的纸取代。

公元330年，第一个基督教皇帝君士坦丁大帝在博斯布鲁斯海峡建造了一座城市，那便是东罗马帝国的首都君士坦丁堡。他下令抄写50本《圣经》，稍后批准了一项保护古典文献的计划，于是抄录员成了一份可靠的职业。3个世纪以后，圣索菲亚教堂落成，这座宏伟壮丽的建筑物被认为是图形和数字的呈现，是两位小亚细亚建筑师安提缪斯（Anthemius）和伊西多尔（Isidore）设计的。

此两人是阿基米德的崇拜者兼论著编辑，同时代的数学家欧多修斯（Eutocius）加以注释使之更为著名。可以想象，那时的君士坦丁堡拥有各种阿基米德著作。其中9世纪的一位牧首（教皇）佛提乌斯（Photius）通晓希腊古典文献，他收集编辑出版了自己读过的所有著作，冠名以丛书，并发明了书评。他还派遣学生西里尔兄弟去斯拉夫人中间传教，导致他们发明了西里尔字母，至今仍为俄罗斯、乌克兰、白俄罗斯和巴尔干半岛等十多个国家的语言使用。

君士坦丁堡牧首佛提乌斯是一位爱书人。

9世纪中叶，抄写的方式从大写字母改为草书小写，这样一来速度加快，且每页文字内容增多。9世纪下半叶，叙利亚数学家、天文学家塔比特（Thabit ibn Qurra）在巴格达的智慧宫里，将阿基米德的著作从希腊文翻译成阿拉伯文。在12世纪时，又被意大利人吉拉尔德（Gerard）在托莱多译成拉丁文。那以后，君士坦丁堡在1204年经历了一场空前的灾难，东征的基督教十字军洗劫了这座欧洲最富有的城市。

阿基米德的著作只留下三个羊皮书抄本，分别称为A、B、C。三个抄本都包含《论平面平衡》，A和B都包含《抛物线求积》，A和C都包含《球体和圆柱体》、《圆的测量》和《论螺线》，B和C都包含《论浮体》；A是《锥形体和椭球体》、《沙粒的计数》的唯一抄本，C是《方法论》和《十四巧板》的唯一抄本。当然，还有著作不在任何抄本之列，有的已经遗失，有的如几何题集《引理集》，因有阿拉伯文版流传下来。

阿基米德羊皮书《十四巧板》封面插图。

如今，A和B已经不复存在，只有它们的复本和译本留下来，但它们已经完成了自己的使命，把阿基米德的论著和思想传递到了近代。如此说来，海伯格当年发现的抄本C不仅是含有《方法论》和《十四巧板》（此书表明阿基米德已经掌握了组合学）以及希腊文《论浮体》的孤本，也是幸存下来的最古老的阿基米德论著的希腊文手稿。

这部羊皮书上阿基米德的著作抄于10世纪，后来被人擦掉，大约在13世纪时写上一大堆东正教的祈祷文和礼拜仪式，作为中世纪的宗教文献在一座修道院保存下来。旧的字迹隐约可见，海伯格惊喜地发现，那是阿基米德的著作。他的著作虽然不像《几何原本》那样浑然一体，但也所言有据、论证严密。

20世纪20年代，一位曾在希腊服役的法国人斯里克斯在游历土耳其时得到这本羊皮书，把它带回了巴黎。1947年，他搬到法国南方，把公寓连同羊皮书送给了女儿安妮。最晚在1970年，安妮知道这本书的价值，于是准备私下出售。但是，直到1998年10月29日，纽约克里斯蒂拍卖行的锤音落下，这部羊皮书才以两百万美元被一位不愿透露姓名的美国富翁买下，如今收藏在巴尔的摩华尔特艺术博物馆。

经过考古学团队（含科学史、数学史、艺术史、古籍手稿、化学、数码成像和X射线成像等方面专家）多年的合作研究，这部遗著终于与大家见面了。阿基米德在书中证明了，抛物线形（被一条与准线平行的直线所截的图像）与其内接三角形的面积之比为4比3（如图）。这一点再次证明了毕达哥拉斯学派揭示的整数比例关系无所不在，在《方法论》中，几乎每个命题都如此神奇。

06 英雄挽歌

公元前212年，中国的皇帝秦始皇下令在咸阳焚书坑儒，460多名儒生惨遭杀害。那一年，叙拉古的阿基米德也走到了生命的尽头。

原来，出于商业、交通和殖民利益等的冲突，从公元前264年到前146年，迦太基与罗马帝国之间发生了三场战争，史称布匿战争，因为罗马人称迦太基人为腓尼（Peoni），转为布匿（Punic）。

其中尤以第二次布匿战争最为惨烈，那是在公元前218年到前201年间，犹如20世纪的第二次世界大战。迦太基人一度占据了上风，尤其在青年统帅汉尼拔的领导下，在海上完全取得了控制权，他率领的军队从陆地越过比利牛斯山和阿尔卑斯山，进入到亚平宁的腹地，最后因罗马人突袭迦太基本土，回军驰援而功亏一篑。

叙拉古的阿基米德广场。

由于叙拉古与迦太基结成同盟，且叙拉古又在罗马船舰征战迦太基的途中，不可避免地成为罗马人攻占的目标。公元前214年，罗马名将马塞勒斯（Marcellus）率领大军围攻叙拉古。许多史书记载了这场战争，最早的是公元前2世纪的希腊政治家、历史学家波利比奥斯（Polybius）的《通史》。

书中写道，马塞勒斯从海上发起攻击，叙拉古人依靠阿基米德发明的起重机之类的器械将靠近岸边的船只抓起来，再狠狠地摔下去。马塞勒斯用八艘五层的橹船推进，每两艘连锁在一起，可是叙拉古人未等靠近，就用强大的机械把巨石抛出，形同暴雨，罗马兵死伤无数，只得后退。

还有一种传说见于2世纪希腊修辞学家、讽刺作家卢西恩（Lucian）的记载，说阿基米德用一面巨镜反射阳光来焚烧敌船。这或许是夸大的说法，不过至少可以说明，当时阿基米德已经发现抛物面反射镜能够聚焦的性质。后来，罗马人又采取夜袭的方法，谁知阿基米德早有防备，事先制造了一种叫“蝎子”的弩炮，专门对付近处的敌人，罗马兵又一次吃了大亏。最后，马塞勒斯干脆放弃正面围攻，而采用长期围困的策略。叙拉古终于因为粮食耗尽陷落，公元前212年，在一个庆祝的节日夜间被罗马人悄悄攻占，阿基米德也光荣牺牲。

关于阿基米德之死，最早的说法出自公元前后的历史学家、《罗马史》作者李维（Livy），“在兵荒马乱之中，侵略军大肆杀戮，阿基米德面对地上的一幅沙图思考，一个罗马士兵将他刺死，根本不知道他是谁。”策策斯教诲诗中是这样描写的，阿基米德没有注意到逼近他的人是谁，“喂！站远一点，别动我的图。”结果他被杀害了。而传记作家普鲁塔克的说法是，阿基米德要求让他先找到问题的答案，结果激怒了士兵。有意思的是，这则阿基米德的典故可能是唯一有关纯粹数学的。

据说，阿基米德被杀死后，马塞留斯非常悲痛，他严肃处理了那个士兵，还寻找到阿基米德的亲属，给予抚恤并表达敬意，又给阿基米德立碑，聊表敬仰之请。并让人在墓碑上刻上球内切于圆柱的图案，以资纪念。

值得一提的是，普鲁塔克是在《马塞勒斯传》写到这则故事的，他并没有为阿基米德立传，也许他认为，那位将军比阿基米德更重要。结果呢，将军本人因为这则有关阿基米德的记载才被人们记忆。一个多世纪以后，古罗马的政治家、作家西塞罗担任西西里的税务官，有意去墓地凭吊，结果无人愿意带路，他只好自己拨开荆刺寻找到了，只见那球和圆柱的图案仍历历在目。只是我不得而知，在墓碑上刻印图像或公式的传统，是否源于阿基米德。

英国哲学家怀特海曾经说过，“欧洲哲学传统最可靠的一般特征在于，它是由对柏拉图的一系列脚注组构成的。”有人借此比喻，“欧洲科学传统最可靠的一般特征在于，它是由对阿基米德的一系列脚注构成的。”

如今阿基米德已被公认为是古代世界最伟大的数学家、科学家。贝尔称：任何一张列举有史以来最伟大数学家的名单中，必定会包括阿基米德，另外两个通常是牛顿和高斯。不过，若拿他们的丰功伟绩与其所处的时代来比较，仍应首推阿基米德。甚至于菲尔兹奖章上刻着的也是阿基米德像，这与诺贝尔奖章刻着捐助人的像形成对照。

菲尔兹奖章，刻着阿基米德肖像。

1979年，阿基米德的同胞诗人、克里特岛出生的埃利蒂斯获得了诺贝尔文学奖。在一首冠名《英雄挽歌》的长诗中他这样写道，“梦的轻烟是如何上升的……/ 这一顷刻将另一顷刻抛弃 / 永恒的太阳就这样离开了世界”。

2013年夏天，杭州彩云居

“

作者简介

蔡天新

浙江大学数学学院教授、博士生导师、求是特聘学者，近作有《小回忆》增订版、《我的大学》（修订版）、《26城记》、《数学与艺术》、《经典数论的现代导引》（中、英文版）、《完美数与契波那契序列》（即出），主编《地铁之诗》、《高铁之诗》。

”

制版编辑 | Morgan

,