双因素方差例题（15双因素方差分析）

管理困惑: 结果主要是由哪个因素所致？

在管理工作过程中，管理者常常被下列问题所困惑：

同一个市不同区销售不同品牌的手机，受手机品牌因素影响和销售区域因素影响，手机销量不同。市场经理想知道，手机品牌和销售区域对手机销售量差异的影响到底哪个影响因素更大一些？

又如，用不同的机器加工制造相同的零件，在加工过程中，对每一个机器使用不同的冷却剂。经过检测，发现零件直径有差异。负责生产和技术的经理需要分析确定所加工零件的直径差异是加工设备造成的还是由冷却剂使用不同造成的？不同类型的冷却剂，对加工零件的直径是否有显著差异？

再如，R自带数据集中在研究维生素C对于豚鼠牙齿生长的影响。豚鼠牙齿生长主要因为给药方式不同还是剂量的使用不同造成？......

要科学可靠的回答此类问题，就需要使用“双因素方差分析”。这也正是本文要讲解的内容。

在之前的文章里，我讲解过“单因素方差分析（One-Way anova）”，如果您对方差分析没有初步的认识的话，请您先通过查阅我公众号往期文章，先行学习”单因素方差分析”。

"单因素方差分析（One-Way ANOVA）"

什么是双因素方差分析？

双因素方差分析是一种统计分析方法，它可以用来分析两个因素的不同水平对研究对象测量结果是否有显著影响，以及两因素之间是否存在交互影响效应。

因素：影响研究对象的某一指标、变量、响应、测量值等。

水平：因素变化的各种状态或因素变化所分的等级、组别或种类。

实验设计: 均衡实验与非均衡实验

通常，在使用双因素方差分析前，要先对两个因素的不同水平的组合进行试验设计。要求每个因素水平组合下所得到的样本的含量是相同的，这就是均衡实验。如果样本含量不全一样，那么就是非均衡实验。

对两个因素的不同水平下的每一个组合，如果只做一次实验测量，用这样的数据来进行的双因素方差分析就为双因素无重复测量方差分析。

如果要检验两个因素的交互作用，那么两个因素的每一个水平组合至少要进行两次实验测量。如下图，行为A因素，有两个水平，列为B因素，有两个水平。对两个因素的每个水平组合做两次实验：

如果知道因素之间不存在交互作用，或者事前通过定性分析知道，因素之间虽然有交互作用但是作用很小，对实验测量结果影响很小，则可以不考虑交互作用。

模型及计算

双因素方差分析是线性模型的一种特殊情况。模型的形式为：

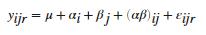
其中：

Yijr是对响应变量的观测值；

i表示行因子A的第i组，i = 1,2，…,I;j表示列因子B的j组，j = 1,2，…, J;R表示重复测量次数，R = 1,2，…, R。

据此，总共有N = I*J*R的观测值。

μ是总平均值。αi是行因子A定义的组与总均值μ的偏差。αi的值和为0。

βj是列因子B定义的组与总平均μ的偏差。βj的值和为0。

αβij为相互作用。αβij的每一行和每一列的值和为0。

εijr为随机扰动。假设它们是独立的，正态分布的，并且有常数方差。

• 关于行因子A组的均值相等的假设为：

• 关于列因子B组的均值相等的假设为：

• 关于列因子和行因子相互作用的假设为：

方差分析将总平方和(SST)分解为行因子A平方和(SSA)、列因子B平方和(SSB)、A与B相互作用平方和(SSAB)、误差平方和(SSE)。它们之间的量化关系为：

方差分析采用由因素或交互作用而产生的变异与由误差而产生的变异进行比较。

如果分子两个变量的比例高，则该因子或交互效应的影响在统计上是显著的。您可以使用F分布统计量来测量统计显著性。

• 对于行因子A的组均值相等的零假设，检验统计量是：

• 对于列因子B各组的均值相等的零假设，检验统计量是：

• 对于列因子和行因子的交互作用为零的零假设，检验统计量是：

如果F统计量的p值小于显著性水平，则方差分析拒绝零假设。最常见的显著性水平为0.01和0.05。

有关双因素方差分析的数学模型大概就介绍这些，更加详尽地讲解请查阅网络或者概率论与数理统计方面的书籍。供您参考的方差分析表如下：

案例: Two-Way ANOVA using Python

用五种不同的机器加工制造相同的零件，在加工过程中，对每一个机器使用不同的冷却剂。现在我们想知道，所加工零件的直径差异主要是由于什么原因导致的？不同类型的冷却剂，对加工零件的直径是否有差异？

读入案例分析数据：

import pandas as pd import statsmodels.api as sm from statsmodels.formula.api import ols from statsmodels.stats.anova import anova_lm from statsmodels.graphics.factorplots import interaction_plot import matplotlib.pyplot as plt from scipy import stats import seaborn as sns from statsmodels.stats.multicomp import pairwise_tukeyhsd datafile = "Two-Way Crossed ANOVA.xlsx" df = pd.read_excel(datafile) df.info() df.tail(5)

ax = sns.pointplot(x='machine', y='diameter', hue='coolant', data=df)

sns.boxplot(x='machine',y='diameter',data=df,hue='coolant')

interaction_plot(x= df.machine, trace= df.coolant, response=df.diameter,markers=['D','^'],colors=['red','blue'],func=np.mean, ms=8)

从上面的数据图可以初步判断不同加工设备不同冷却剂下零件直径均值是有差异的。为了进一步寻找显著差异，就需要做方差分析。

首先，不考虑因素之间的交互影响作用。

formula = 'diameter ~ coolant machine ' model = ols(formula, df).fit() anova_table = anova_lm(model)

在不考虑交互作用情况下，由该方差分析表可知：

“coolant”对生产出的零件直径没有显著影响。

“machine”对生产出的零件直径有显著影响。

其次，考虑因素之间的交互影响作用。

formula = 'diameter ~ coolant machine coolant*machine' model = ols(formula, df).fit() anova_table = anova_lm(model) anova_table

在考虑交互作用情况下，由该方差分析表可知：

“coolant”对生产出的零件直径没有显著影响。

“machine”对生产出的零件直径有显著影响。

“coolant和machine交互作用”对生产出的零件直径没有显著影响。

综上，影响零件直径的因素为机器设备因素。可以理解为与使用的冷却剂关系不大，可以不考虑其对零件直径加工的影响。

最后，检验残差是否正态。显然残差正态。

res = model.resid fig = sm.qqplot(res,fit=True,line="s",dist=stats.distributions.norm )plt.show()

多重比较：寻找显著差异。

既然机器设备因素对零件直径有显著影响，那么哪些加工机器设备加工零件的直径有显著差异？

from statsmodels.stats.multicomp import pairwise_tukeyhsd mc = pairwise_tukeyhsd(df['diameter'],df['machine']) print(mc) mc.plot_simultaneous()

,