导数几何意义及其应用（导数的物理意义及应用初步）

• 认识导数。。。

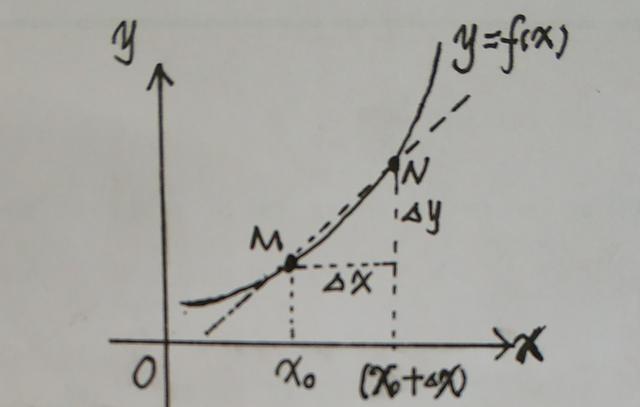
如图所示，当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限，即为函数y=f(x)在x0处的导数，记作f'(x0)或df(x0)/dx。

对应的数学表达式为：

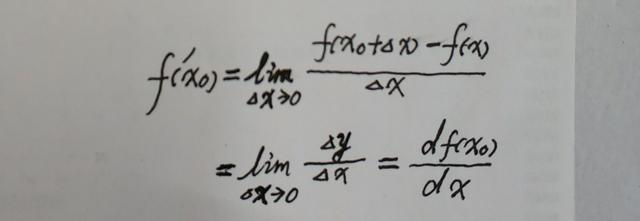
• 导数的几何意义。。。

由图可知，Δy/Δx为直线MN的斜率，当Δx趋于0时，N趋于M。所以函数y=f(x)在x0处的导数就是函数图线在x0处的斜率。

• 导数的物理意义。。。

从物理意义看，函数y=f(x)在x0处的导数就是物理量y随物理量x变化时，在x0处的变化率。

• 应用1：理解物理概念。。。

**速度v描述了物体的位置（位移）x随时间t变化的快慢，即位移随时间的变化率。

**加速度a描述了物体的速度v随时间t变化的快慢，即速度随时间的变化率。

各自对应的导数形式为：

实例分析

解答：物体的速度随时间的变化规律为：

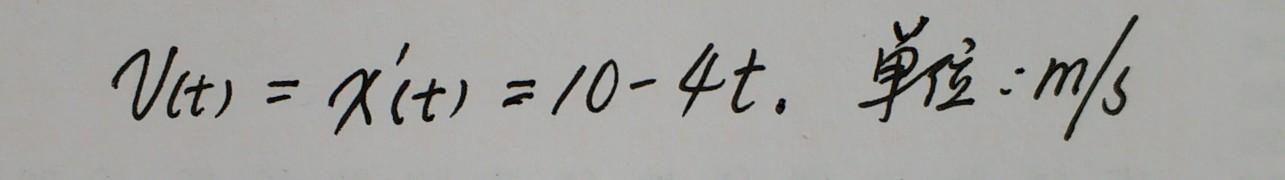
物体的加速度随时间的变化规律为：

所以物体做初速度为10m/s,加速度为4m/s2的匀减速直线运动。

• 应用2：求物理极值。。。

由导数的几何意义可知，当函数y=f(x)在x0处存在极值时，y=f(x)在x0处的导数，即函数图线在x0处的斜率为零。

实例分析

一辆汽车在十字路口等候绿灯，当绿灯亮时汽车以2m/s2的加速度开始行驶，恰在这时一辆自行车以4m/s的速度匀速驶过汽车，若二者均沿笔直的马路行驶，求：汽车在追上自行车之前两车何时相距最远？最远距离是多少？

附加：1.物理常用的导数公式

2.导数的运算法则

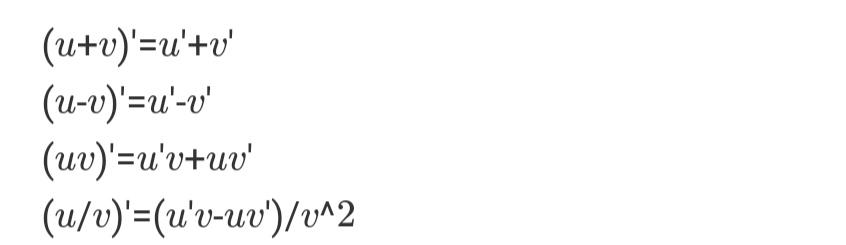
3.复合函数的导数