初三数学离点问题及答案（初中数学临界点问题与取值范围探究）

临界点和取值范围问题是中考数学常考内容之一，一般与几何、函数一起考查，而取值范围问题，可能涉及不等式和代数式有意义的问题。

我们今天简单看一下临界点问题和取值范围常考哪些内容。

（1）求取值范围：

①根据判别式求取值范围：

例：已知x²-2mx m 6=0有两个不相等的实数根，求m的取值范围

思路：显然有两个不相等的实数根需满足△=b²-4ac＞0，本式中a=1，b=-2m，c=m 6。

所以有（-2m）²-4（m 6）=4（m-3）（m 2）>0

易知 m的取值范围为m<-2或m>3

②有无数解问题：

例：❶若ax² ax 1>0恒成立，求a的取值范围。【一般不等式均有无数解，这里我们说是恒成立】

思路：实际上是考查对二次函数图像的认识，因为不等方程是＞0，所以二次函数需满足开口向上即a>0,且与x轴无交点，即判别式△<0,易知0<a<4

例：❷关于x的不等式2x 5-a>1-bx恒成立，试确定a，b的取值范围。

思路：对于任意的方程ax b=0，只有在a和b同时为0的时候，方程有无数解（为什么？因为a=0，则ax恒为0，与x的取值无关）。而对于不等式ax b>0，则必须是在a=0，b>0，时才可能恒成立。

所以此题先移项化为（2 b）x 4-a>0，则有b=-2,a<4。

②无解问题（二次函数问题不再举例）：

例：❶

思路：不等式组无解的思路是让两个不等式解到的解无公共部分例如（不存在x>1且x<0的值）。

本题中x-3（x-2）≤4，解得x≥1，第二个分式不等式解得x＜a，所以只需保证a不大于1即可，即a≤1。（注意对于a是否能取1，不熟练时单独拿出来分析一下）

❷我们将上一题略微改动：

思路：注意改动的位置，第一个不等式不等式改变，则解变为了x≤1，而整个不等式组的解也是x≤1，所以第二个不等式解到的解必须是x<b,且b需要时大于1的数。而第二个不等式移项化简后未（3a-2）x<a。所以必须有3a-2>0，且a/（3a-2）>1，解得2/3<a<1【同样，临界点a=1可以单独拿出来分析】

③代数式有意义问题（定义域）：

一般情况下初中阶段代数式有意义的问题主要是偶次（初中一般就是根号）根下代数式需大于等于0，分式中分母不等于0。

例：

显然此题即有根号又有分式需满足x-2>0,3-x≥0，则2<x≤3。

④给定x的范围求y的范围（值域）：

最简单的问题是一次函数：若y=-2x 4，且x>4，试求y的取值范围。

因为x>4,则-2x<-8,所以y=-2x 4<-8 4=-4，但对于二次函数问题则变得稍微复杂一些：

例❶：求关于x的函数y=x²-4x 9在实数范围内y的取值范围

显然可以进行配方或直接应用顶点公式，这里举例是非常简单的所以进行配方（根据（a b）²=a² 2ab b²，一对一的凑出来， 这里把x看成a，2b应该对应-4，则b=-2，b²=4）：

y=x²-4x 4 5=（x-2）² 5≥5

❷：还是上面的题目，关于x的函数y=x²-4x 9在0<x<3时y的取值范围。

有的同学非常聪明，直接将x=0和x=3，代入后y=9或y=6，所以6<y<9。

注意：这样做未考虑其他取值情况，而实际上当x=2时y取最小值5，故y的取值范围是5≤y＜9。

（2）临界问题：

一般情况下在确定某代数式的取值范围时均会考虑临界问题，以上举例中的各边界点均是临界，但在几何中和二次函数或反比例函数找交点时略有不同，常常与动点一起考查。

①几何相关

例❶：Rt△ABC中，∠BAC=90°，AB=3，AC=4，P为边BC上一动点（不包括点B、C），PE⊥AB于E，PF⊥AC于F，则EF的取值范围是？

思路：我们能看出来的是AFPE是个矩形，这样求EF其实就演变成了求AP。P点在移动过程中当AP垂直BC时最小，当移动到C点时最大。

当垂直时：5×AP=3×4，AP=12/5,而移动到C时最大为4，显而易见。

例❷：如图，在直角坐标系中，△ABC的顶点A、B、C的坐标分别是（3，3）、（2，-2）、（0，c），则当△ABC成为锐角三角形时，c的取值范围是_________________.

如图左图是给出的图形，有图我们找临界点，首先C向上移动不能超过上红线、向下移动不能超过下红线同时，移动过程中∠ACB还会经历一个从小变大再变小的过程，我们还要找到中间的临界点，这道题对于高中阶段解答起来要比初中容易的多（斜率相乘等于-1），也不是不可解。

首先距离公式推导（按下图，AD和BD均用AB坐标来表示出来，不推导出公式也可以，但要会计算d²=（x1-x2）² （y1-y2）²：

AB²=AD² BD²=1 25=26

上方临界点：（c-3）² 9 26=4 （c 2）²解得c=3.6

下方临界点：26 4 （c 2）²=（c-3）² 9解得c=-1.6

验证中间临界点：（c-3）² 9 4 （c 2）²=26解得c=2或c=-1。

则可知c点的取值范围被分成了两段-1.6到-1,2到3.6。

几何题先举例此两题

---

②函数问题

例：

这是某年北京市中考压轴题，其中第二问的第二小题便是临界问题，需要画图：

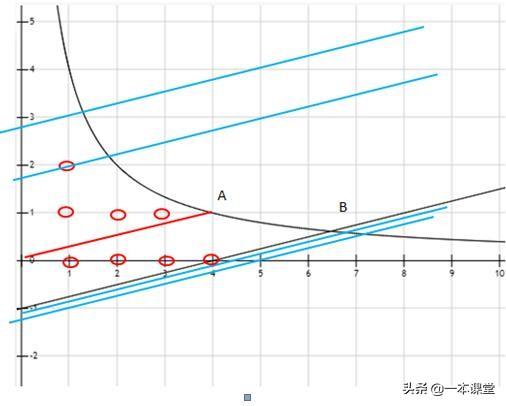
蓝线便是临界（一般解题思路是一点点的平移）

k值已计算得4，而实际上直线平移过程中与y轴的交点便是（0，b），简单理一下思路：

例：已知点A，B的坐标分别为（1，0），（2，0），若二次函数y=x² （a-3）x 3的图像与线段AB只有一个交点，则a的取值范围是（ ）。

一定要画一画：

明确一点：此二次函数开口向上：那么如果二次函数与x轴只有一个交点，那么此时

（a-3）²-12=0，解得

显然当a=3 2√3时满足题意。

另外：若另一个交点在右侧，一个在其中则有当x=2时y<0,当x=1时，y≥0，即-1≤a＜-1/2;

若另个一交点在x轴左侧，一个在其中则有当x=2时y≥0,当x=1时，y＜0，此时无解。

所以a的取值范围是a=3-2√3或-1≤a＜-1/2。

返回头再看此题实际上需满足x=1和x=2时y的取值异号或其中一个为0即可，

即求（2a 1）（a 1）≤0,且判别式大于等于。

---

关于临界点或取值范围的题目数不胜数，这里只是简单举例。题目有找的，有临时出的。

,