python量化交易自学一般要学多久（零基础强化学习量化交易笔记）

梯度上升是一种用于最大化给定奖励函数的算法。描述梯度上升的常用方法使用以下场景：假设您被蒙住眼睛并被放置在山上的某个地方。然后，你的任务是找到山的最高点。在这种情况下，您尝试最大化的“奖励函数”是您的提升。找到此最大值的一种简单方法是观察您所站立区域的坡度，然后向上移动。一步一步地遵循这些指示最终将您带到顶部！

在上山时，重要的是我们知道该地区的坡度或坡度，这样我们才能知道要朝哪个方向行驶。这只是奖励函数相对于其参数的导数。

梯度上升的另一个重要部分是 。这相当于我们在再次检查斜率之前采取的步数。步骤太多，我们可能超过峰会;步数太少，找到峰值需要太长时间。同样，高点可能导致算法偏离最大值，而低点可能导致算法花费太长时间才能完成。

现在我们已经了解了梯度上升的基础知识，让我们用它来执行一个相对简单的任务：线性回归。

让我们首先生成一些数据来执行线性回归。

import numpy as np import matplotlib.pyplot as plt plt.rcParams["figure.figsize"] = (5, 3) # (w, h) plt.rcParams["figure.dpi"] = 200 m = 100 x = 2 * np.random.rand(m) y = 5 2 * x np.random.randn(m) plt.scatter(x, y);

我们生成了 100 个点，随机放置在截距位置 5 且斜率为 2 的线周围。就这样我们有了一个基准，我们可以使用 scipy 函数找到最合适的线：

from scipy.stats import linregress slope, intercept = linregress(x, y)[:2] print(f"slope: {slope:.3f}, intercept: {intercept:.3f}")

slope: 1.897, intercept: 5.130

这些将是使用我们的梯度上升算法所优化的目标值。

下一步是定义我们的奖励函数。测量线性回归精度时常用的函数是均方误差（MSE）。MSE 是“估计值与估计值之间的平均平方差”。由于 MSE 是一个误差函数，并且我们正在寻找一个最大化的函数，因此我们将使用负 MSE 作为奖励函数，J:

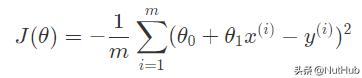
其中θ是我们的输入参数，在本例中是我们正在测试的线的截距和斜率。这个等式可以用Python表示，如下所示：

x = np.array([np.ones(m), x]).transpose() def accuracy(x, y, theta): return - 1 / m * np.sum((np.dot(x, theta) - y) ** 2)

从这里开始，我们初始化了x矩阵，其中x0=1和x1是原始的 x 值。这使得θ0 θ1​·x只需θ⋅x.

现在我们有了奖励函数，我们可以找到梯度函数，它将是J关于θ的函数:

再一次，我们可以用Python编写这个函数：

def gradient(x, y, theta): return -1 / m * x.T.dot(np.dot(x, theta) - y)

现在我们准备执行梯度上升！我们将初始化θ如[0，0]，然后使用以下命令在每个epoch或iteration中更新它：

其中α是学习率。

num_epochs = 500 learning_rate = 0.1 def train(x, y): accs = [] thetas = [] theta = np.zeros(2) for _ in range(num_epochs): # keep track of accuracy and theta over time acc = accuracy(x, y, theta) thetas.append(theta) accs.append(acc) # update theta theta = theta learning_rate * gradient(x, y, theta) return theta, thetas, accs theta, thetas, accs = train(x, y) print(f"slope: {theta[1]:.3f}, intercept: {theta[0]:.3f}")

slope: 1.899, intercept: 5.128

我们匹配了线性回归基准测试！如果我们绘制精度随时间变化的图，我们可以看到算法迅速收敛到最大精度：

plt.plot(accs) plt.xlabel('Epoch Number') plt.ylabel('Accuracy');

最后，如果我们将奖励函数投影到3D表面上并标记我们的θ0​和θ1​随着时间的推移，我们可以看到我们的梯度上升算法逐渐达到最大值：

from mpl_toolkits.mplot3d import Axes3D i = np.linspace(-10, 20, 50) j = np.linspace(-10, 20, 50) i, j = np.meshgrid(i, j) k = np.array([accuracy(x, y, th) for th in zip(np.ravel(i), np.ravel(j))]).reshape(i.shape) fig = plt.figure(figsize=(9,6)) ax = fig.gca(projection='3d') ax.plot_surface(i, j, k, alpha=0.2) ax.plot([t[0] for t in thetas], [t[1] for t in thetas], accs, marker="o", markersize=3, alpha=0.1); ax.set_xlabel(r'$\theta_0$'); ax.set_ylabel(r'$\theta_1$') ax.set_zlabel("Accuracy");

在这篇文章中，我们展示了如何使用梯度上升来最大化一个相对简单的奖励函数，只有两个参数。在下一篇文章中，我们将了解如何将奖励函数应用于交易策略，以训练算法交易模型。

相关阅读：Inv_Strategy趋势反转策略运行结果展示

点赞加关注，欢迎合作交流！

欢迎评论批评指正/提出建议！交流学习

%风险提示：本文不推荐买卖标的，仅介绍策略工具、记录程序运行结果，手工操作设置止盈止损，投资有风险，交易需谨慎，盈亏且自负。