三角形的三边关系和例题讲解（最值问题之三角形三边关系）

最值问题之三角形三边关系

【巩固练习】

1、问题情境：如图1，P是⊙0外的一点，直线PO分别交⊙0于点A、B，则PA是点P到⊙0上的点的最短距离.

（1）探究：如图2，在⊙0上任取一点C（不为点A、B重合），连接PC、OC.试证明：PA<PC.

（2）直接运用：如图3，在Rt△ABC中，∠ACB=90°，AC=BC=2，以BC为直径的半圆交AB于D，P是弧CD上的一个动点，连接AP，则AP的最小值是______________.

（4）综合应用：

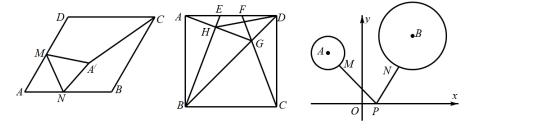
①如图5，E，F是正方形ABCD的边AD上两个动点，满足AE=DF.连接CF交BD于点G，连接BE交AG于点H. 若正方形的边长为2，则线段DH长度的最小值是__________.

②如图6，平面直角坐标系中，分别以点A（-2，3），B（3，4）为圆心，以1、2为半径作⊙A、⊙B，M、N分别是⊙A、⊙B上的动点，P为x轴上的动点，则PM PN的最小值等于________________.

,