电为什么能生磁（电和磁的那些事儿）

1.1 电生磁？

19世纪初，早在大学时期就受康德哲学思想影响的奥斯特，认为各种自然力量都来自同一根源，可以互相转化。他一直坚信电和磁之间一定有某一种关系，电可以转化为磁。而在此之前电和磁都是分开来进行研究的，例如，库伦研究了静电和静磁，并证实了二者之间不可能转化；安培和比奥等物理学家认为电和磁不会有任何联系。

1820年4月，在一次晚上的讲座中，奥斯特偶然间发现在导线通电的瞬间，其旁边的小磁针偏转了一下。这一令所有人都未引起注意的现象却让奥斯特喜出望外。之后的三个月，他又做了多次实验。并于当年7月21日，用一篇4页纸的实验报告论文：《论磁针的电流撞击实验》正式向学术界宣告发现电流的磁效应现象，即电流能像磁铁一样影响周围小磁针。

奥斯特仿佛开启了一个新纪元，物理学家们纷纷顺着这一发现进一步研究，进行定量分析。既然电流可以产生磁场，那么这个磁场长什么样呢（如何分布）？有多厉害呢（空间特定某处的磁感应强度有多大）？定性的发现某个规律之后必然要试图定量的把它描述出来，这样我不仅知道存在，还可以精确计算。

三个月之后，也就是1820年10月份，法国物理学者毕奥和萨伐尔就在拉普拉斯的帮助下找到了磁场在电流空间的分布规律：即磁场与电流的大小、方向和距离三个因素相关。具体说来，电流元Idl 在空间某点P处产生的磁感应强度 dB 的大小与电流元Idl 的大小成正比，与电流元Idl 所在处到 P点的位置矢量和电流元Idl 之间的夹角的正弦成正比， 而与电流元Idl 到P点的距离的平方成反比。公式描述即如下：

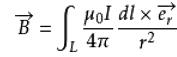
又过了两个月之后，1820年的12月，安培发现了一个更实用更简单的计算电流周围磁场的方式——安培环路定理，即在稳恒磁场中，磁感应强度B沿任何闭合路径的线积分，等于这闭合路径所包围的各个电流的代数和乘以磁导率。其数学表达式为：

此外，安培还总结了安培定则（也即右手螺旋定则）来帮助判断电流产生磁场的方向。顺便提一句，科研发现抢占先机是多么重要！

1.2 磁生电？

至此，电生磁（确切的说是电流生磁）的问题似乎研究的很透彻了。奥斯特告诉我们电流会产生磁场；毕奥和萨伐尔教我们如何计算磁场的大小；安培指导我们用更方便的方式求解磁场大小和方向。那么反过来，你一定会去想，磁能否生电呢？如果可以，分布规律又是如何？

这件事的发现是在11年之后了，也就是1831年，英国的天才实验物理学家法拉第发现了磁生电的规律，即电磁感应定律。与电生磁不同，电磁感应定律揭示静止的磁不能生电，只有变化的磁才能生电。电磁感应现象可以描述为，只要穿过闭合电路的磁通量发生变化，闭合电路中就有电流产生，所产生的电流称为感应电流。其表达公式为：

1.3 麦克斯韦方程组

至此，有关电和磁的规律我们似乎了解的足够了。但是，仔细观察后发现，安培环路定理揭示的是电流和磁之间的关系。倘若没有电流存在呢？比如，在没有导线存在的情况下，单纯的电场是否能产生磁场呢？电磁感应定律描述的是变化的磁场可以产生电场。反之，变化的电场是否也能产生磁场呢？这是安培环路定理所缺失的地方。于是，麦克斯韦就对安培环路定理进行了扩充，把变化的电场也能产生磁场这一项也加了进去，补齐了最后的短板。

至此，电和磁的统一之路就走的差不多了，麦克斯韦方程组的基本形式也呼之欲出了。我们都知道麦克斯韦方程组是由四个方程组成的，其描述了经典电磁学的一切。思考一下，如果四个方程就能描述电与磁的一切，那么分别是什么呢？下面的思路是否很自然：第一个方程描述电；第二个方程描述磁；第三个方程描述磁生电；第四个方程描述电生磁。麦克斯韦就是这样想的。