小学数学中的主要数学公式（小学数学中的4条）

　　小学数学中的4条“基本”性质

　　2018年8月7日星期二

　　拟定这样的题目，多少有些博人眼球。4条性质倒是有的，但“基本”不是。这4条性质分别是：

　　①除法的商不变性质：

人教版四年级数学上册87页

　　②小数的性质：

人教版四年级数学下册40页

　　③分数的基本性质：

人教版五年级数学下册57页

　　④比的基本性质：

人教版六年级数学上册50页

　　可见，学习最早的是“除法的商不变性质”，然后是“小数的性质”，接下来是“分数的基本性质”，最后是“比的基本性质”。亦可见，冠以“基本”的有“分数的基本性质”和“比的基本性质”。“除法的商不变性质”有时也被称为“除法的商不变规律”。

　　对于“性质”与“规律”的差别，或许您和我一样充满好奇，但相信我，您不会对此感兴趣的，它们二者的差别涉及到了哲学上的概念范畴，看了会更加糊涂，不如不看，“揣着糊涂装明白”！比如：

　　“马哲中的规律：亦称法则。客观事物发展过程中的本质联系，具有普遍性的形式。规律和本质是同等程度的概念。客观性规律：它是客观的，既不能创造，也不能消灭；不管人们承认不承认，规律总是以其铁的必然性起着作用。规律等同于真理：这个世界任何物质都受规律约束，彼此对立又互相联系统一。”

　　“性质是从客观角度认知事物的形式，是人或事物的本质。”

　　……

　　怎么样？我是成功地“糊涂”了……只是约略发现痕迹：“规律”、“法则”、“本质”、“真理”、“性质”……这些词语在某些情况下是同义的、通用的，所谓“同义相训”是也。

　　至于“基本”，倒是可以说道说道。基本指基础的、主要的、根本的。想来除此之外，还有其他的性质。我颇费周章，搜到的有：

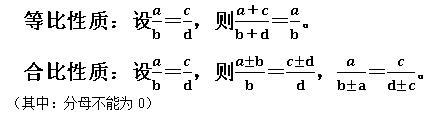
　　这些性质在初中才会学习，如果注意其假设条件就会发现：它们的出发点是“分数或比的基本性质”。由此可见，所谓“基本”性质大抵是可以推导得出其他性质的，所以称呼为“基本性质”，是由其本源、基础的地位所决定的。

　　今天以此为话题，除了可以帮助小朋友们串联、巩固已学的知识外，也是基于对这些内容产生的新的思考和认识。

　　（一）4条性质在本质上是一致地，都源于“除法的商不变性质”。

　　我们经常做这样的类比：分子、比的前项相当于被除数，分母、比的后项相当于除数，分数值、比值相当于商。三条性质可以统一为：

　　除法（分数、比）的被除数（分子、前项）和除数（分母、后项）同时乘以或除以相同的数（0除外），商（分数的大小、比值）不变。

　　（重要程度★★★★）

　　小数的性质似乎采用了完全不同的表述：小数的末尾添上“0”或去掉“0”，小数的大小不变。举例就是：

　　0.1＝0.10＝0.100＝0.1000＝……

　　如此而已。

　　但如果依据小学数学教材中给出的“分母是10、100、1000……的分数可以用小数表示”，我们可以将其还原成分数形式——这句话的本意是根据十分之一、百分之一、千分之一……引入小数的计数单位和小数的表示形式，现在，我们将其反其道行之。小数的性质展现的内容变为：

　　此时，您会发现：它的本来面目就是分数的基本性质。

　　（二）每条性质的出现都有其特殊的地位和作用。

　　（1）除法的性质出现于整数除法（除数是两位数的除法）学习完成之后，目的是为即将学习的小数除法提供算理上的依据和支撑。我们都知道，要计算一道除数是小数的除法，首先要将除数转化为整数，然后按照整数除法的计算法则进行计算。这个“转化”的过程的依据就是“除法的商不变性质”，例如：

　　223.72÷3.4＝（223.72×10）÷（3.4×10）＝2237.2÷34

　　上式中的等号不是随手写上的，显然是由“除法的商不变性质”作保证的，使得针对小数除法算式所做的变化是有理有据的。

　　除了这个主要的应用，还演生了许多“副产品”，往往都是为了更好地理解“除法的商不变性质”，比如：

　　　120÷15

　　＝（120×4）÷（15×4）

　　＝480÷60

　　＝8

　　这是一种凑巧的简便计算。再如：

　　0.86÷0.4＝2.1……（ ）

　　这道题算是够“坑”的一道题，如果依据竖式除法进行正向计算，多半会得出错误的结果0.2，甚至是2。出现这个错误的原因是：应用“除法的商不变性质”时，性质本身并没有明确告诉我们“余数也不变”。事实上，余数作为被除数的一部分，是随着被除数的扩大而扩大，缩小而缩小的。在将0.86÷0.4转化为8.6÷4的过程中得到的新的余数0.2，比原来的余数扩大了10倍，所以原来的余数是0.2÷10＝0.02。这样的题，对于深入理解“除法的商不变性质”的应用特点极为有益。出题者估计也是冲着这一点来的。但反过来想，小数的除法本来就是为了“消灭余数”的，在小数除法计算的过程中戛然而止，探问余数，也真是让人惊讶于出题者的脑洞，因为本题的结果本就是有限小数，可以除尽的：

　　0.86÷0.4＝2.15

　　最好的方法莫过于用“靠谱”的方法进行验算：

　　0.86－2.1×0.4＝0.86－0.84＝0.02

　　因为：余数＝被除数－商×除数。此诚所谓“你有你的张良计，我有我的过墙梯”！

　　（2）小数的性质的作用显见的是：化简小数、统一精度。比如：

　　105.0900＝105.09 （去0）

　　32.8元＝32.80元 （添0）

　　但更深层次的是：为小数的大小比较做铺垫。我们在整数的大小比较中学到了两条比较大小的方法：

　　①数位数，比如：1000＞999；

　　②从高位到低位一位一位地往下进行同位相比，比如：998＜999。

　　自然会想将其继承、延续下来。但小数部分的数位与整数部分的数位情况有所不同：整数部分没有最高位，有最低位（个位）；小数部分有最高位（十分位），没有最低位。生搬硬套方法①的话就会出错：

　　0.3＜0.23

　　这恐怕是由于“比位数”带来的负迁移：3＜23。

　　我们来看一组数字的“华丽”变化：

　　103＝……000000103

　　0.05＝0.05000000……

　　1.2＝……0001.2000……

　　这或许会刷新您对“数位”的理解，一个三位数103，也可以看成是无穷多位数，只不过百位以上的数位上的数字都是0。而一个两位小数0.05，也可以任意地写成三位小数0.050，四位小数0.0500……或许，数位就是一个“不确定”的东西。在以前的教材中，曾引入过“有效数字”、“无效数字”的概念，现在没有了，不过，现在看来，还是有点意义。我们不会把103写成000103，是为了追求简洁，也是因为高位添加的0都是“无效数字”，去掉了也不会影响数的大小。但有时候，人们还就是需要将数字的位数统一，比如考号1～300，将1号强制写成001，这如同统一小数位数的精度一样。需要注意的是：不要将0和无效数字划等号，比如0.05的个位、十分位上的数字0就是有效数字，不能去掉。

　　当数位不再确定、不再重要时，比较大小变化为：

　　1000＞0999

　　0.30＞0.23

　　即用“0”占齐无效数位，在“等位数长度”的情况下，只用方法②从高位到低位一位一位地往下进行同位相比。

　　或许，小数的性质就是要婉转地告诉我们：数位数并不是比较数的大小的本质方法，它只是一种同样凑巧（指碰到了整数）的简便方法；从高位一位一位地往下进行同位相比才是最重要的。

　　（重要程度★★★★）

　　（3）分数的基本性质既揭示了分数的特点，又为通分、约分提供依据。

　　如同小数一样，分数也拥有无穷多的等价变形：

　　就像0.5是最简形式一样，分数也有一个最简形式，就是分子、分母是互质数的时候，也就是公因数只有1的时候，这时的分数叫做“最简分数”，比如上面的二分之一。一个分数由“最简形式”到“不简形式”，或由“不简形式”到“最简形式”，是可以自由切换的，它们遵循的规则就是：分数的基本性质。

　　约分的过程，其实就是不断地对分子、分母除以它们的公因数，使其分子、分母不断变小，直到“最简分数”：

　　通分的过程恰好相反，就是不断地扩大分子、分母，在无穷无尽的分母中，总会傻傻地找到相同的分母的（此时分数的计数单位相同，可以直接进行加减法计算）。当然大家知道，有了“最小公倍数”之后，我们完全不用这么傻，此处只是尽力还原问题最开始的情况：

　　（4）比的基本性质可以用来化简比，寻找比例。比如：

　　10：25＝（10÷5）：（25÷5）＝2：5

　　6：10和9：15

　　6：10＝6÷10＝0.6

　　9：15＝9÷15＝0.6

　　所以：6：10＝9：15（表示两个比相等的式子叫做比例）

　　比可以写成分数形式，比如：

　　自上而下读为：10比25；而不是自下而上读为：25分之10。这种形式似乎说明“比的基本性质”和“分数的基本性质”完全等价。我找不出十分突出的差别，因为它们在本质上确实一致。我只找出了一些细枝末节的东西，比如“最简整数比”不再像“最简分数”那样成为比的表现形式的唯一追求。有时，人们对比的前项是1或后项是1的比更为青睐，比如：

　　10：25＝1：2.5＝0.4：1

　　1所代表的数量，往往是作为参考的“基准”的。仔细阅读您的数学书，或者仔细留意生活，您会发现这一点的。比如：地图中的比例尺就会使用这种习惯。

　　本次的复习就至此打住吧。

　　再会。

,