金字塔和天文学的关系（金字塔日晷与三角学）

在数学领域中，可能没有其他分支学科能像三角学一样始终占据着中心位置。—— 赫伯特

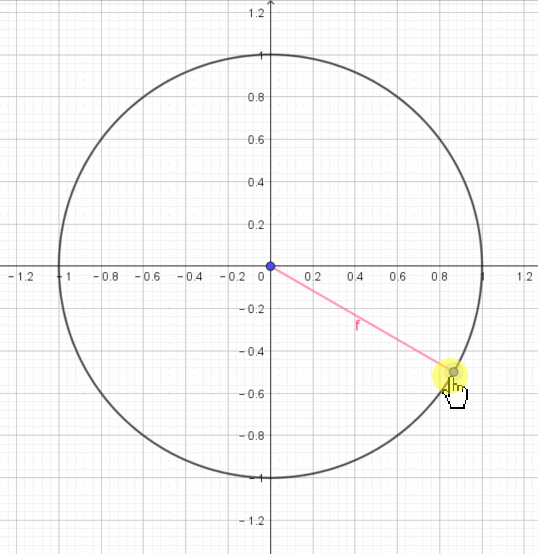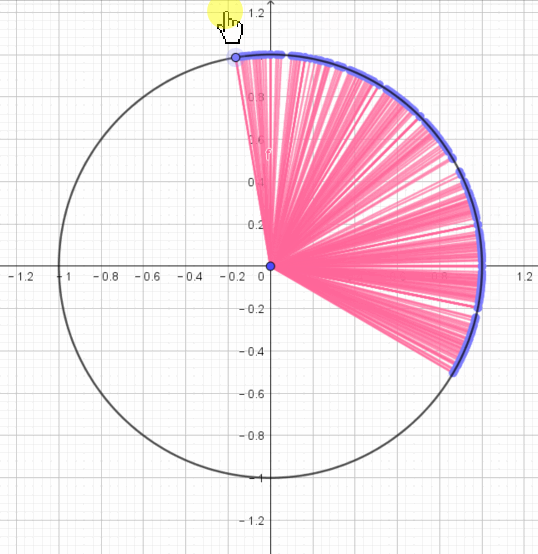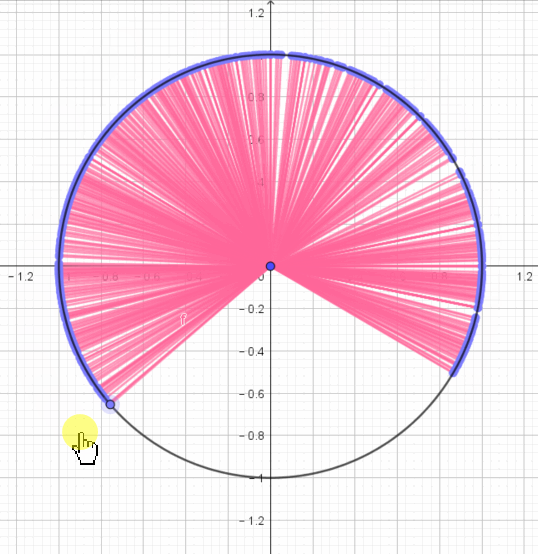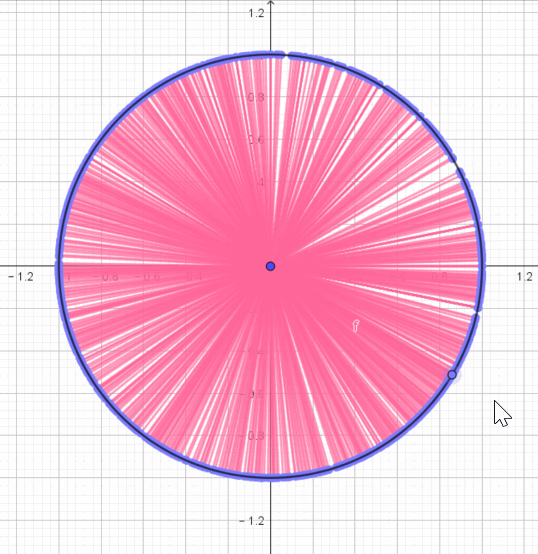
角和圆

➣ 角代表了什么？

在纸上随便画出个角，很容易就发现角是由两条射线确定的，或者说是由一条射线转动形成的。转动的幅度就是角度。

➣你有没有想起一个几何图形？

圆是怎么定义的呢？线段转 1 圈，轨迹就是圆。

角和圆关系很大，都是转动形成的，只不过形成圆的线长度是固定的；形成角，只要是线就可以。

➣ 圆和角有什么关系呢？

圆是角的特殊情况，但增加了三个限制条件：

1. 转动主体是线段，而不是射线。也就是说转动的主体长度是有限的，是收敛的。
2. 在转动的过程中，线段的长度是不变的。
3. 转动幅度有限制，当转回原点时停止，也就是转了一圈。

➣ 第 1 个限制产生了什么作用？

这会让转动的过程形成曲线轨迹。

这个限制产生了一种“收敛”的作用，角和圆弧的关系，就好像射线和线段的关系一样，“弧”是在角上增加均匀的距离限制产生的。

所以，很容易就会想到“弧”和“角”是对应的，“弧”只不过是把“角”这个发散的形状收敛了。

➣ 第 2 个限制产生了什么作用？

这会让转动的过程形成优美简洁的“圆弧”曲线。圆给人一种简洁优美的感觉，因为它是均匀的，上面的每一个点到中心的距离都是一致的。如果没有这个限制，那么运动轨迹可能是一团乱麻。

➣ 第 3 个限制产生了什么作用？

刚好转了一圈，如果从静止角度来看，平面上最大的角就是圆所对应的角，任何其他的角都可以表示在圆中。

自然而然的就要把“周角” 平均分割 来作为“角度”的单位；又因为圆是均匀变化的简洁优美的图案，所以研究角的时候经常要放到圆形中去研究。

所以说，“圆”是一个研究“角”的平台，早期的三角学是建立在“单位圆”基础上的。习惯上把“圆”这种特殊的角叫做“周角”。

➣怎么样度量角的？

最常见的单位就是“度”，在右上角有一个小圆圈 °。把一个周角等分 360 等份，其中的每一份就叫做 1 。

其实仔细想一下就觉得很奇怪，因为其他公制单位都不是 360 进制的，唯独角度是 360 进制。这到底是怎么回事呢？具体的缘由已不可考，但可以知道的是这种表示方法是古巴比伦人最先使用的，他们的计量进制正好是 60 进制，也许与此有关吧。[3]

➣ 弧度是怎么出现的？有什么好处呢？

在数学和物理中，我们最常用的其实是弧度而不是角度；国际单位制中就是用的弧度(rad)。

之所以用弧度，是因为“弧线”它是个两面派，从度量角度来说，它是“线”，可以用公制度量“长度”来描述，但是从性质上来说属于转动，因为弧是角限制距离形成的，几乎就是一回事。

所以就直接用单位圆(r=1)的弧长来描述角度，这和国际单位兼容得很好，在弧度制下，公式变得非常简洁，所以弧度制这才是数学和科学中最主流的。

比如，用弧度描述半径为 r 的圆的周长 s 就是：s=rθ，因为弧度 θ 就是单位圆的弧长，我们要描述的是半径为 r 的圆，自然就是 r ×θ ；如果用角度来描述就麻烦多了，s= πrθ/180 。

➣ 为什么会这么麻烦呢？

单位圆的周长是 2π，所以 2π=360°，1 弧度就是 180°/π，故

弧就是圆的一部分，所以在描述最基础的图形之一——圆的时候，就非常简洁；而用角度就占不到任何优势了。

弦

不过就算是弧度制，想知道角的具体度数也是非常难的。如果角度很小，就画在一张纸上，那可以简单的用尺子量一下。

但如果要建造一个建筑物，怎么样才能保证墙壁的倾斜角度是一致的呢？

尺度稍微放大一点，之前测量角度的方法就不灵了，所以我们急需一个更简单的角度测量和比较。

➣ 那为什么不直接测量弧长呢？

因为弧是一个曲线，曲线的长度并不好测量。既然是这样，我们很自然的就会想到，弯的不好了，那我们可以量直的呀。

这个想法如此自然，以至于世界各地的古文明几乎都会想到弦这个概念。我们中国人用弓弦来命名这条弦；西方人则用琴弦(Chord)。[4]

➣怎么通过弦长得知角度？

角度的变化和弧线的长度变化是对应的，它们都是旋转的结果，是成比例的，所以他们之间的关系也就是正比例函数(一次函数)：

。如果半径确定，那么角度和弦长就一一对应。

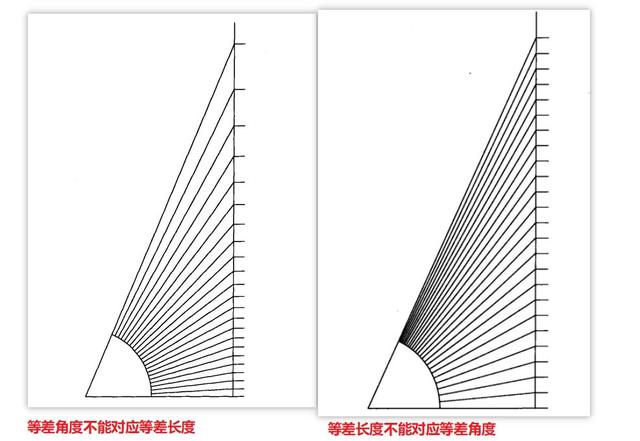
但是线和它们并不是一伙的，线属于延长，角属于旋转，所以长度的增加和角度的增加并没有一个简单的比例。

定量的描述并不容易，不过定性就简单多了。

在半径确定的情况下，如果两个弦长是一样的，角也是一样的；或者说通过半径和弦长(两个线段)的比值[2]，就可以定性的判断角是否相等。

▌金字塔中的原始三角学

仔细看看金字塔的图，你会发现它居然是一个非常完美的正四棱锥，对于 4000 年前的人来说，在施工中保持墙壁倾角的统一，似乎是一件不怎么容易的事情，他们到底是如何做到的呢？

有 4000 年历史的金字塔身上有很多谜团，不过幸运的是这个问题，我们已经知道了答案。

➣金字塔的秘密是如何被揭开的呢？

因为发现了一本古埃及的数学教科书，而最后一个问题又和数学紧密相关，这本书就是《莱因德数学纸草书 》，是已知年代最久远，内容最广泛的数学文献，第56题到第60题都是关于金字塔的内容。[1]

金字塔高 250 腕尺，底边长 360 腕尺，它的“塞克特”是多少？

➣“塞克特”是什么意思？

从后面的解答来看，“塞克特”是金字塔 高度 h 与 边长的一半 a/2，的比值。知道了这两条线段的长度，也就确定了倾角 θ 。

➣那么具体是如何操作的呢？

之所以不通过测量斜边，而是通过测量高度和底边长度来比较倾角，是因为在施工中后面的两个量是容易得到的。

仔细看金字塔的图篇，会发现其表面并不是光滑的，而是台阶状的。每当施工出一个台阶之后，就会知道这个台阶的高度 Δh ，从上面垂下绳子，就能测量 Δh 对应的底边长度 Δa ，从而计算出“塞克特”，保证这个值和预期的一致，也就保证了施工的质量。

建造金字塔时保证倾角相等，就是通过两条线段来测量推算角度的过程。

古埃及人用三角学建造金字塔，中国人则用它计时。

日晷所要测量的是太阳与地平线的夹角，已知日晷“规”的长度，再测其影子的长度，太阳的夹角知道了，背后对应的时间也就知道了。

原始的三角学不仅让金字塔得以施工，还能够让后世的法老知道金字塔到底有多高。

测量金字塔高度的过程，就是通过角度和一条线段的长度，来推算另一条线段长度的过程。

总结

1. 角的度量：角的常用单位有两个，角度是等分周角360份产生的；弧度是圆弧的长度。弧度在科学中更常用，因为会让公式更简洁。
2. 圆弧和角的关系：圆弧是角均匀收敛产生的轨迹。
3. 原始三角学：祖先们意识到了角度和长度之间是有关系的，并且利用这种关系来计时和建造金字塔，但是他们的认识仅限于定性。

注释

[1] 其实最初的时候，人们并不知道上面的文字代表什么，因为埃及的象形文字早就已经失传了，没有人能够读懂。用文字破译之后，大量的埃及文献才得以被翻译。象形文字的破译又是一段传奇的故事，是托马斯 · 杨、商博良和罗塞塔石碑之间的故事。

[2] 任何两条线段都可以看成是圆的半径 r 和弦 s ，半径确定圆的大小后，弦决定就决定旋转角度。值得注意的是，我们的讨论几乎都是在“单位圆”(比例)中进行的，为的就是排除“半径不确定”(等比放大)这个干扰因素，直接讨论这个关系的本质。这种思考方法非常像科学研究中的“控制变量”。

[3] 时间单位也是 60 进制，估计是因为钟表就是圆形的。

[4] “正弦”并不是这里的“弦”，后面会谈到。

▌相关文章

» 文章 | 角的疑惑——为什么使用弧度？

» 文章 | 科学和哲学之祖: 泰勒斯

,