高中数学单调性导数综合压轴大题（高中数学导数压轴题的一类问题）

尤其当我们面对压轴题——导数大题时，一些同学导数题求完导就不写了，甚至有的同学直接空着，实在是对分数的浪费，浪费就是犯罪啊！小编今天分享给大家的是解决这种导数题里的一大类问题方法——含参函数单调性分析。

一、 不含参时单调性分析

一旦函数含有参数，很多同学会认为很复杂，不会进行分类讨论，其实最主要的还是有的同学们对分析函数单调性的整个过程还不够熟练，我们先通过分析不含参的函数单调性来看一下总共需要进行哪几个步骤。

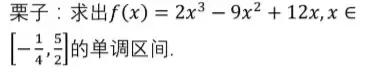
2、 求导通分：（不要问我为什么要求导，手动微笑脸）单调性极值最值问题一定是要求导的，求导就是干这个的，所以我们求出导函数。

令导函数大于等于零，解出来的范围就是单调递增的范围。

3、 解不等式：一般来说你会得到一个一次或者二次不等式，二次居多。解这个二次不等式，不熟练的同学可以画出大致这个二次函数图像。

一般来说二次函数和x轴可能有0～2个交点，这里是2个根，我们用x1，x2表示，所以符合条件x的取值范围是两根的两边。我们可以通过因式分解或者求根公式的方式求出这两个根。

这里两根的结果为1，2所以

4、 考虑定义域写单调区间：

最后结合给出的定义域，我们需要分析二次函数两个根与定义域之间的位置关系，最后我们写出

这样一个不含参的函数单调性分析并不困难，但如果你觉得含参问题很复杂的话，一定要先熟练不含参的分析过程，里面很多地方是后面分类的原因。

可以说只要你不含参分析做的够熟练，含参的分析就完全难不住你！

二、 含参函数单调性讨论

1、 看定义域：还是老样子，不管什么时候，首先写出定义域。

2、 求导通分：这里的求导有些复杂，基本功一定要扎实，不熟练的话可以一步一步去求导。一般来说求导的结果都会包含着一个含参的一次或者二次函数。

求完导为什么感觉没有二次函数呢？！

利用求导乘法公式和除法公式，最终得到导函数，并且通分才能看到这个二次函数。最终化简得这个导函数。

现在终于能看清楚了！所以我们

这个时候的解集就是单调递增区间。这个不等式看上去很恐怖，但是一般来说除了含参二次函数，其他部分的正负情况都是可以直接确定的。

平方一定是正数，指数函数也是恒正的。

3、 解不等式：

这个不等式解出来的的范围其实就是单调递增区间。

接下来大家要想一下，解二次不等式的时候，我们要需要把这个二次函数和轴的两个交点找到，然后在结合二次函数图像去判断的取值范围。接下来我们看一下怎么去解一个含参二次不等式。

（1）讨论二次项系数

这个函数图像大致长什么样子呢？他一定是二次函数么？就算是二次函数开口方向又是怎么样的？，所以我们在求解含参二次函数的时候首先对二次项系数进行讨论，大于零小于零等于零？这决定了他的开口方向。

这题题设告诉我们a＞0开口向上已经确定，我们就不需要进一步讨论了，那么我们看下一步。

（2）讨论判别式

为了求出解集，我们得知道二次函数等于零时候的根x1，x2，但是这个根一定存在么？根存不存在会直接影响到解集，所以我们必须分开去讨论。

1，

此时结合开口方向，图像整体在轴上方

不管x取多少，二次函数都在x轴上方，所以这种情况下

的解集是一切实数，那我所说的这种情况是那种情况还记得么？

这就是

的时候，我们看下此时a对应的取值范围

这个时候是的情况，但是别忘了本身是有范围的，

这个时候我们可以结合图像写出不等式的解集

最后考虑一下定义域，给出第一个分类下的结论

2，

结合开口方向，图像与轴有两个交点

从图像可以看的出我们只要找到两个根就可以了，二次函数大于零的范围就是两根的两边。

这种情况我们就要先求根了，在求根的时候，如果可以因式分解，可以优先因式分解，如果不行的话，那就老老实实用求根公式。

最后我们要考虑定义域了，但是这个X≠1要挖掉的1应该写在哪里呢？应该放在的X1X2两边呢还是中间呢？我也不知道。我们先看下他们的大小关系是不是确定的，是，最好，不是的话我们就分情况写出不同的结果。

说明两个根和1的关系如下图，所以最终的单增区间如下

4、 结合定义域写单调区间：我们在每种讨论最后写单调区间之前都要比对一下，解集和定义域的关系，单调区间一定要放在定义域当中才可以，如果两根和定义域大小关系可以确定的话我们可以直接写单调区间，如果不确定的话，你还要进一步分类，对应的不同情况下，单调区间的写法会不同。

这些导数大题本身综合性都很强，所以想解决压轴题的同学一定要先熟练使用所有的求导公式，多画图帮助自己分析含参的二次函数。

来源 | 网络

,