高中数学解立体几何题求异面角（高一数学立体几何二面角问题求解示例）

有高一学生对立体几何中二面角平面角的找法和求法不是太熟悉，今天选两个典型案例予以说明，高一阶段二面角平面角的作法在上次推送中给出了说明，此次内容只对应第二种投影法，以二面角P-AB-Q为例，投影法即从平面上一点P出发向平面ABQ作投影H，再从H点向交线AB作垂线，垂足设为K，则∠AKH即为所求二面角的平面角。

投影法的难点在于确定出投影点H的位置，有时候点P在平面上的投影点并不在三角形ABQ中，所以常用的处理方法为将三角形ABQ所在平面扩展，至于如何扩展平面可使用平行线法或交线法，视题目而定。

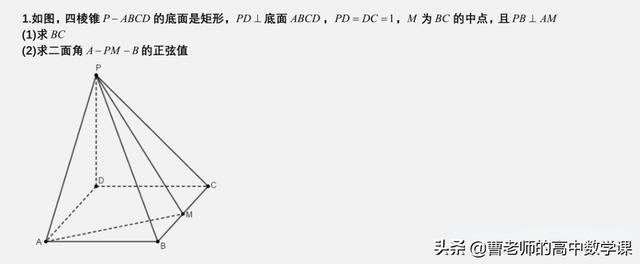
PD垂直底面，且底面为矩形，若补全为长方体，BC//PA1，可将平面PBM补全为平面PCBA1，而过A点向平面PCBA1点作投影，投影点恰好为A1B的中点，投影点找到了，二面角的平面角也就找到了。

找到平面角之后，AK不能直接求出，可通过求HK间接求出AK，当然也可以直接求正切值，求HK时将HK放到所在平面中利用等面积法即可，这也是此类问题常规的套路。

这是2022年新高考一卷中的题目，高考中所有的立体几何都可以用纯几何法去解，若熟悉之后几何法并不比向量法复杂，反而更简单直接。

根据已知的面面垂直且A1B为交线，AA1=AB，所以取A1B的中点E,连接AE即可知AE垂直平面A1BC，且A1BC和平面BDC共面，所以A点在平面BDC上的投影就确定出来，再从投影向交线作垂线即可，之后依旧利用等面积法求出其中一条直角边即可。

高一立体几何求二面角的题目不会很难，把前两种解题方法理解透掌握住就可以了，高一遇到的几何体相对规整，无论是线面角还是二面角都较容易处理一些。