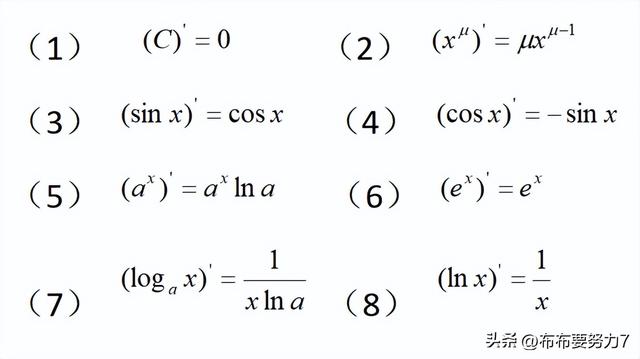高中数学导数基础知识讲解（高中数学导数学习）

同学们我们又见面啦！今天我们来学习导数：

不含参函数单调性

例1. 已知函数

讨论函数的单调性

解：由题意可知当然是先求导，得

然后通分，可得

在这里注意一下，可能是由于个人习惯我一直喜欢把最高项放在最前面。好了，接下来就是要对其进行化简，能因式分解的一定要因式分解

值得注意的是这里面的x的取值范围是大于0的，因为lnx中真数是x的缘故啊！

所以接下来我们只要讨论-(x-2)的正负了

好的，我么首先令

众所周知，普遍状况下如若

因此可以解出，过程如下：

即当x∈(0,2)时，f(x)在此区间单调递增，同理可以得出当x∈(2, ∞)时，f(x)在此区间单调递减

然后就是综上所述，呈上最终的你的结论……

好的现在我们一起来做一下总结，针对上面的一系列过程

过程总结

1、第一步就是进行求导，这里面需要注意的是指数函数求导与对数函数求导，那么主要的哪两个呢？

2、求导完了之后就是要把零散的式子联系在一起就要通分，然后进行因式分解(大多数是要因式分解，而且还大多数是可以的)

3、在能够进行因式分解的前提下我们或许已知某些未知数的范围了，并根据这些范围确定部分式子的正负性，比如上面的解题过程当中的x或者x 2的正负性。

4、在得知部分正负性之后就要求出f(x)′的零点，或者你可以直接令f(x)′＞0或者f(x)′＜0来求出其单调区间（注意哦，如果这里求导出来的是恒正或者恒负那么我们就可以直接判定其单调性，如果不是那也只能分区间进行讨论的）

5、讨论完毕之后那么还请你写出最终的结论吧，要不然会扣分的

在这里我得强调一下，在真正的解题过程当中是完全没有必要这么复杂的，完全可以几步就把这个搞定，这里只是尽可能的把每一个环节讲清楚，有点啰嗦，但同时也是为下一讲“含参函数单调性”做铺垫！

以下附上我写这篇文章的word草稿，大家可以看一下

天，小编为大家总结了导数9大答题技巧，帮助大家再高考数学答题中搞定导数，多拿一题的分值，轻松拿下140

“导数”

拿到手不是你的，吃透，嚼烂，吸收才真正是你的，分享给更多想要提升数学成绩的高中生吧

更多教育资讯关注索科教育

(本文图片文章摘抄于网络如有侵权请联系我们删除SY519-)

,