群论与抽象代数（因为解方程而打开的抽象代数大门）

西方的几何公理体系，与东方的代数算法体系，是古代数学的2个不同脉络。

几何，早在古希腊时代就已经建立了公理化的体系。

代数，实际上直到近代才真正地公理化。

在群论被创立之前，代数实际上只是一些解方程的算法，更类似工程而不是科学。

一元一次方程：2x = 2，

解：x = 1。

两边除以2就行，为什么？

别说回答这么复杂的问题，就是回答什么是乘法、除法、加法、减法，在抽象代数诞生之前，都难以公理化的描述[捂脸]

所以说，古代解方程的方法是应用数学算法，而不是数学理论。

代数的公理化，远比几何的公理化更难！

代数脱胎于算术，很早就被人们所熟知，反而更容易让人忽视，更难对它进行深入的研究。

熟视无睹，直到解5次方程时遇到了困难：给不出求根公式[呲牙]

也就是从这时候，人们才开始研究加减乘除到底是什么？

这已经到了17世纪，伽利略观察木星的时代了。

1，方程的诞生，

鸡兔同笼问题，是小学数学的基本难题，可能没有之一。

如果不用方程，用算术怎么解？

“鸡兔同笼，有20个头，60只脚，问鸡、兔各有多少个？”

解：

假设20只全是鸡，那么有20x2=40只脚。

脚数跟总数的差额是60-40=20只。

如果把1只鸡换成1只兔子，可以增加4-2=2只脚：那么，要换多少只兔子，才可以补齐20只脚的差额？

20 / 2 = 10只兔子。

20 - 10 = 10只鸡。

头数：10 10 = 20。

脚数：10x2 10x4 = 60。

求兔子只数的总算术式：(60 - 20x2) / (4 - 2) = 10，

进一步获得鸡的只数：20-10=10。

如果使用方程的话，我们使用二元一次方程组，设x只鸡，y只兔子：

x y = 20, (1)

2x 4y = 60, (2)

(1)式乘以2，可得：2x 2y = 20x2 = 40，

(2)式减去(1)式，可得：4y - 2y = (4 - 2)y = 2y = 60 - 40 = 20，

进一步可得：y = 10，

最后可得：x = 20 - y = 10。

解方程的步骤，与算术的步骤是一样的，只是算术更抽象，都是间接运算，而方程是直接运算。

算术，相当于是在刚研究问题的时候，就要展开问题的解法。

所以，算术对人们的思维深度要求更高，对大脑的信息迭代速度要求更高。

如果是一般人不会拿算术求解，很多人会说你笨，但当问题复杂到大牛也没法拿算术求解的时候，大牛就发明了方程[捂脸]

实际上，大牛的大脑也迭代不动了，然后他就换了思路：既然逆向思考太难了，干嘛不设个未知数，正着来呢？

于是，以后的所有问题，都变成了解方程的问题。

就算是欧几里德辛苦创立的几何公理体系，也被笛卡尔嫌弃“只能锻炼人们的思维”，然后笛卡尔发明了解析几何[呲牙]给他变成了代数方程。

笛卡尔：“我希望之后人们可以真正地解决问题，而不只是锻炼思维。”

“两点可以确定一条直线吗？”

ax by = c确定一条直线：又精确，又直接。

2，解方程是个问题，

ax b = 0，解：x = - b / a.

......

代数方程的求解问题，是个因式分解问题。

只要多项式能够分解成一次式的乘积，那么就可以获得n个根（n为次数，包含重根），即：

多项式的分解，当然是依赖于系数的：因为不同的多项式变化的是系数，而次数是固定的，缺项可以看作系数为0。

根与系数的关系，早在16世纪的意大利和法国就被注意到了，即韦达定理：

韦达定理还可以从2次方程继续扩展到高次方程：根的和与n-1次项的系数有关，根的积与常数项有关（具体的可以查看代数书）。

虽然人们在16世纪就发现了根和系数的关系，但是，5次方程的求根公式就是给不出来。

因为，人们甚至没法说清楚：加、减、乘、除、开方，到底是什么？

求根公式，根式解，人们从古代一直用到18世纪，依然说不清这些运算的本质。

3，加、减、乘、除、开方，到底是什么？

减法是加法的逆运算，除法是乘法的逆运算，这是人们熟知的。

开方是什么？

（如果x^n = y，那么x就是y的n次方根，这个定义没什么用）

我们先从2次方程的求根公式开始：

为了简单，可以让a = 1，即方程的左边是首一多项式。

为了让方程的判别式不成立，从而产生虚数，可以看这个方程：

它在复数里是有解的：-1 i, -1 - i。

但在实数里是无解的，在有理数里当然也无解。

-1 和 i 是没法合并同类项的，因为它们2个处于不同的维度：

画在图上时，-1在x轴，i在y轴。

x^2 2x 2的两个根

可以看出，解这个系数全是实数（有理数、整数）的方程时，居然需要跑到复数里才可以！

所以，高次方程本质上是扩大了数的范围：它的根与系数可以在不同的数集里。

仅仅是2次方程，就可以把根映射到复数里。

f(x) = x^2 bx c = (x - x1)(x - x2) = 0，它确定的是(b, c)与(x1, x2)之间的函数关系，这个关系是一一对应的，因为它们都表示同一个方程。

A：知道系数求根，有2次方程的求根公式。

B：知道根求系数，直接把根代进去，就是系数的一次方程。

当x1 != x2时，范德蒙德矩阵的行列式不为0，所以上面的线性方程组有唯一解：

即，多项式方程（在没有重根时）是根与系数的一一对应关系。

这个对应关系，可以把实数的系数映射到复数的根，或者反过来。

所以，对于一般的高次方程来说，求根的前提是扩大数的范围。

更准确地说，是扩大数的维数。

因为整数对除法运算的结果不闭合，所以研究方程的解时，最小范围必须是有理数Q。

如果在整数范围内，那么一元一次方程都可能无解，例如2x = 1。

要为了求根而扩大维数时，扩大的基础就是有理数Q。

4，那么，加法和乘法是什么？

通常的加法，是有理数Q上的一个二元运算符，它表达了一个对应关系：z = a(x, y)。

通常的乘法，也是有理数Q上的二元运算符，它也表达了一个对应关系：z = m(x, y)。

找出它们两个的共同点来，就是群论：

一个集合，与定义在它上的二元运算符，符合哪些公理[捂脸]

公理1，结合率：a (b c) = (a b) c, a x (b x c) = (a x b) x c.

公理2，单位元和逆元：a (-a) = 0, a x (1/a) = 1.

加法的单位元叫0，俗称零元。

乘法的单位元叫1，俗称单位元。

在代数学上，这就是0和1的本质，符合这个条件的都可以叫0和1。

公理3，交换律：a b = b a, ab = ba.

加法是肯定符合交换律的，因为加法的两个元素是同类。

乘法不一定符合交换律，因为乘法的两个元素不一定是同类。

之前的文章里举过例子，1个盘子里有5个苹果，3个这样的盘子，总数有多少个苹果？

解：5x3 = 15，5是苹果的个数，3是盘子的个数，3和5在这里并不是同样的含义。

所以，矩阵乘法的“不交换”是正常的，整数乘法的“交换”才是特例。

所以，加法和乘法的区别，就在于符不符合交换律！

所以，减法和除法并不存在，存在的只是加法和乘法的逆元。

所以，一元一次方程的求解问题，就是求加法和乘法的逆元问题。

求逆元需要几步运算？1步，见公理2。

所以，一元一次方程的求解只需要2步：第1步求加法逆元，第2步求乘法逆元。

方程：ax b = 0，

求加法逆元：ax = -b，

求乘法逆元：x = -b/a，完成。

当未知数前面的系数是乘法的单位元时，就是一元一次方程的解。

多个未知数的一元方程组的解，都通过加法和乘法运算，先转化成一元一次方程。

5，那么，开方是什么？

在第3节里说了，高次方程本质上是扩大了数的维数，扩大的基础是有理数Q。

那么，从有理数到实数需要扩张多少个维数？

无穷个，因为

所以，不能直接在实数域里考虑高次方程的求根问题，而是一点点的扩张。

例如：

方程1：x^2 - 2 = 0，它的求根实际上只需要扩张一个数，

方程2：x^2 - 3 = 0的求根，只需要扩张一个数，

方程3：x^2 - 6 = 0的求根，在上面2个扩张的基础上，它不需要再扩张了，因为6 = 2x3。

6是合数，当它的所有质因数的平方根都被扩张进去之后，它的方程x^2 - 6 = 0已经可解了。

方程4：x^2 - 8 = 0的求根，也只需要扩张就行，它的解是

所以，就可以满足上面4个方程的求根，不需要扩张到整个实数R。

开方运算，本质上是有理数域的扩张，域的扩张。

6，域是什么？

域，是能够进行加法和乘法运算、和它们的求逆运算的最小封闭集合。

如果只定义1种运算（加法或乘法），并满足结合率、单位元、逆元的集合，叫群。

如果定义了2种运算（加法和乘法），并满足分配律的集合，叫环。

公理4，分配律：a x (b c) = ab ac，(a b) x c = ac bc.

在环的基础上，还可以求乘法的逆元，就叫域。

加法的逆元是肯定存在的，整数就可以满足封闭条件。

乘法逆元的存在，可以得出这个公理：

公理5，消去律：ab = 0，所以a = 0或b = 0.

如果a != 0，它就存在乘法逆元，即倒数1/a，左乘1/a就可得b = 0。

如果b != 0，它就存在乘法逆元，即倒数1/b，右乘1/b就可得a = 0。

域的0之外的元素，都有逆元。

所以，有理数Q是个域，实数R是个域，复数C是个域。

但是整数Z不是域，它只是个环。

所以，方程的根式解问题，是有理数域Q的一个有限根式扩张问题。

根式扩张之后的域，叫做多项式的分裂域（用F表示）。

F是Q上的一个有限维线性空间。

，是什么？

是系数为(4, 8, 16)，基为的一个线性表示。

F除了Q之外的其他元素之间的对应关系，是关系到高次方程是否有根式解的关键。

这个对应关系，叫做伽罗瓦群Gal(F/Q)。

7，伽罗瓦来了，

伽罗瓦定理：一般5次方程的根式可解，当且仅当它的分裂域对应的伽罗瓦群是可解群。

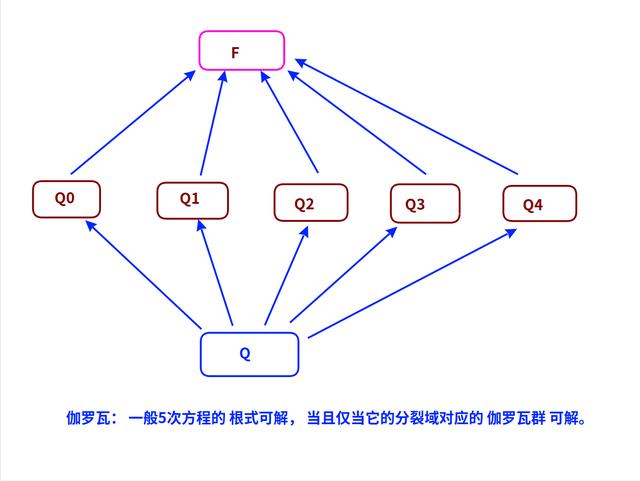
伽罗瓦理论

可解群是什么？

就是群中的元素，可以沿着一条链变换到群的单位元。

ax = b要是求解，只需要把系数a变成1，乘以1/a就行，所以一元一次方程是可解的。

群的元素不一定是数字，也可以是对应关系（置换）。

所以，有时候换过来之后，换不回去。

魔方的旋转，就是一个群

8，为什么有的方程没有根式解？

因为加法和乘法运算会消除信息。

f(x) = (x - x1)(x - x2)(x - x3)(x - x4)(x - x5) = 0，这个方程是完全信息的。

它的根就是x1, x2, x3, x4, x5。

但是，把它展开之后就不是这样了：

f(x) = x^5 (x1 x2 x3 x4 x5)x^4 ...... (-1)^5 x1x2x3x4x5

= x^5 ax^4 bx^3 cx^2 dx f = 0.

加法运算，是肯定会消除信息的。

4 = 1 3 = 2 2，光看到4是不知道它由哪2个数字加出来的。

乘法运算，在2个乘数不全是质数的情况下，也会消除信息。

54 = 6x9 = 2x27 = 3x18，也是没法确定它是哪2个数字乘出来的。

所以，有些方程没法从系数反回去求根，就是必然的。

9，法国大数学家、群论的创始人、伽罗瓦，

又是法国[捂脸]

伽罗瓦出生于1811年，1832年过世，年仅21岁。

他从16岁学数学，5年之后创立群论，论文曾经寄给柯西、傅立叶。

柯西把这篇数学史上最著名的论文给搞丢了，而傅立叶收到论文后恰好病逝。

然后，伽罗瓦因为一个女人（斯特凡妮）而卷入了一场决斗，死时只有21岁。

伽罗瓦在决斗前一天的晚上，写下了他的数学理论，让人送给了高斯、刘维尔。

刘维尔花了十几年的时间，把伽罗瓦的理论整理出来，用更通俗的语言再次发表，群论才流传下来。

伽罗瓦，1811-1832

,