电学并联电路（电学课程1直流-第5章）

什么是“串联”和“并联”电路？

仅由一个电池和一个负载电阻组成的电路分析起来非常简单，但在实际应用中并不常见。通常，我们发现电路中有两个以上的元件连接在一起。

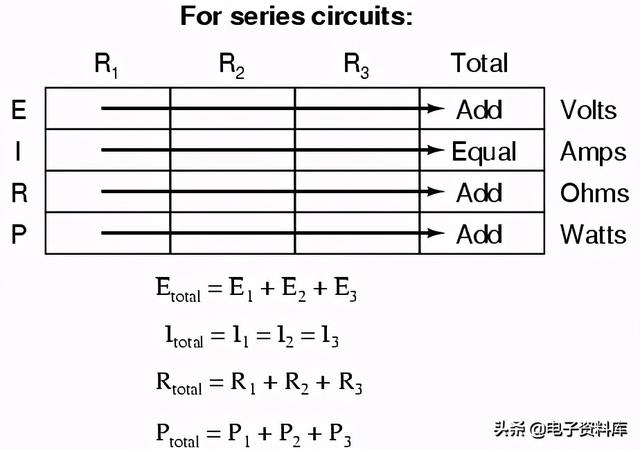
连接两个以上电路元件的基本方法有两种：系列和平行. 首先，一个串联电路的例子：

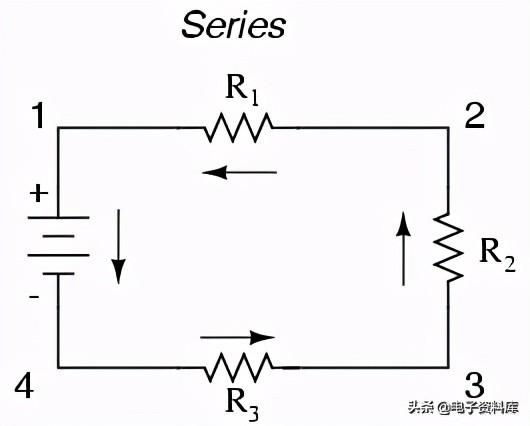
这里，我们有三个电阻（标记为R1，R2，和R3)，从电池的一端连接到另一端。（需要注意的是，下标标签——字母“R”右下角的那些小数字——与电阻值（欧姆）无关。串联电路的定义特性是电子只有一条流动的路径。在这个电路中，电子以逆时针方向流动，从点4到点3，再到点2到点1，再回到4。

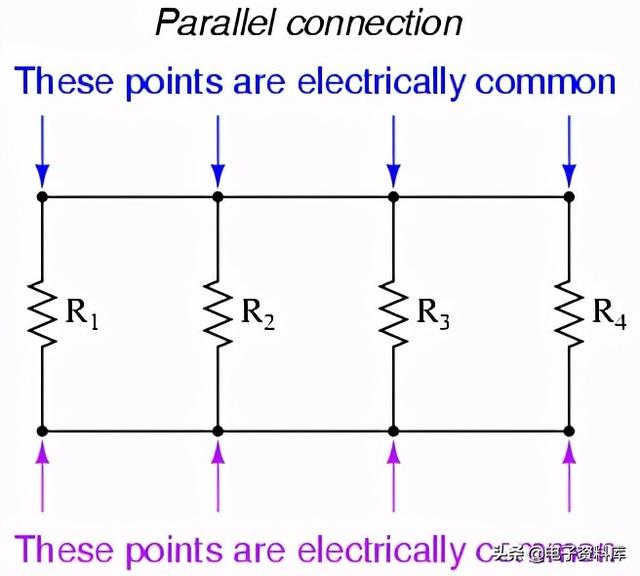
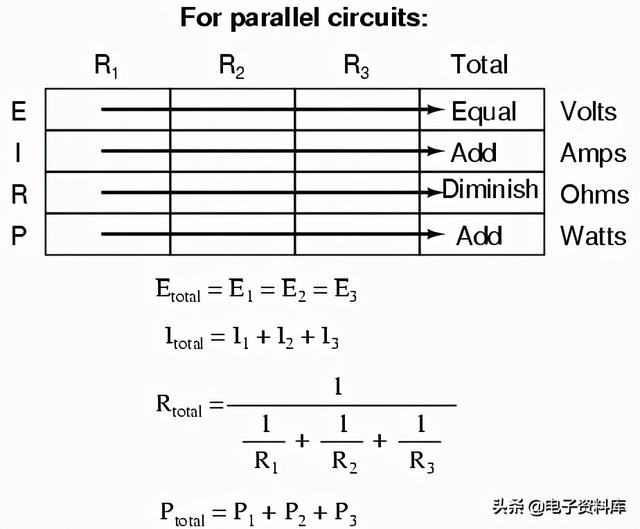
现在，让我们看看另一种类型的电路，并联配置：

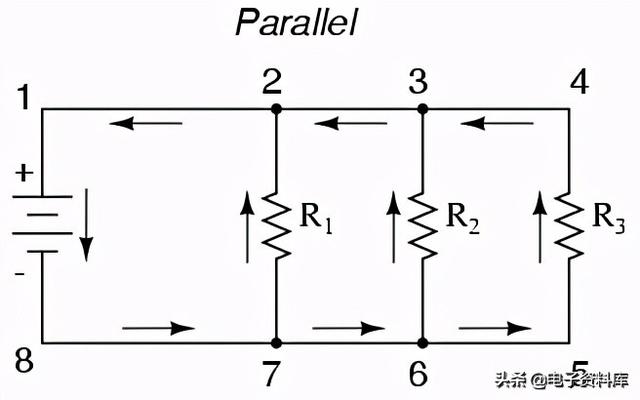
同样，我们有三个电阻，但这次它们形成了不止一个连续的电子流动路径。有一条从8到7再到2再到1再回到8的路径。还有一个从8到7到6再到3到2再到1再回到8。然后有第三条路径从8到7到6到5再到4到3到2再到1再回到8。每个单独的路径（通过R1，R2，和R3)被称为分支 .

并联电路的定义特性是所有元件都连接在同一组电气公共点之间。看一下示意图，我们可以看到点1、2、3和4在电气上都是公共的。第8、7、6和5点也是如此。请注意，所有电阻器和蓄电池都连接在这两组点之间。

当然，复杂性也不局限于简单的串联和并联！我们也可以有串联和并联的电路：

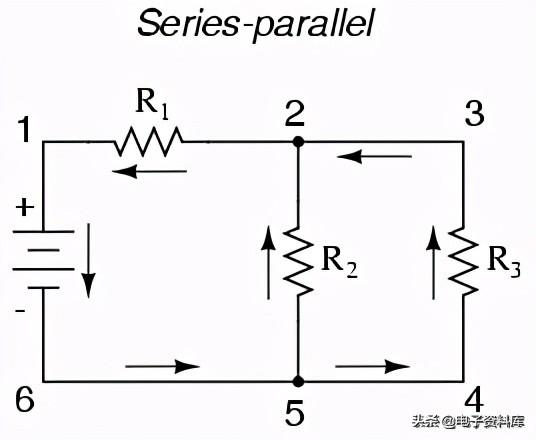
在这个电路中，我们有两个回路让电子流过：一个是从6到5再到2到1再回到6，另一个是从6到5到4再到3到2到1再回到6。注意两条当前路径是如何通过R1的（从第2点到第1点）。在这个配置中，我们可以说R2和R3相互平行，而R1与R2的并联组合和R3串联.

这只是对未来事情的预告。别担心！我们将详细探讨所有这些电路配置，一次一个！

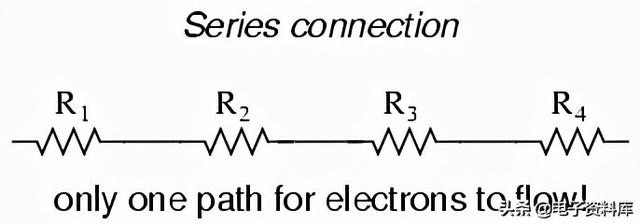
“串联”连接的基本思想是将元件端到端连接在一条线上，形成一条供电子流动的单一路径：

另一方面，“并行”连接的基本思想是所有组件都通过彼此的引线连接起来。在一个纯并联电路中，无论连接了多少个元件，都不会有超过两组电气公共点。电子流动的路径有很多种，但所有元件只有一种电压：

串联和并联电阻配置具有非常不同的电气特性。我们将在后面的部分中探讨每个配置的属性。

• 回顾：
• 在串联电路中，所有元件都是端到端连接的，形成一条供电子流动的单一路径。
• 在并联电路中，所有元件相互连接，形成两组电气公共点。
• 并联电路中的“支路”是由一个负载元件（如电阻器）形成的电流通路。

简单串联电路

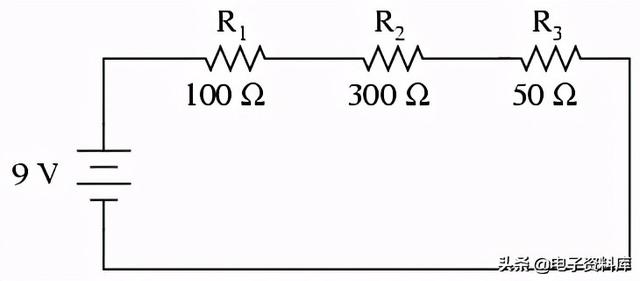
让我们从由三个电阻和一个电池组成的串联电路开始：

了解串联电路的第一个原则是通过电路中任何元件的电流量都是相同的。这是因为电子在串联电路中只有一条流动路径，而且由于自由电子像管中的弹珠一样流过导体，所以电路（管）中任何一点在任何特定时间点的流速（弹珠速度）必须相等。

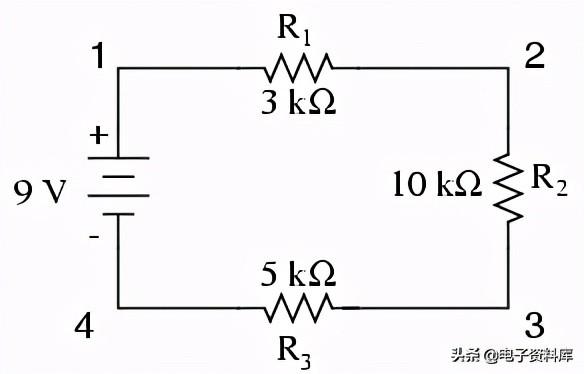
从9伏电池的排列方式，我们可以看出，电路中的电子将以逆时针方向流动，从4点到3点，再到2点到1点，再回到4点。但是，我们有一个电压源和三个电阻。我们怎么用欧姆定律呢？

对欧姆定律的一个重要警告是，所有的量（电压、电流、电阻和功率）必须在电路中的相同两点之间相互关联。例如，对于单电池、单电阻电路，我们可以轻松计算任何数量，因为它们都适用于电路中相同的两点：

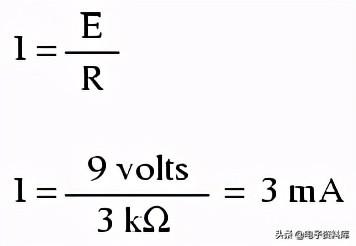
由于点1和2与电阻可忽略不计的导线连接在一起，正如点3和4一样，我们可以说点1与点2在电气上是公用的，点3与点4在电气上是公用的。因为我们知道在点1和点4之间有9伏的电动势（直接穿过电池），而且点2和点1共用，点3和点4共用，所以点2和点3之间也必须有9伏的电动势（直接穿过电阻器）。因此，我们可以将欧姆定律（I=E/R）应用于通过电阻器的电流，因为我们知道穿过电阻器的电压（E）和电阻器的电阻（R）。所有的项（E，I，R）都适用于电路中相同的两点，相同的电阻，所以我们可以毫无保留地使用欧姆定律公式。

然而，在含有一个以上电阻的电路中，我们必须小心应用欧姆定律。在下面的三电阻电路示例中，我们知道在点1和点4之间有9伏电压，这是试图推动电子通过R的串联组合的电动势的大小 one，右 two，和R three. 但是，我们不能用9伏的值除以3k，10k或5kΩ来求电流值，因为我们不知道这些电阻中的任何一个单独的电压是多少。

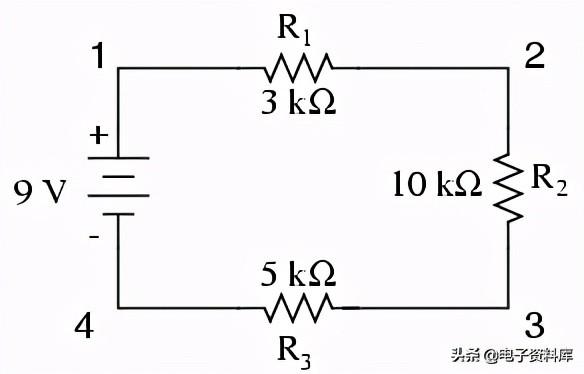
9伏的数字是全部的整个电路的数量，3k、10k、5kΩ的数字为个人单个电阻器的数量。如果我们把一个总电压的数字插入欧姆定律方程，再加上一个单独电阻的数字，结果就不会精确地与实际电路中的任何数量相关联。

对于R one，欧姆定律将关联R上的电压量 one电流通过R one，给定R one's电阻，3kΩ：

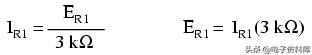
但是，因为我们不知道R的电压 one（只有通过三个电阻串联组合的电池提供的总电压）我们不知道通过R的电流 one，我们不能用这两个公式进行任何计算。R也是一样 two和R three：当且仅当电路中相同两点之间的所有项都代表其各自的量时，我们才能应用欧姆定律方程。

那我们能做什么呢？我们知道电源的电压（9伏）施加在R的串联组合上 one，右 two，和R three，我们知道每个电阻的电阻，但是由于这些电阻的大小不一样，我们不能用欧姆定律来确定电路电流。如果我们知道全部的电阻是电路的：然后我们可以计算全部的目前我们的数字是全部的voltage (I=E/R).

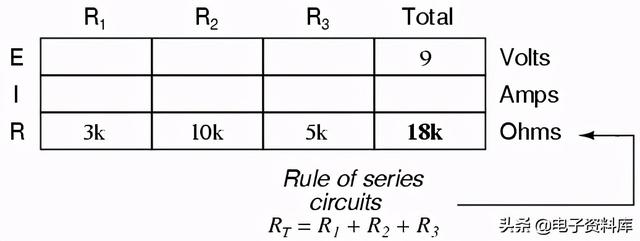
这就引出了串联电路的第二个原理：任何串联电路的总电阻等于单个电阻的总和。这应该是直观的：电子必须流过的串联电阻越多，这些电子流动的难度就越大。在示例问题中，我们串联了3 kΩ、10 kΩ和5 kΩ电阻器，总电阻为18 kΩ：

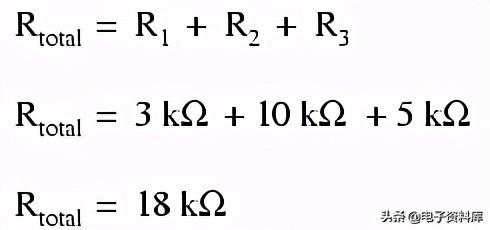
本质上，我们计算了R1的等效电阻，R2，和R3合并。知道了这一点，我们可以用一个代表R的串联组合的等效电阻重新绘制电路R1，R2，和R3 :

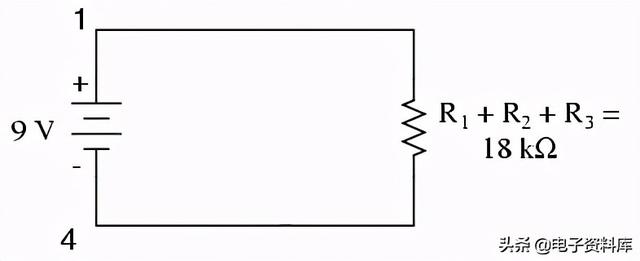
现在我们有了计算电路电流的所有必要信息，因为我们有点1和点4之间的电压（9伏）和点1和点4之间的电阻（18 kΩ）：

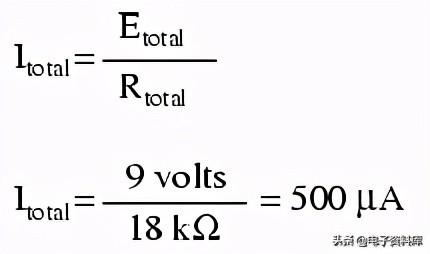
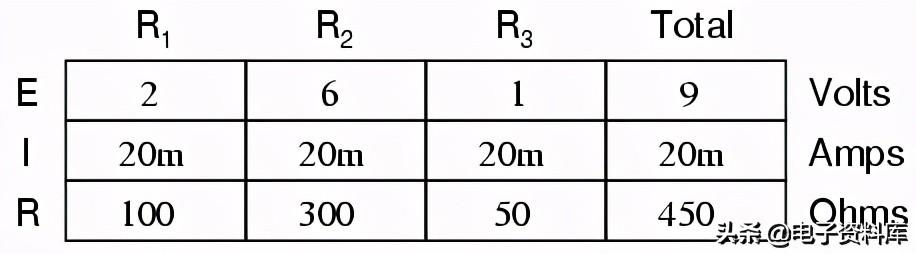
知道串联电路中所有元件的电流都是相等的（我们刚刚确定了通过电池的电流），我们可以回到原来的电路原理图，并记下通过每个元件的电流：

我们可以用欧姆定律来确定每一个电阻的欧姆定律：

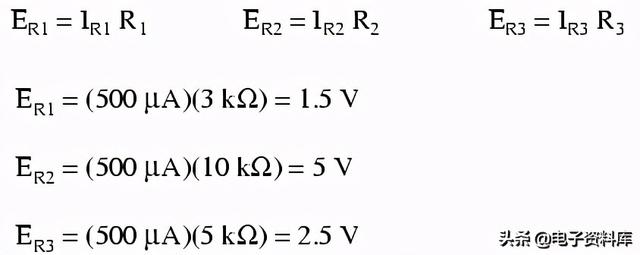
注意每个电阻器上的电压降，以及电压降的总和（1.5±2.5）如何等于蓄电池（电源）电压：9伏。这是串联电路的第三个原理：电源电压等于各个电压降的总和。

然而，我们刚刚用来分析这个简单串联电路的方法可以简化，以便更好地理解。通过使用表格列出电路中的所有电压、电流和电阻，可以很容易地看出在任何欧姆定律方程中，哪些量可以恰当地关联起来：

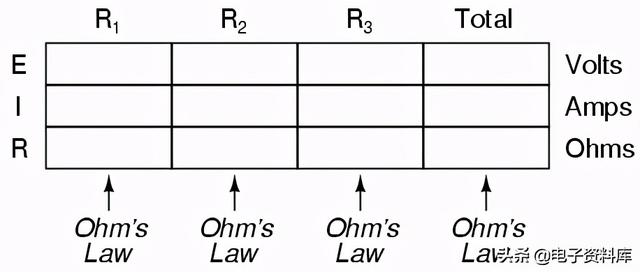
这种表格的规则是只对每个垂直列中的值应用欧姆定律。例如，ER1只有我R1和R one；ER2级只有我R2级和R two；等等。您可以通过填写表格中从头开始提供给您的元素来开始分析：

从数据的排列可以看出，我们不能用E的9伏电压T（总电压）对任何电阻（R one，右 two，或R three)在任何欧姆定律公式中，因为它们在不同的列中。蓄电池电压的9伏是不直接应用于R one，右 two，或R three. 然而，我们可以使用串联电路的“规则”来填充水平行上的空白点。在这种情况下，我们可以使用电阻的串联规则，从总和单个电阻：

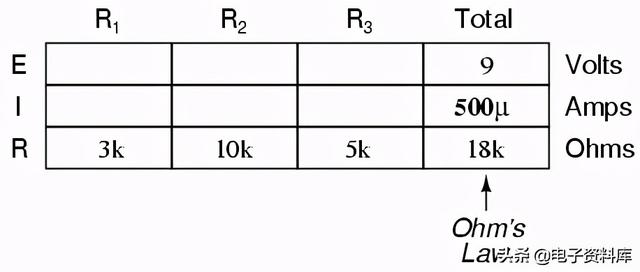
Now, with a value for total resistance inserted into the rightmost ("Total") column, we can apply Ohm's Law of I=E/R to total voltage and total resistance to arrive at a total current of 500 µA:

然后，知道电流是由串联电路的所有元件平均分配的（串联电路的另一个“规则”），我们可以根据刚刚计算出的电流值填写每个电阻器的电流：

最后，我们可以使用欧姆定律来确定每个电阻器的压降，每次一列：

为了好玩，我们可以用电脑自动分析这个电路。这将是一个很好的方法来验证我们的计算，也将变得更加熟悉计算机分析。首先，我们必须以软件可识别的格式向计算机描述电路。我们将要使用的SPICE程序要求对电路中的所有电气唯一点进行编号，并且元件的放置可以通过这些编号的点或“节点”中的哪一个共享来理解。为了清楚起见，我对示例电路1到4的四个角进行了编号。然而，SPICE要求在电路的某个地方有一个节点0，所以我将重新绘制电路，稍微更改编号方案：

我在这里所做的只是把电路的左下角重新编号为0，而不是4。现在，我可以在一个计算机文件中输入几行文本，用SPICE能理解的术语描述电路，再加上几行代码，引导程序显示电压和电流数据，以满足我们的观看乐趣。此计算机文件称为网络列表在SPICE术语中：

series circuit v1 1 0 r1 1 2 3k r2 2 3 10k r3 3 0 5k .dc v1 9 9 1 .print dc v(1,2) v(2,3) v(3,0) .end

现在，我只需运行SPICE程序来处理网络列表并输出结果：

v1 v(1,2) v(2,3) v(3) i(v1) 9.000E 00 1.500E 00 5.000E 00 2.500E 00 -5.000E-04

这个打印输出告诉我们电池电压是9伏，并且电压在R处下降 one，右 two，和R three分别为1.5伏、5伏和2.5伏。SPICE中任何元件上的电压降都是由元件之间的节点号来引用的，因此v（1,2）是指电路中节点1和节点2之间的电压，这两个节点之间的R one位于。节点号的顺序很重要：当SPICE输出v（1,2）的数字时，它对待极性的方式与我们拿着电压表的方式相同，电压表的红色测试引线在节点1上，黑色测试引线在节点2上。

我们也有一个显示0.5毫安或500微安的电流（尽管是负值）。所以我们的数学分析已经被计算机证明是正确的。这个数字在SPICE分析中显示为负数，这是因为SPICE处理当前计算的方式有点古怪。

总之，串联电路被定义为只有一个电子流动路径。根据这个定义，串联电路遵循三条规则：所有元件共享相同的电流；电阻加起来等于更大的总电阻；电压降加起来等于更大的总电压。所有这些规则都源于串联电路的定义。如果你完全理解这个定义，那么这些规则只不过是定义的脚注而已。

• 回顾：
• 串联电路中的元件共享相同的电流：I总计= I one= I two= . . . In
• 串联电路中的总电阻等于各电阻之和：R总计= R oneR two. . . Rn
• 串联电路中的总电压等于各个电压降的总和：E总计= E oneE two. . . En

简单并联电路

让我们从一个由三个电阻和一个电池组成的并联电路开始：

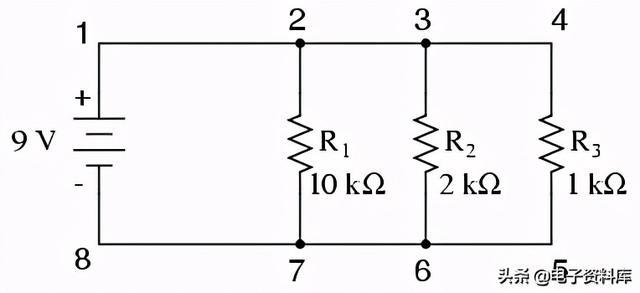
了解并联电路的第一个原则是电路中所有元件的电压相等。这是因为在一个并联电路中只有两组电气公共点，在任何给定时间，两组公共点之间测得的电压必须始终相同。因此，在上述电路中，R one等于R上的电压 two等于R上的电压 three等于电池的电压。电压相等可以在另一个表中表示为起始值：

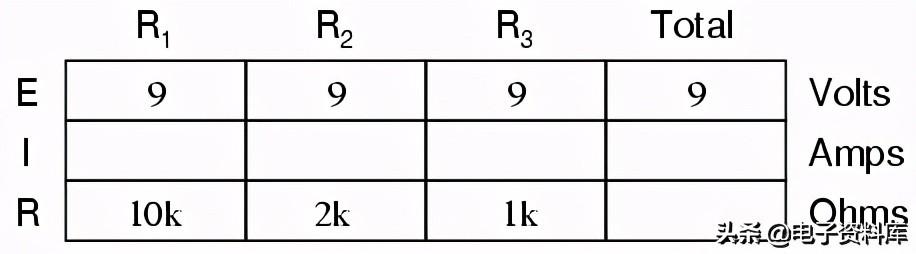
就像串联电路的情况一样，欧姆定律同样需要注意：电压、电流和电阻的值必须在相同的背景下才能正确计算。然而，在上面的示例电路中，我们可以立即对每个电阻器应用欧姆定律，以找到其电流，因为我们知道每个电阻器的电压（9伏）和每个电阻器的电阻：

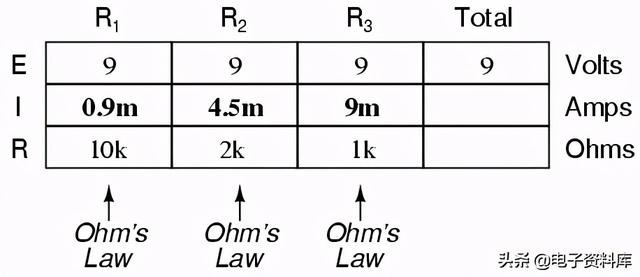
在这一点上，我们仍然不知道这个并联电路的总电流或总电阻是多少，所以我们不能将欧姆定律应用到最右边的（“总”）列。但是，如果我们仔细考虑正在发生的事情，那么很明显，总电流必须等于所有单个电阻器（“支路”）电流的总和：

当总电流在8点从蓄电池负极（-）端子流出并流经电路时，部分电流在7点分流，通过R向上流动 one，更多的在6点分开，通过R向上 two，余数通过R向上 three. 就像一条河流分为几条小河，所有溪流的总流量必须等于整条河的流量。当电流通过R one，右 two，和R three连接以流回电池正极端子（）朝向点1：从点2到点1的电子流必须等于通过R的（支路）电流之和 one，右 two，和R three .

这是并联电路的第二个原理：电路总电流等于各支路电流之和。利用这个原理，我们可以填写IT在我们的桌子上点上我的总数R1，我R2级，我呢第3页 :

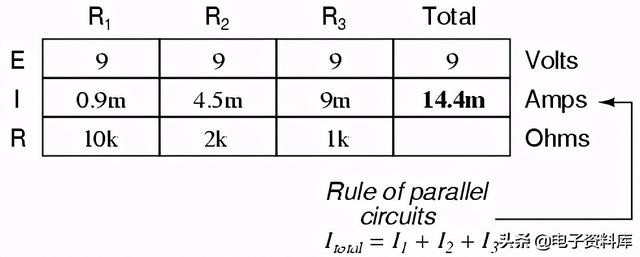
最后，将欧姆定律应用到最右边（“总计”）列，我们可以计算总电路电阻：

请注意一些非常重要的事情。电路总电阻只有625Ω：较少的比任何一个单独的电阻。总电阻是电路的总电阻更大的比任何一个单独的电阻。然而，在并联电路中，情况恰恰相反：我们说单个电阻减少而不是添加算出总数。这一原理完善了我们对并联电路的“规则”三元组，就像串联电路被发现有电压、电流和电阻三个规则一样。从数学上讲，并联电路中总电阻和单个电阻之间的关系如下所示：

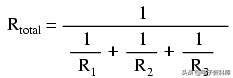
同样的基本方程形式适用于任何并联连接在一起的电阻数，只需在分数的分母上添加尽可能多的1/R项，以容纳电路中的所有并联电阻。

就像串联电路一样，我们可以用计算机分析来复查我们的计算。当然，首先，我们必须用计算机能理解的术语来描述我们的示例电路。我将从重新绘制电路开始：

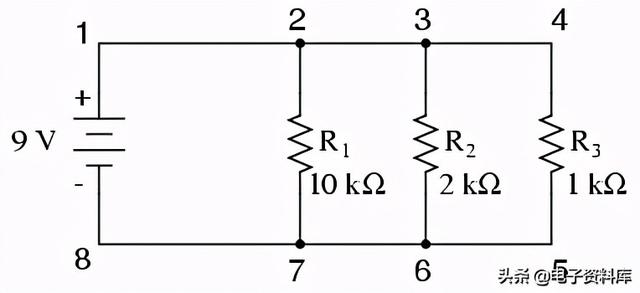
我们再一次发现，为了SPICE的利益，用于识别电路中点的原始编号方案将不得不改变。所有的SPICE节点必须共享相同的点。这就是SPICE如何知道什么和什么以及如何联系在一起的。在一个简单的并联电路中，所有的点在两组点中的一组中都是电共有的。对于我们的示例电路，连接所有组件顶部的导线将具有一个节点号，而连接组件底部的导线将具有另一个节点号。遵循将零作为节点号的惯例，我选择0和1：

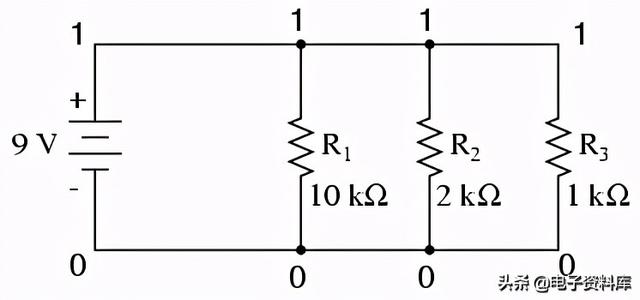
这样的一个例子使SPICE中节点编号的基本原理非常清楚。通过让所有的组件共享一组数字，计算机“知道”它们都是并行连接的。

我们需要在这些源中插入电流源的零电压，然后把这些电流源插入到基准线中。不管出于什么原因，SPICE程序的创造者使它只能计算电流通过电压源。这是一个有点恼人的SPICE模拟程序需求。添加这些“虚拟”电压源后，必须创建一些新的节点编号，以将它们连接到各自的分支电阻器：

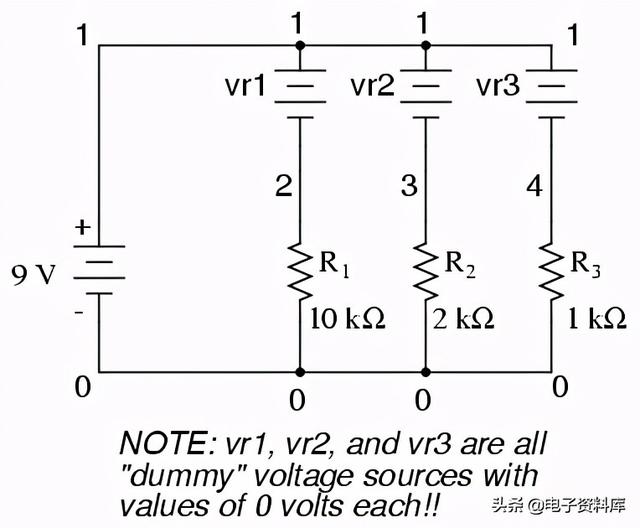
虚拟电压源均设置为0伏，以便不会影响电路的运行。电路描述文件，或网络列表，如下所示：

Parallel circuit v1 1 0 r1 2 0 10k r2 3 0 2k r3 4 0 1k vr1 1 2 dc 0 vr2 1 3 dc 0 vr3 1 4 dc 0 .dc v1 9 9 1 .print dc v(2,0) v(3,0) v(4,0) .print dc i(vr1) i(vr2) i(vr3) .end

运行计算机分析，我们得到以下结果（我用描述性标签对打印输出进行了注释）：

v1 v(2) v(3) v(4) 9.000E 00 9.000E 00 9.000E 00 9.000E 00 battery R1 voltage R2 voltage R3 voltage voltage

v1 i(vr1) i(vr2) i(vr3) 9.000E 00 9.000E-04 4.500E-03 9.000E-03 battery R1 current R2 current R3 current voltage

这些值确实与先前通过欧姆定律计算得出的值相匹配：0.9毫安R1，I为4.5毫安R2级，9毫安第3页. 当然，由于并联连接，所有电阻的压降都是相同的（9伏，与电池相同）。

总之，并联电路是指所有元件都连接在同一组电气公共点之间的电路。另一种说法是，所有组件都通过彼此的终端进行连接。根据这个定义，并联电路遵循三条规则：所有元件共享相同的电压；电阻减小等于较小的总电阻；支路电流增加等于较大的总电流。就像串联电路一样，所有这些规则都来源于并联电路的定义。如果你完全理解这个定义，那么这些规则只不过是定义的脚注而已。

• 回顾：
• 并联电路中的元件共享相同的电压：E总计= E one= E two= . . . En
• 并联电路中的总电阻为较少的比任何一个单独的阻力：R总计= 1 / (1/R one1/R型 two. . . 1/R型n )
• 并联电路中的总电流等于各支路电流之和：I总计= I one我 two. . . 我n .

电导

当学生们第一次看到平行阻力方程时，自然要问的问题是，“在哪里那个东西是从哪里来的？”这确实是一个奇怪的算术，它的起源值得一个很好的解释。

根据定义，阻力是摩擦一个组件呈现出电子通过它的流动。电阻用大写字母“R”表示，以“欧姆”为单位进行测量。然而，我们也可以用它的倒数来考虑这种电特性：如何容易的它是让电子流过元件，而不是如何流动困难的. 如果抵抗我们用这个词来表示电子流动有多困难，然后用这个词来表示电子流动有多容易电导 .

从数学上讲，电导是电阻的倒数：

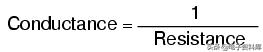
电阻越大，电导越小，反之亦然。这应该是直观的，电阻和电导是相反的方式来表示相同的基本电性质。如果比较两个组件的电阻，发现组件“A”的电阻是组件“B”的一半，那么我们可以通过说组件“A”是两次和元件“B”一样导电。如果元件“A”的电阻只有元件“B”的三分之一，那么我们可以说它是三次比元件“B”更导电，以此类推。

更进一步，一个符号和单位被创造来代表电导。符号是大写字母“G”，单位是mho，这是“ohm”的反拼写（你不认为电子工程师有任何幽默感！）。尽管它是适当的，但在以后的几年里，mho的单位被西门子（缩写为大写字母“S”）。这个改变单位名称的决定让人想起温度单位度的变化摄氏度度摄氏度或频率单位的变化c、 p.s（每秒循环数）到赫兹. 如果你在这里寻找一个模式，西门子、Celsius和Hertz都是著名科学家的姓氏，遗憾的是，这些姓氏告诉我们的并不是单元的原始名称，而是单元的性质。

作为一个脚注，西门子的单位永远不会没有最后一个字母“s”。换言之，没有“siemen”的单位是“ohm”或“mho”的单位。这是因为各科学家的姓氏拼写正确。电阻的单位是以一个叫“欧姆”的人命名的，而电导的单位是以一个叫“西门子”的人命名的，因此将后者“单数化”是不恰当的，因为它的最后一个“s”并不表示复数。

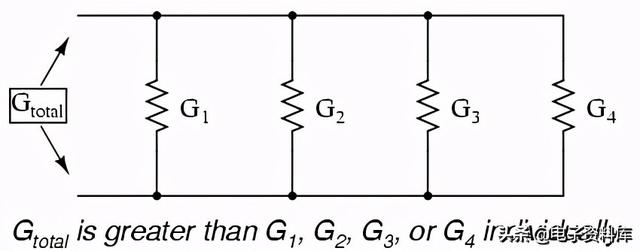
回到我们的并联电路例子，我们应该可以看到电流的多路径（支路）会降低整个电路的总电阻，因为电子能够更容易地流过多个支路的整个网络，而不是单独通过这些支路电阻中的任何一个。依据抵抗，额外的分支会导致较小的总数（当前遇到的阻力较小）。依据电导但是，额外的分支会导致更大的总量（电子流的电导更大）：

总并联电阻为较少的比任何一个单独的支路电阻都要小，因为并联电阻的电阻比它们单独的电阻要小：

总并联电导为更大的因为并联电阻在一起比单独使用要好：

更准确地说，并联电路中的总电导等于各电导之和：

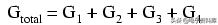
如果我们知道电导只不过是电阻的数学倒数（1/x），我们可以通过将每个电导的倒数代入，将上述公式中的每一项转化为电阻：

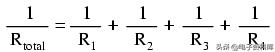
通过求解上述总阻力方程（而不是总阻力的倒数），我们可以反转（倒换）方程的两边：

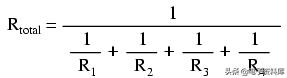
所以，我们终于得出了神秘的阻力公式！电导（G）很少被用作实际测量，因此上述公式是并联电路分析中常见的公式。

• 回顾：
• 电导与电阻相反：如何测量容易的它是为了让电子流过某物。
• 电导用字母“G”表示，用单位为mhos或西门子 .
• 从数学上讲，电导等于电阻的倒数：G=1/R。

功率计算

在计算电阻元件的功耗时，使用三个功率方程中的任何一个，从每个元件的电压、电流和/或电阻值中得出答案：

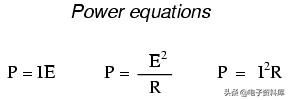
这很容易通过在我们熟悉的电压、电流和电阻表中添加另一行来管理：

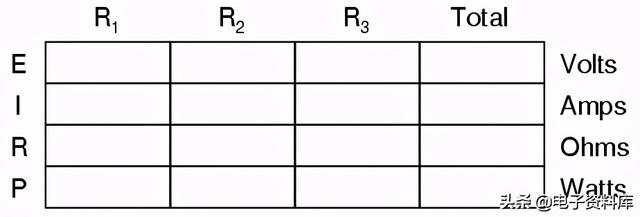
任何特定表格列的功率都可以通过适当的欧姆定律方程求出(适当的根据该列中E、I和R的数据）。

总功率与单个功率的一个有趣的规则是，它对于任何电路配置：串联、并联、串联/并联或其他。功率是衡量工作效率的一个指标，而且由于功率耗散必须等于电源施加的总功率（根据物理能量守恒定律），电路配置对数学没有影响。

• 回顾：
• 权力在任何电阻电路配置：P总计= P oneP two. . . Pn

欧姆定律的正确使用

电子学初级学生在应用欧姆定律时最常犯的错误之一是混合了电压、电流和电阻的背景。换言之，学生可能会错误地使用一个电阻的I值和穿过一组互连电阻的E值，以为它们会得到这一个电阻的电阻值。不是这样！记住这条重要的规则：欧姆定律方程中使用的变量必须是常见的在考虑中的电路中相同的两点。这条规则我怎么强调也不过分。在串并联组合电路中，这一点尤为重要，因为相邻元件的两个压降值可能不同和电流

当使用欧姆定律计算一个与单个元件有关的变量时，请确保您所参考的电压仅穿过该单一元件，您所参考的电流仅通过该单一元件，而您所参考的电阻仅适用于该单一元件。同样，当计算与电路中的一组元件有关的变量时，请确保电压、电流和电阻值仅特定于该整套元件！记住这一点的一个好方法是密切注意两点终止被分析的元件或元件组，确保有问题的电压穿过这两个点，所讨论的电流是从其中一个点一直流到另一个点，所讨论的电阻相当于这两个点之间的一个电阻，并且所讨论的功率是这两点之间所有部件消耗的总功率。

本章中提出的串联和并联电路的“表”法是一种很好的方法，可以使欧姆定律的上下文对于任何类型的电路配置都是正确的。在如下所示的表格中，只允许对单个值应用欧姆定律方程垂直的一次列：

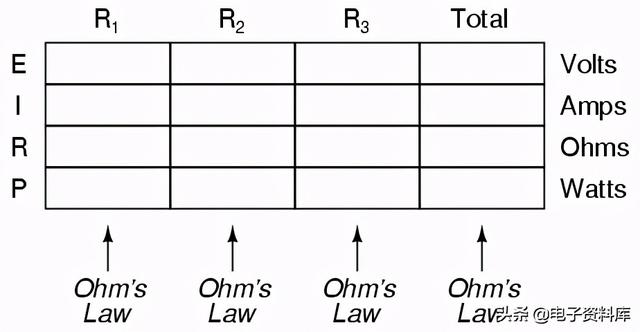
推导值水平根据串联和并联电路的原理，允许跨列：

“表”法不仅简化了对所有相关量的管理，还便于通过其他方法求解原始未知变量，或通过反向工作从解中求解初始给定值，从而方便交叉检查答案。例如，如果您刚刚解决了电路中所有未知的电压、电流和电阻，则可以通过在底部添加一行来检查您的工作，以计算每个电阻器的功率，看看是否所有单独的功率值加起来等于总功率。如果没有，那你一定是在什么地方犯了错误！虽然这种“交叉检查”技术并不新鲜，但是使用表来安排交叉检查的所有数据会导致最少的混乱。

• 回顾：
• 将欧姆定律应用于表中的垂直列。
• 对表中的水平行应用串联/平行规则。
• 检查你的计算，通过“反向”工作，试图得到最初给定的值（从你第一次计算的答案），或通过求解一个数量使用一个以上的方法（从不同的给定值）。

部件失效分析

技术人员的工作经常涉及到故障电路的“故障排除”（定位和纠正问题）。良好的故障排除是一项要求很高且有回报的工作，需要对基本概念有透彻的理解，有能力提出假设（对某一影响的拟议解释），能够根据其概率判断不同假设的价值（一个特定的原因比另一个原因的可能性有多大），以及运用解决方案解决问题的创造力。虽然将这些技能提炼成科学的方法论是可能的，但大多数有经验的故障排除人员都会同意，故障排除涉及到艺术的一点，并且需要多年的经验才能充分发展这门艺术。

必须具备的一项基本技能是对元件故障如何影响不同配置的电路有一个现成和直观的理解。我们将在这里探讨串联和并联电路中元件故障的一些影响，然后在“串联-并联组合电路”一章的结尾处进行更大程度的探讨。

让我们从一个简单的串联电路开始：

当电路中的所有元件都在其正确的值下工作时，我们可以从数学上确定所有电流和电压降：

现在让我们假设R2故障短路短路这意味着电阻现在就像一根直线，几乎没有电阻。电路将表现得像一根跨接导线跨接在R2上（如果您想知道，“跨接导线”是电路中临时导线连接的常用术语）。是什么原因导致R2短路，在这个例子中，我们只关心它对电路的影响：

带R2通过跨接导线或内部电阻器故障短路，总电路电阻将减少. 由于电池输出的电压是恒定的（至少在我们的理想模拟中是这样），总电路电阻的减小意味着总电路电流必须增加 :

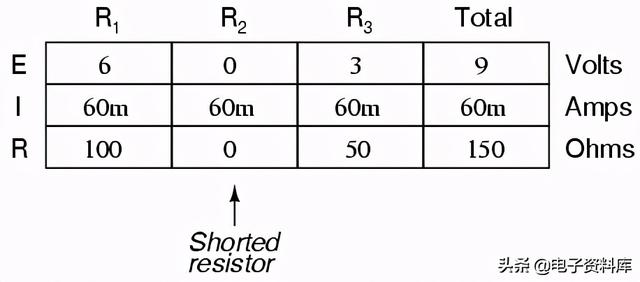
当电路电流从20毫安增加到60毫安时，R1端的电压下降和R3（没有改变电阻）也增加了，所以两个电阻下降了整整9伏。R2被跨接导线的极低电阻旁路，有效地从电路中消除，从一根引线到另一根引线的电阻已降至零。因此，R2上的电压降，即使总电流增加，也是零伏。

另一方面，如果R2如果发生故障“开路”——电阻增加到几乎无限大的水平——它也会在电路的其他部分产生广泛的影响：

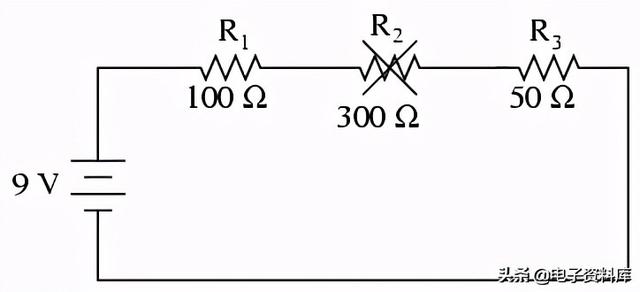
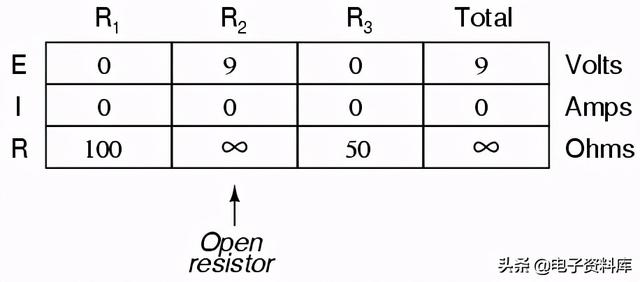
带R2在无穷大电阻和总电阻等于串联电路中所有单个电阻之和时，总电流减小为零。当电路电流为零时，没有电子流在R1或R3上产生电压降. R2另一方面，将显示其端子上的全部电源电压。

我们也可以将相同的前/后分析技术应用于并行电路。首先，我们确定一个“健康”的并联电路应该是什么样的。

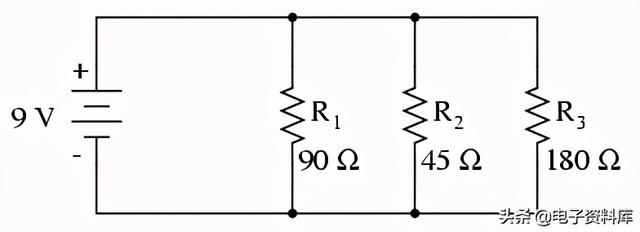
假设R2在这个并联电路中开路，其影响如下：

请注意，在这个并联电路中，开路的支路只影响通过该支路的电流和电路的总电流。总电压——在并联电路的所有元件上平均分配，对所有电阻来说都是一样的。由于电压源倾向于保持电压常数所有的电阻都会和之前的电压保持一致。由于电压是并联电路中唯一的公共参数，而其他电阻的电阻值没有改变，因此它们各自的支路电流保持不变。

这就是在家用灯电路中发生的事情：所有的灯都从并联的电源线获得工作电压。打开和关闭一盏灯（该并联电路中的一个支路闭合和断开）不影响室内其他灯具的工作，只影响该灯（支路）中的电流和为房间内所有灯具供电的总电流：

在理想情况下（有完美的电压源和零电阻连接线），一个简单的并联电路中的电阻短路也不会对电路的其他分支产生影响。在现实生活中，效果并不完全相同，我们将在下面的示例中了解原因：

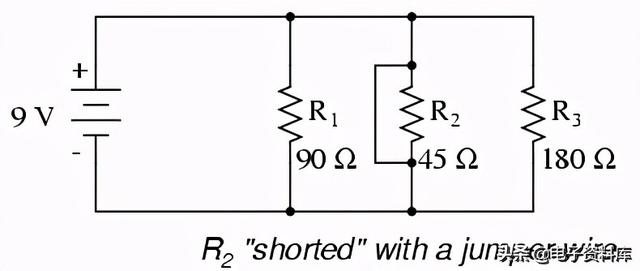
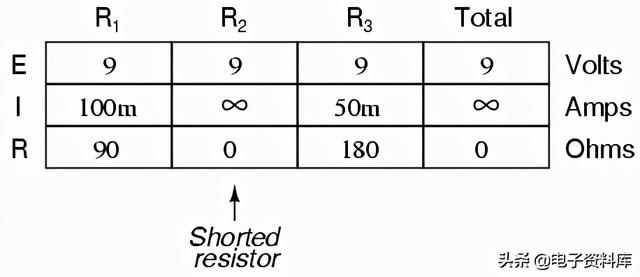
短路电阻器（电阻为0Ω）理论上会从任何有限的电压源（I=E/0）中吸取无穷大的电流。在这种情况下，R2的零电阻将电路总电阻也减小到0Ω，将总电流增加到无穷大。但是，只要电压源保持稳定在9伏，其他支路电流（IR1我呢第3页)将保持不变

然而，在这个“完美”的方案中，关键的假设是：当向短路负载提供无限量的电流时，电压供应将在其额定电压下保持稳定。这根本不现实。即使短路电阻很小（相对于绝对零电阻），也不会真实的电压源可以任意提供大的过载电流，同时保持电压稳定。这主要是由于所有电源固有的内阻，这是由它们构成的材料不可避免的物理特性造成的：

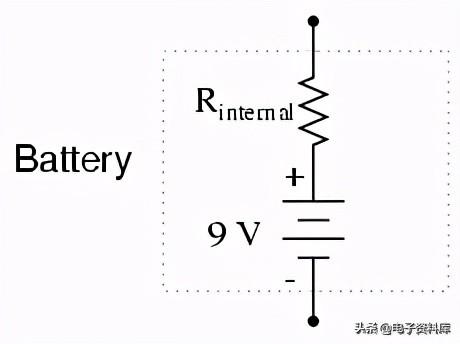
这些电阻可以变成一个简单的串联并联电路。通常，电压源的内阻很低，可以安全地忽略，但是当遇到由短路元件引起的高电流时，它们的影响变得非常明显。在这种情况下，短路的R two会导致几乎所有的电压都通过电池的内阻下降，而电阻R几乎没有剩余的电压 one，右 two，和R three :

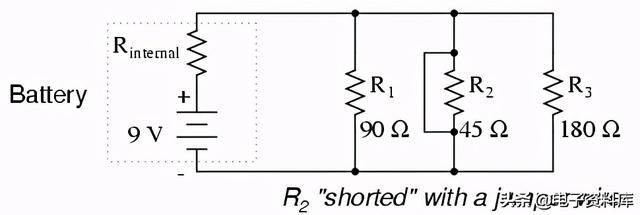
可以说，故意在任何电压源的端子上直接短路都是个坏主意。即使产生的高电流（热、闪光、火花）不会对附近的人造成伤害，电压源也可能会受到损害，除非它专门设计用于处理短路，而大多数电压源并非如此。

最后在这本书中，我将引导你通过电路分析不用任何数字也就是说，在不知道电池产生多少伏电压、每个电阻器的电阻有多少欧姆的情况下，分析电路中元件故障的影响。本节作为此类分析的入门步骤。

而欧姆定律和串并联电路规则的正常应用是用数值量来完成的(“定量”)，这种新的分析没有精确的数字，我喜欢称之为定性的分析。换句话说，我们将分析品质而不是精确的量. 结果，对你来说，将是一个更深刻的直观理解电路操作。

• 回顾：
• 为了确定如果某个元件发生故障，电路中会发生什么情况，用故障元件的等效电阻重新绘制电路，然后重新计算所有值。
• 直观地确定电路中任何给定元件故障会发生什么的能力是关键的任何电子故障检修人员的技能发展。最好的学习方法是用电路计算和实际电路做实验，密切注意什么会随着故障而改变，什么保持不变，以及为什么？ !
• A短路组件的电阻急剧下降
• 安打开组件的电阻急剧增加。根据记录，电阻器往往比故障短路更容易发生故障断开，而且除非物理或电气压力过大（物理上滥用或过热），否则它们几乎从不发生故障。

建造简单的电阻电路

在学习电学的过程中，你会想用电阻和电池来构造你自己的电路。在电路装配方面，有些选项是可用的，有些比其他的更容易。在本节中，我将探讨两种制造技术，这些技术不仅有助于您构建本章中所示的电路，还将帮助您构建更高级的电路。

如果我们只想构造一个简单的单电池、单电阻电路，我们可以很容易地使用鳄鱼夹像这样的跨接导线：

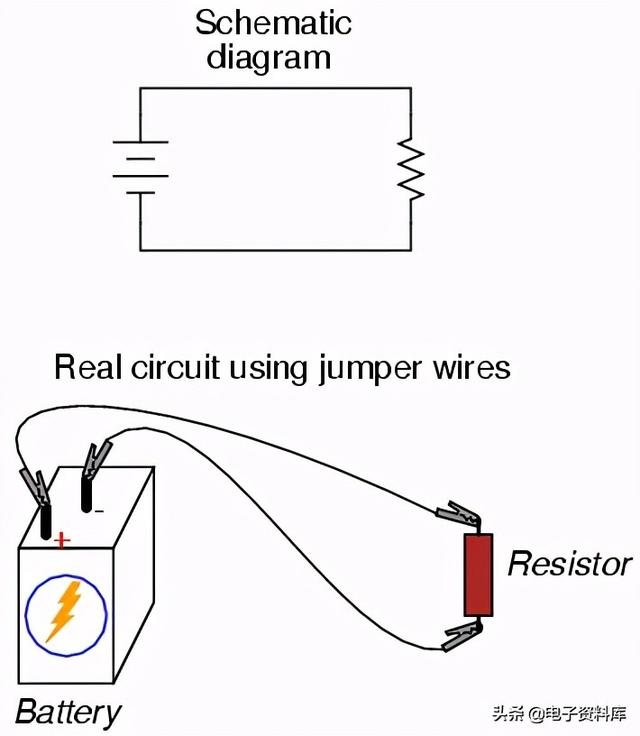
两端带有“鳄鱼”式弹簧夹的跨接导线提供了一种安全方便的电气连接部件的方法。

如果我们想用一个电池和三个电阻构建一个简单的串联电路，同样的使用跨接导线的“点对点”构造技术可以应用：

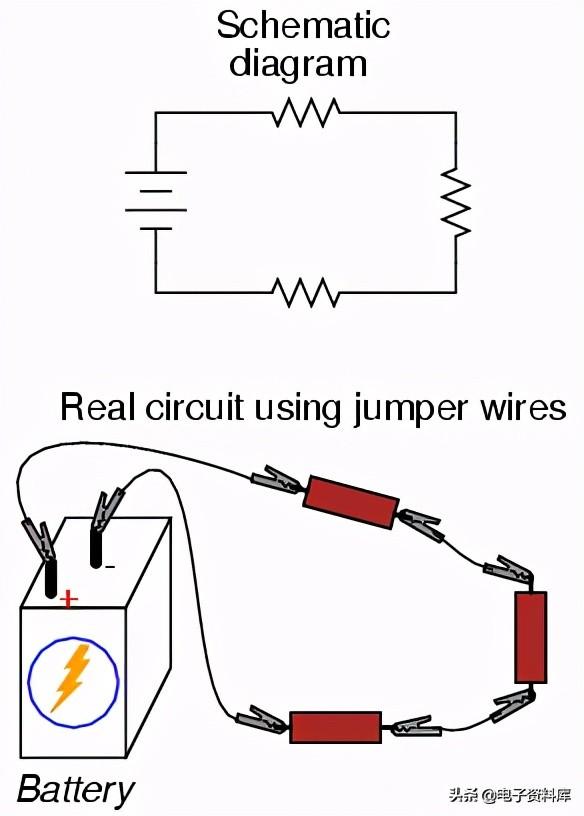
然而，由于跨接导线的笨拙和连接的物理脆弱性，这种技术对于比这复杂得多的电路来说是不切实际的。业余爱好者更常见的临时施工方法是无焊试验板，一种由塑料制成的装置，带有数百个弹簧加载的连接插座，连接组件和/或22号实心线件的插入端。这里显示了一张真实的试验板的照片，后面的插图显示了一个简单的串联电路：

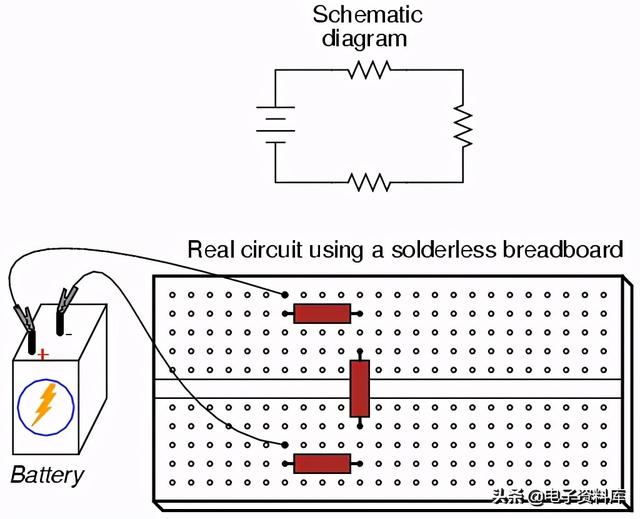
在试验板表面的每个孔下面都有一个金属弹簧夹，用来抓住任何插入的导线或元件导线。这些金属弹簧夹连接在试验板表面下面，使插入的导线之间连接起来。连接方式沿垂直柱每隔五个孔连接（如所示，试验板的长轴水平放置）：

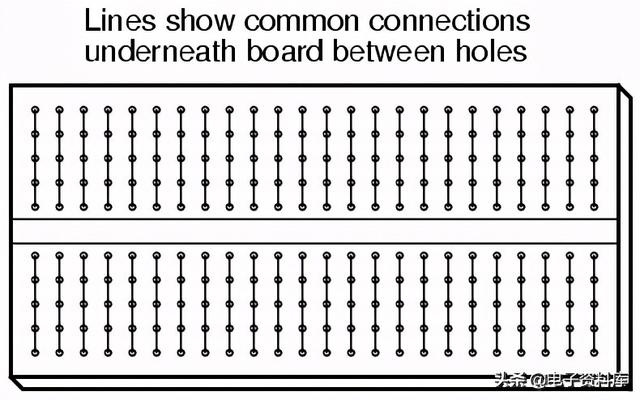
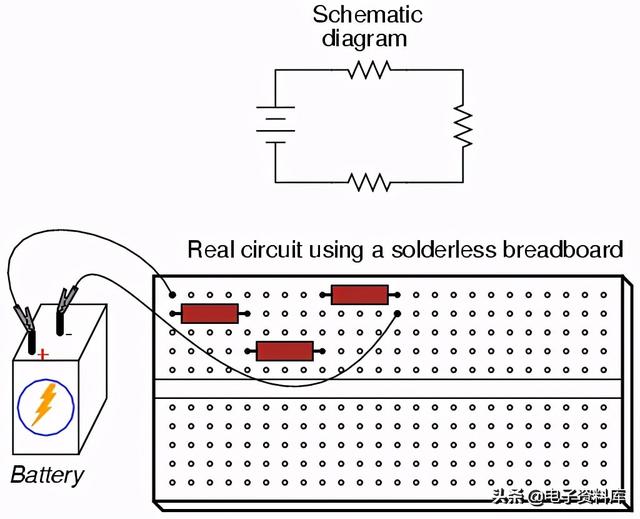
因此，当导线或元件引线插入试验板上的孔时，该列中还有四个孔为其他导线和/或元件引线提供潜在的连接点。其结果是为建造临时电路提供了一个非常灵活的平台。例如，刚刚显示的三电阻电路也可以建立在这样的试验板上：

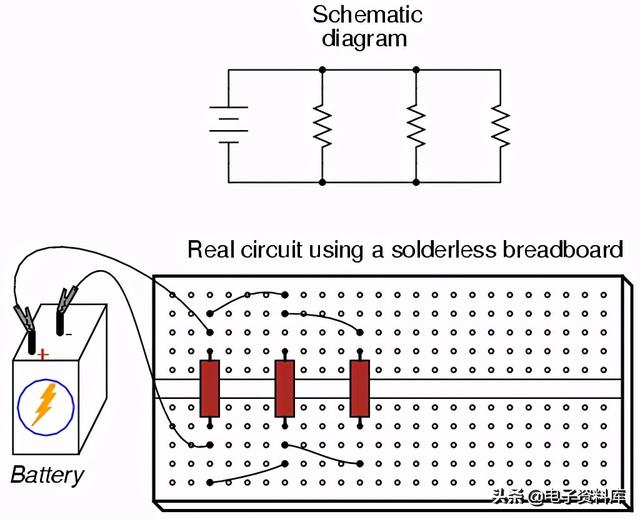
并联电路也很容易在无焊试验板上构建：

不过，面包板也有其局限性。首先，它们是为了暂时的仅限施工。如果你拿起一块试验板，把它翻过来，然后摇晃它，任何插入它的部件都会松动，并可能从它们各自的孔中掉出来。此外，试验板仅限于相当低电流（小于1安培）的电路。这些弹簧夹的接触面积很小，因此在没有过度加热的情况下无法支持高电流。

为了更持久，人们可能希望选择焊接或电线包装。这些技术包括将组件和电线固定到提供安全机械位置的某些结构上（例如在其上钻有孔的酚醛或玻璃纤维板，很像没有固有弹簧夹连接的试验板），然后将电线连接到固定的部件引线上。焊接是低温焊接的一种形式，使用锡/铅或锡/银合金熔化和电粘合铜物体。焊接到元件引线或连接到电路板表面的小铜环“垫”上的导线端用于将元件连接在一起。在绕线中，一根小规格的导线紧紧地缠绕在元件导线上，而不是焊接在导线或铜垫上，绕包导线的张力提供了一个良好的机械和电气连接，将元件连接在一起。

一个示例印刷电路板，或印刷电路板，供业余爱好者使用，如图所示：

这块板是铜质的一面朝上：所有焊接都完成的那一面。每个孔周围都有一层小铜金属，用于焊接。在这个特殊的电路板上，所有的孔都是相互独立的，不像无焊试验板上的孔是五个一组连接在一起的。不过，可以购买与试验板相同的5孔连接模式的印刷电路板，并将其用于爱好电路建设。

生产印刷电路板有踪迹在酚醛或玻璃纤维基材上形成预先设计好的连接通道的铜，在电路中起到电线的作用。这里展示了这样一个电路板的一个例子，这个装置实际上是一个“电源”电路，它被设计成从家用壁挂式插座获得120伏交流电（AC）并将其转换成低压直流电（DC）。一个电阻出现在这个电路板上，从底部开始计数的第五个元件，位于电路板的右中部。

从这个板的下面可以看到连接组件的铜“痕迹”，以及连接部件的银白色焊料沉积物

焊接或绕线电路被认为是永久性的：也就是说，它不太可能意外地分崩离析。然而，有时也会考虑这些施工技术太永久的。如果有人想更换元件或以任何实质性的方式改变电路，他们必须花相当长的时间来断开连接。此外，焊接和绕线都需要专门的工具，这些工具可能无法立即获得。

在工业世界中使用的另一种施工技术是端子排. 端子排，也称为隔离带或接线端子，由一段不导电的材料和嵌入其中的几个小金属棒组成。每根金属棒至少有一个机械螺钉或其他紧固件，可在其下固定导线或元件引线。由一个螺钉固定的多条导线在电气上相互通用，同一根杆上固定在多个螺钉上的导线也一样。下图显示了一种类型的端子排，其中连接了一些导线。

另一个更小的端子排如下图所示。这种类型，有时被称为“欧式”样式，有凹入式螺钉，有助于防止螺丝刀或其他金属物体造成端子之间的意外短路：

在下图中，一个单电池，三个电阻电路构成在一个端子板上：

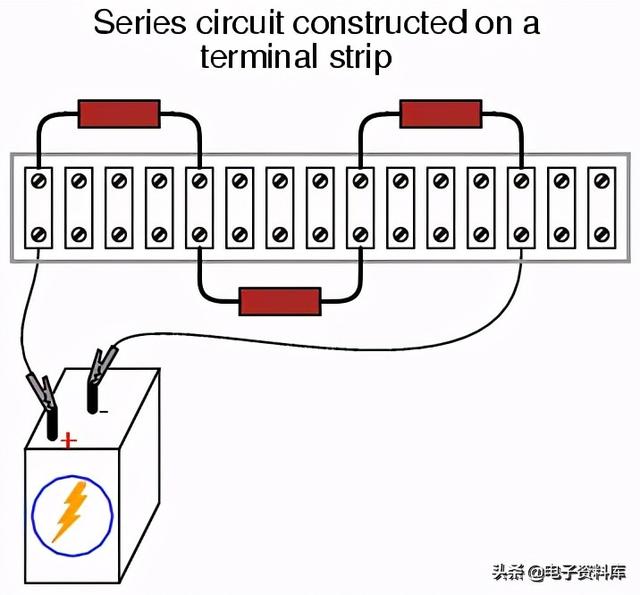
如果端子板使用机器螺钉固定部件和电线端部，则只需螺丝刀即可固定新连接或断开旧连接。有些端子板使用弹簧夹——类似于试验板，只是增加了耐用性——使用螺丝刀作为推动工具接合和分离（不涉及扭曲）。由接线板建立的电气连接相当牢固，并且被认为适合永久性和临时性施工。

任何人对电路原理图和实际电路图都不感兴趣。通常绘制示意图是为了最大程度地提高可读性（除了那些为制造最大混乱而绘制的值得注意的示例！）但实际的电路结构通常需要不同的元件方向。在端子排上建立简单的电路是发展空间推理技能的一种方法，即“拉伸”导线以形成相同的连接路径。考虑一个单电池的情况，三个电阻并联电路构建在一个接线板上：

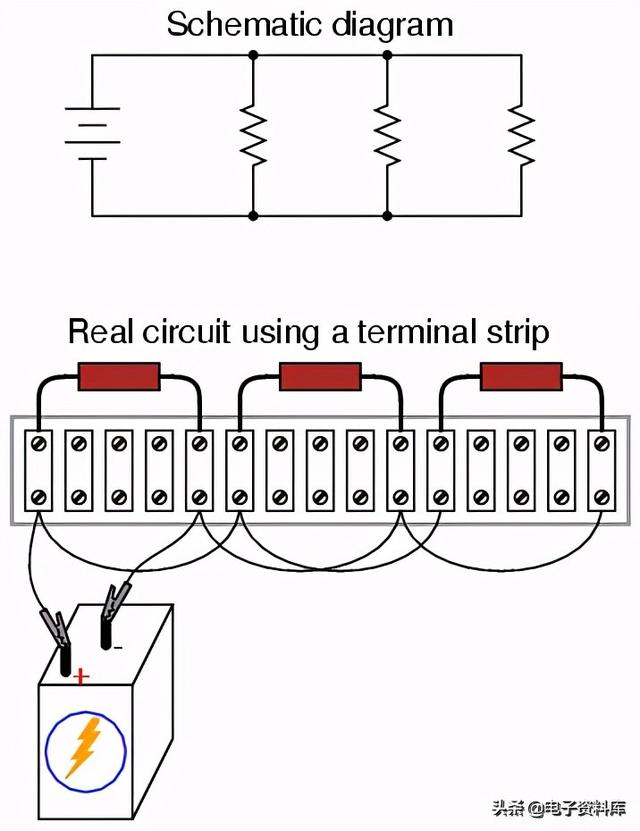
从一个漂亮、整洁的原理图发展到真正的电路——特别是当要连接的电阻器被物理地安排在线性的端子排上的时尚——对很多人来说并不明显，所以我将一步一步地概述这个过程。首先，从干净的原理图开始，将所有部件固定到端子排上，不要使用连接线：

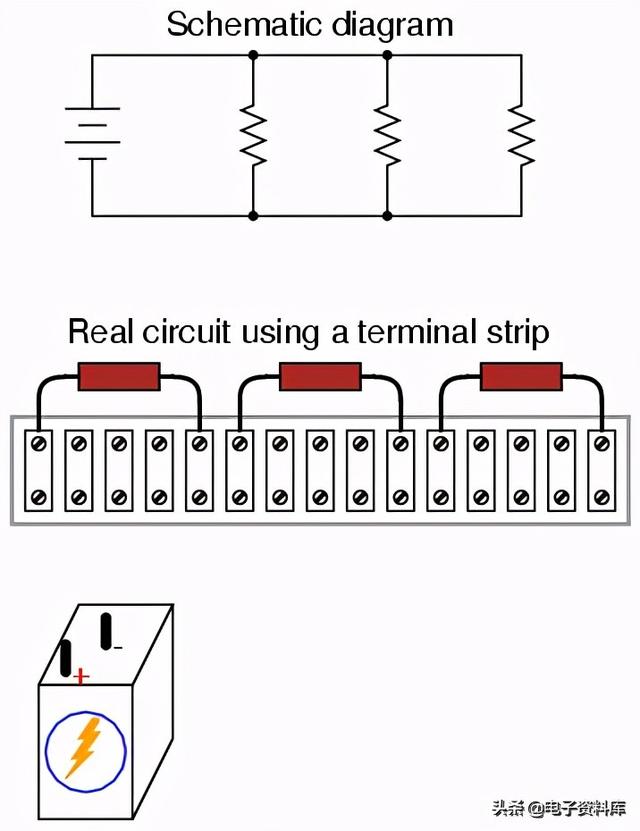
接下来，追踪从蓄电池一侧到示意图中第一个元件的导线连接，在实际电路的相同两点之间固定一根连接导线。我发现用另一条线来画示意图的线是很有帮助的，以表明我在现实生活中所做的连接：

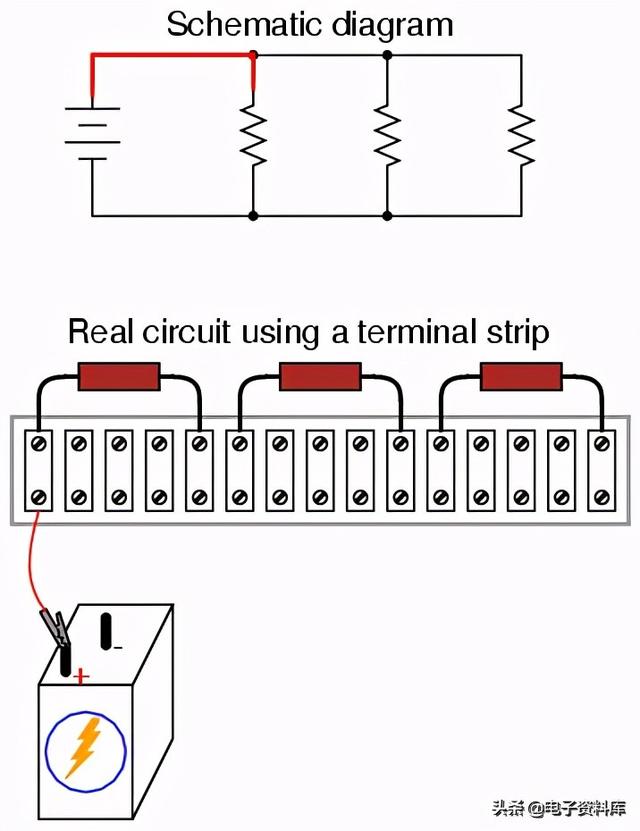
继续这一过程，逐线进行，直到示意图中的所有连接都已说明。以一种类似香料的方式来看待公共线可能会很有帮助：将电路中所有到公共线的连接都作为一个步骤，确保每个连接到该线的组件在继续下一个连接之前实际上都已连接到该线。在下一步中，我将展示其余两个电阻器的顶部是如何连接在一起的，与上一步中固定的导线相同：

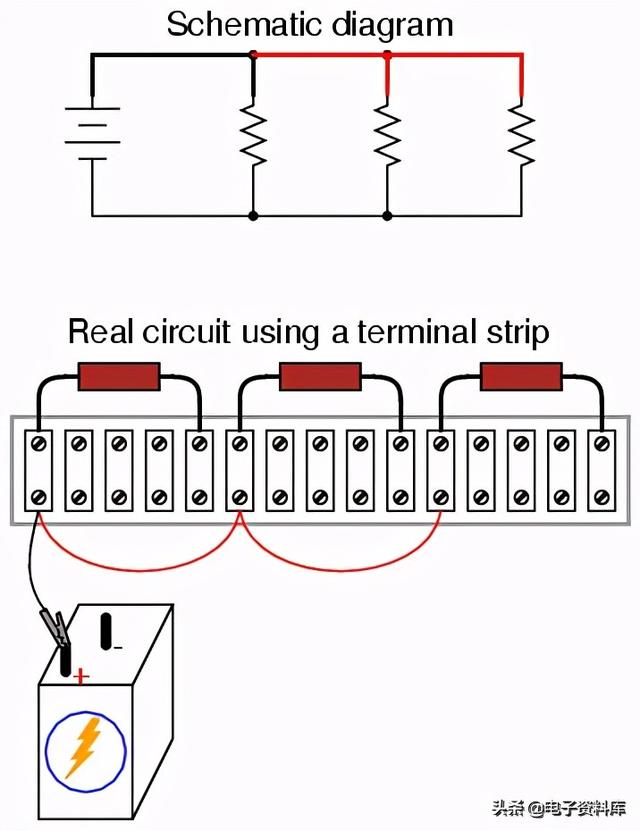
将所有电阻器的顶部（如示意图所示）连接在一起，并连接到蓄电池的正极（）端子，我们现在要做的就是将底部连接在一起并连接到蓄电池的另一侧：

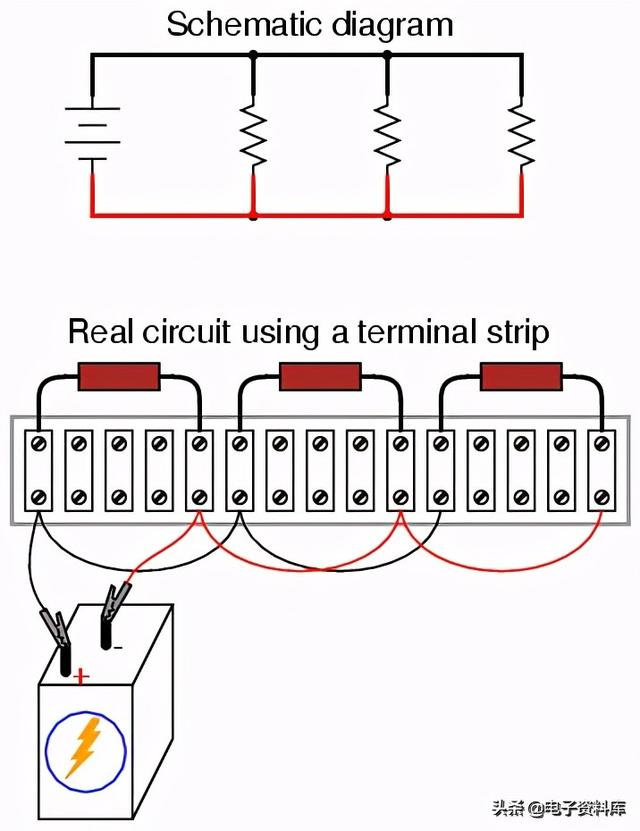
通常在工业中，所有导线都用编号标记进行标记，电气通用导线具有相同的位号，就像在SPICE模拟中一样。在这种情况下，我们可以标记电线1和2：

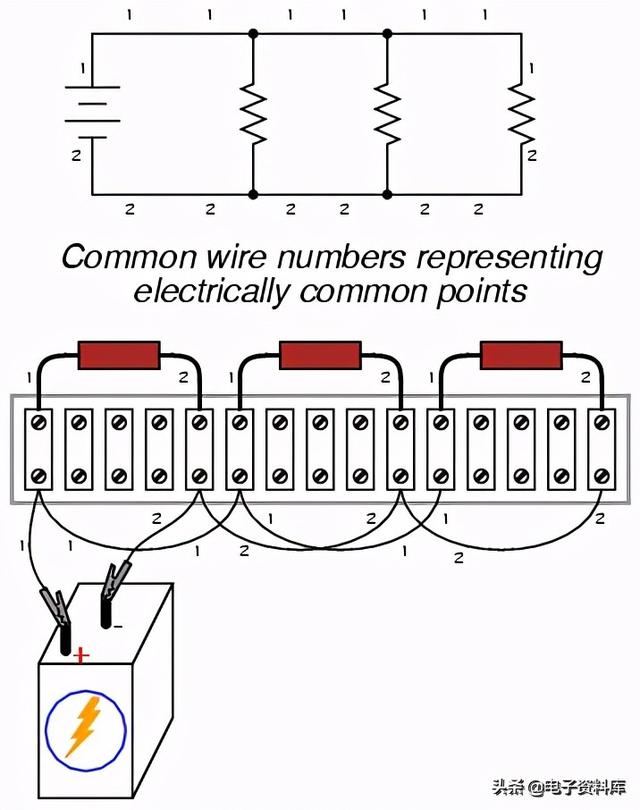
另一种工业惯例是对原理图稍作修改，以指示端子排上的实际接线点。这就要求为金属条本身设置一个标签系统：一个“TB”编号（端子排编号），然后是另一个代表金属条的编号。

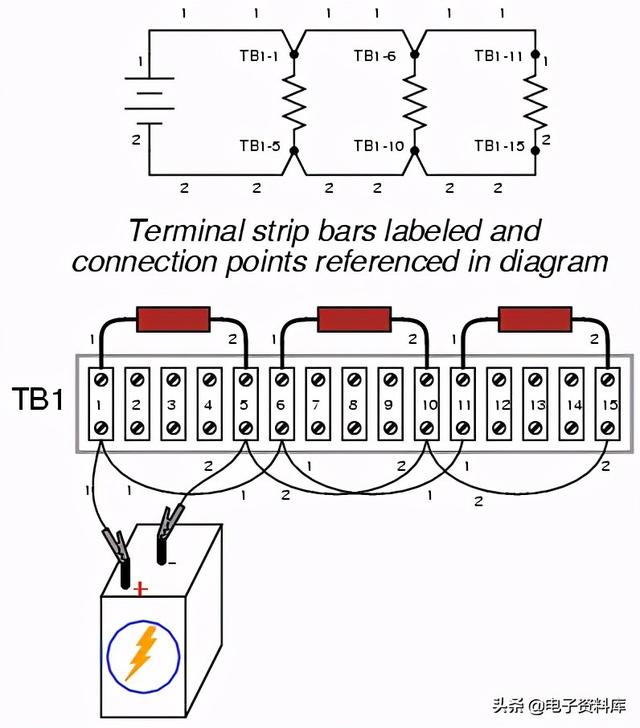
这样，原理图就可以作为一个“地图”来定位实际电路中的点，而不管连接线路在眼睛看来有多混乱和复杂。对于此处所示的简单的三电阻电路来说，这可能显得过分了，但对于大型电路的构造和维护来说，这些细节是绝对必要的，尤其是当这些电路可能跨越很大的物理距离时，使用位于多个面板或盒中的多个端子排。

• 回顾：
• A无焊试验板是一种通过将电线和元件插入塑料板上一排排孔下面的电气通用弹簧夹中，快速组装临时电路的装置。
• 焊接是一种低温焊接工艺，使用铅/锡或锡/银合金将导线和部件引线连接在一起，通常部件固定在玻璃纤维板上。
• 钢丝缠绕是焊接的一种替代方法，包括用小规格的金属丝紧紧地缠绕在元件引线上，而不是用焊接接头将元件连接在一起。
• A端子排，也称为隔离带或接线板是另一种用于安装元件和电线以构建电路的设备。固定在金属棒上的螺丝端子或重型弹簧夹为导线端部和部件引线提供连接点，这些金属棒单独安装在一块非导电材料上，如塑料、胶木或陶瓷。

,